机器人轨迹追踪控制方法

轨迹追踪控制方法

注：知识来源于哈工大《机器人力控》线上课程，网址：https://www.bilibili.com/video/BV1y7411H7fg?p=1

运动控制方程

Q = M ( q ) q ¨ + C ( q , q ˙ ) + B q ˙ + D ( q ˙ ) + G ( q ) (1) Q=M(q)\ddot q+C(q,\dot q)+B\dot q+D(\dot q)+G(q) \tag{1} Q=M(q)q¨​+C(q,q˙​)+Bq˙​+D(q˙​)+G(q)(1)

对于期望的机器人运动，需要各个关节运动的广义力 $Q$

理论上，只需要计算出所需要的驱动力，然后由驱动部件产生这样的驱动力便可以完成轨迹控制 $\to$ 实际世界中，运动参数难以无误差的得到。

广义驱动力 $Q$ 的线性化近似

Q ≈ G ( q ) + k p ( q d − q ) + k d ( q ˙ d − q ˙ ) + ∑ j = 2 N [ k j ( d ( j ) q d d t ( j ) − d ( j ) q d t ( j ) ) ] (2) Q\approx G(q)+k_p(q_d-q)+k_d(\dot q_d-\dot q)+\sum_{j=2}^N[k_j(\frac{d^{(j)}q_d}{dt^{(j)}}-\frac{d^{(j)}q}{dt^{(j)}})] \tag{2} Q≈G(q)+kp​(qd​−q)+kd​(q˙​d​−q˙​)+j=2∑N​[kj​(dt(j)d(j)qd​​−dt(j)d(j)q​)](2)

方法类似于泰勒展开，其中 q d q_d qd​ 为期望的位置矢量。

对二阶以上的导数用积分项加以近似，有：
Q ≈ G ( q ) + k p ( q d − q ) + k d ( q ˙ d − q ˙ ) + k i ∫ 0 t ( q d − q ) d t (3) Q\approx G(q)+k_p(q_d-q)+k_d(\dot q_d-\dot q)+k_i\int_0^t(q_d-q)dt \tag{3} Q≈G(q)+kp​(qd​−q)+kd​(q˙​d​−q˙​)+ki​∫0t​(qd​−q)dt(3)

PD控制器：

对于回转关节型机器人，可以简化为：
τ d ≈ G ( q ) + k p ( θ d − q ) + k d ( θ ˙ d − q ˙ ) (4) \tau_d\approx G(q)+k_p(\theta_d-q)+k_d(\dot \theta_d-\dot q) \tag{4} τd​≈G(q)+kp​(θd​−q)+kd​(θ˙d​−q˙​)(4)
而 θ d \theta_d θd​ 可以被视为常数，而且 τ d \tau_d τd​ 是理论驱动力矩，难以精确得到，进一步简化：
τ d = − k p ( θ − θ d ) − k d θ ˙ d + G ( q ) (5) \tau_d=-k_p(\theta-\theta_d)-k_d\dot \theta_d+G(q) \tag{5} τd​=−kp​(θ−θd​)−kd​θ˙d​+G(q)(5)

动态控制

C ( q , q ˙ ) → C(q,\dot q)\rightarrow C(q,q˙​)→ 离心力、科氏力在低速运动种比较小，在线性化后的误差视为扰动。
在高速运动中，该误差难以通过PID控制消除。拟采用动态控制。

动态控制：通过运动学方程得到这些非线性项（ C ( q , q ˙ ) C(q,\dot q) C(q,q˙​)）的数值，再将这些数值作为前馈或反馈。

前馈动态控制

逆动力学问题：基于参数推定值实现给定运动所需的力矩
τ I D ( q , q ˙ , q ¨ ) = M ^ ( q ) q ¨ + C ^ ( q , q ˙ ) + B ^ q ˙ + D ^ ( q ˙ ) + G ^ ( q ) (6) \tau_{ID}(q,\dot q,\ddot q)=\hat M(q)\ddot q+\hat C(q,\dot q)+\hat B\dot q+\hat D(\dot q)+\hat G(q) \tag{6} τID​(q,q˙​,q¨​)=M^(q)q¨​+C^(q,q˙​)+B^q˙​+D^(q˙​)+G^(q)(6)
其中，拥有^的参数表示为实验测定值。

控制方法：用 τ I D \tau_{ID} τID​ 替代 $\tau$
不足：模型误差、扰动的存在；一旦轨迹稍有偏差，计算力矩与实际所需力矩会有偏差，从而产生更大的轨迹误差。

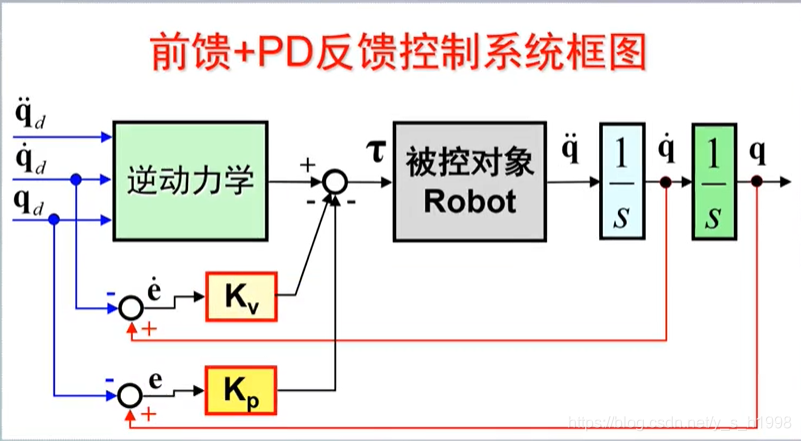
前馈+PD反馈控制

基本思想：由PD控制器控制由前馈控制得到的线性近似系统。抑制住轨迹误差和模型误差。
控制律：
τ = τ I D ( q d , q ˙ d , q ¨ d ) − K v e ˙ − K p e (7) \tau=\tau_{ID}(q_d,\dot q_d,\ddot q_d)-K_v\dot e-K_pe \tag{7} τ=τID​(qd​,q˙​d​,q¨​d​)−Kv​e˙−Kp​e(7)

计算力矩控制法

基本思想：用关节位置、速度的反馈值和期望值来估算关节加速度值。再用逆动力学求解得到所需驱动力。
τ = τ I D ( q , q ˙ , q ¨ ∗ ) q ¨ ∗ = q ¨ d − K v e ˙ − K p e (8) \tau=\tau_{ID}(q,\dot q,\ddot q^*)\\ \ddot q^*=\ddot q_d-K_v\dot e-K_pe \tag{8} τ=τID​(q,q˙​,q¨​∗)q¨​∗=q¨​d​−Kv​e˙−Kp​e(8)

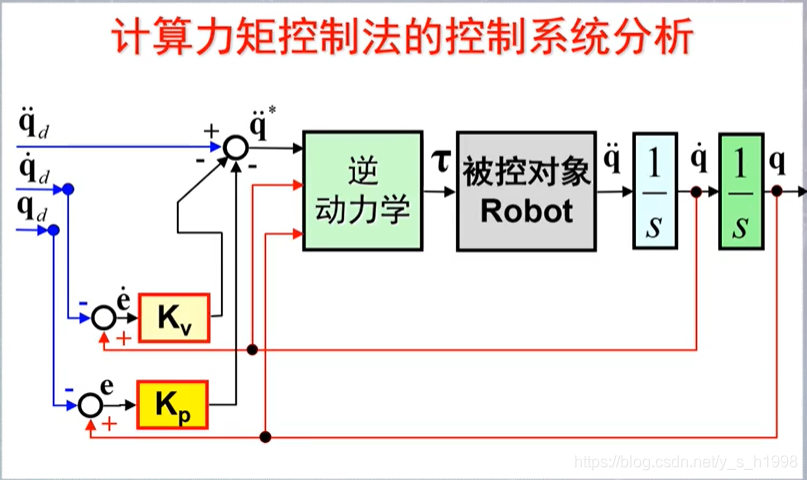
说明：逆动力学求解需要实时进行；可以适当对逆动力学方程简化，以提高计算效率；

前馈+PD反馈和计算力矩两种方法比较

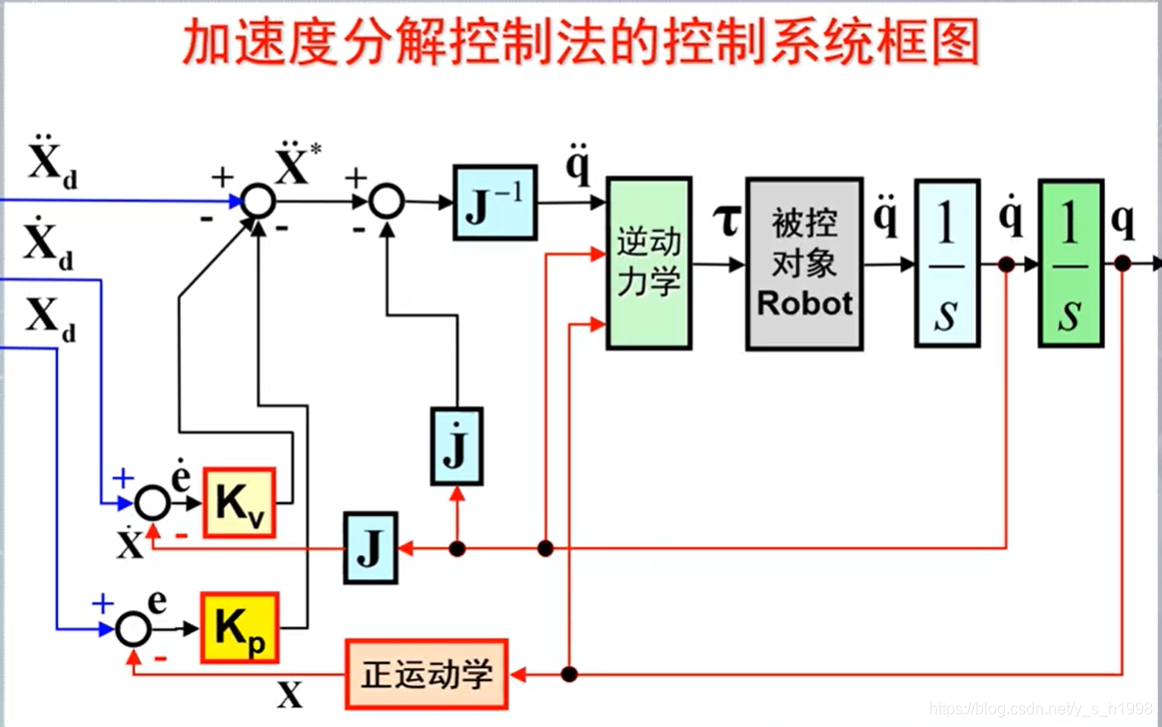
加速度分解控制法

控制思想：用关节位置、速度的反馈值和运动期望估算末端操作器的加速度值，进而得到关节加速度值，与关节速度、位置进行逆动力学计算得到驱动力。
q ¨ ∗ = J − 1 { X ¨ d + K v ( X ˙ d − X ˙ ) + K p ( X d − X ) − J ˙ q ˙ } (9) \ddot q^*=J^{-1}\lbrace \ddot X_d+K_v(\dot X_d-\dot X)+K_p(X_d-X)-\dot J\dot q \rbrace \tag{9} q¨​∗=J−1{X¨d​+Kv​(X˙d​−X˙)+Kp​(Xd​−X)−J˙q˙​}(9)
注： X ¨ = J q ¨ + J ˙ q ˙ \ddot X=J\ddot q+\dot J\dot q X¨=Jq¨​+J˙q˙​

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！