5.最后从最后一列开始求解。
//这里填你的代码^^
//实际上就是线性代数中的,把系数矩阵通过初等行变换化为最简阶梯形矩阵
#include
#include
#include
using namespace std;const int N =110;
const double eps=1e-8;
double a[N][N];
int n;int gauss()//答案存储在a[i][n]
{int c,r;//c=colmon为列,r=row为行for(c=0,r=0;cfabs(a[t][c])) t=i;if(fabs(a[t][c])=c;i--) a[r][i]/=a[r][c]; //当前行 首位变为1。注意要从最后一列开始操作for(int i=r+1;ieps)for(int j=n;j>=c;j--)a[i][j]-=a[r][j]*a[i][c];r++;}if(reps)return 2; //无解return 1;//无穷多组解}for(int i=n-1;i>=0;i--)//从最后一行计算结果,用增广矩阵那一列存储答案。for(int j=i+1;j>n;for(int i=0;i>a[i][j];int t=gauss();if(t==2) puts("No solution");else if(t==1) puts("Infinite group solutions");else{for(int i=0;i
(2)求解异或线性方程组
注意一下异或计算答案的过程。

//这里填你的代码^^
#include
using namespace std;const int N =110;
int a[N][N];
int n;int gauss()
{int r,c;for(r=0,c=0;c=0;i--)for(int j=i+1;j>n;for(int i=0;i>a[i][j];int res=gauss();if(res==1) puts("Multiple sets of solutions");else if(res==2) puts("No solution");else{for(int i=0;i
二、组合数
(1)a,b较小,求解
由于a,b较小,可以利用组合数的定义,根据根据组合数递推公式,运用递推的方式计算出a,b给定范围内的所有组合数。

等式证明:设定x为a集合中一元素,原方案数(从a个元素里面选取b个元素)等价于:不选x元素,从剩下的所有元素里面选取b个元素,加上选取x元素,从剩下的数里面选取b-1个元素。
预设定 ,即可递推。代码如下:
,即可递推。代码如下:
//这里填你的代码^^
#include
#include
using namespace std;const int N =2010;
int c[N][N];
int mod=1e9+7;
void init()
{for(int i=0;i>n;while(n--){int a, b;cin>>a>>b;cout<
(2)a,b较大,求解
a,b较大,递推是不现实的。由于结果需要模上一个数,所以可考虑从组合数计算式出发,运用逆元求解。(因为a模p 除以 b模p 不等于 a/b 模p)


由于1e9+7是一个质数,因此逆元可以用费马小定理和快速幂求解。(否则需要扩展欧几里得算法)首先运用递推求出a,b范围内的数的阶乘模10^9+7的值fact,与其逆元infact。然后根据定义计算。
代码如下:
//这里填你的代码^^
#include
using namespace std;typedef long long LL;
const int N =1e5+10;
int fact[N],infact[N],mod=1e9+7;int qmi(int a,int b,int q)
{int res=1;while(b){if(b&1) res=(LL)res*a%q;b>>=1;a=(LL)a*a%q;}return res;
}int main()
{fact[0]=infact[0]=1;for(int i=1;i>n;while(n--){int a,b;cin>>a>>b;int t=(LL)fact[a]*infact[a-b]%mod *infact[b]%mod; //注意这两个modcout<
(3)a,b很大,结果模一个给定质数。
Lucas定理

其中p为质数。详细证明及解释见https://zhuanlan.zhihu.com/p/452976974。
运用Lucas定理,我们可以直接根据定义计算:
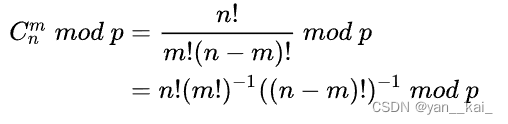
//这里填你的代码^^
#include
#include
using namespace std;
typedef long long LL;int qmi(int a, int k, int p)
{int res = 1;while (k){if (k & 1) res = (LL)res * a % p;a = (LL)a * a % p;k >>= 1;}return res;
}int c(int a,int b,int p)
{if (b>a) return 0;int res=1;for(int i=1,j=a;i<=b;i++,j--){res=(LL)res*j%p;res=(LL)res*qmi(i,p-2,p)%p;}return res;
}int lucas(LL a,LL b,int p)
{if(a>n;while(n--){LL a,b;int p;cin>>a>>b>>p;cout<
(4)高精度表示结果
如果无脑直接用高精度写需要实现阶乘、乘法、除法,过于麻烦。于是改进计算流程,只需要实现高精度乘法。
首先分解分解质因数:

质数可以使用线筛法求得。接下来只需要求出各个质数出现的次数。求法如下:
![cnt_{p} (a!)=[\frac{n}{p}]+[\frac{n}{p^{2}}]+[\frac{n}{p^{3}}]+...+[\frac{n}{p^{n}}]](https://latex.csdn.net/eq?cnt_%7Bp%7D%20%28a%21%29%3D%5B%5Cfrac%7Bn%7D%7Bp%7D%5D+%5B%5Cfrac%7Bn%7D%7Bp%5E%7B2%7D%7D%5D+%5B%5Cfrac%7Bn%7D%7Bp%5E%7B3%7D%7D%5D+...+%5B%5Cfrac%7Bn%7D%7Bp%5E%7Bn%7D%7D%5D)
即p的倍数在1到a出现的次数+p方的倍数在1到a出现的次数+······。以n=2举例:某些数是p的倍数,乘起来,则首先p的次数为这些数的个数。同时这里面又有些数是p方的倍数,于是p的次数加上p方的倍数的个数(即1*恰好只是1次方的倍数的数+2*恰好只是二次方的倍数的数)。
因此组合数 里p出现的次数:
里p出现的次数:

代码如下:
//这里填你的代码^^
#include
#include
using namespace std;
const int N =5010;
int primes[N],cnt;
bool st[N];
int sum[N];void get_primes(int n)
{for(int i=2;i<=n;i++){if(!st[i]) primes[cnt++]=i;for(int j=0;primes[j]<=n/i;j++){st[primes[j]*i]=true;if(i%primes[j]==0) break;}}
}int get(int n,int p)
{int res=0;while(n){res+=n/p;n/=p;}return res;
}vector mul(vector a,int b)
{int t=0;vector c;for (int i = 0; i < a.size(); i ++ ){t += a[i] * b;c.push_back(t % 10);t /= 10;}while(t){c.push_back(t%10);t/=10; }return c;
}int main()
{int a,b;cin>>a>>b;get_primes(a);for(int i=0;i res;res.push_back(1);for(int i=0;i=0;i--)cout<
三、卡特兰数(Catalan)
(1)定义及计算


(2)例题:

原题可抽象为一个路径选择问题:(例中取n为6)
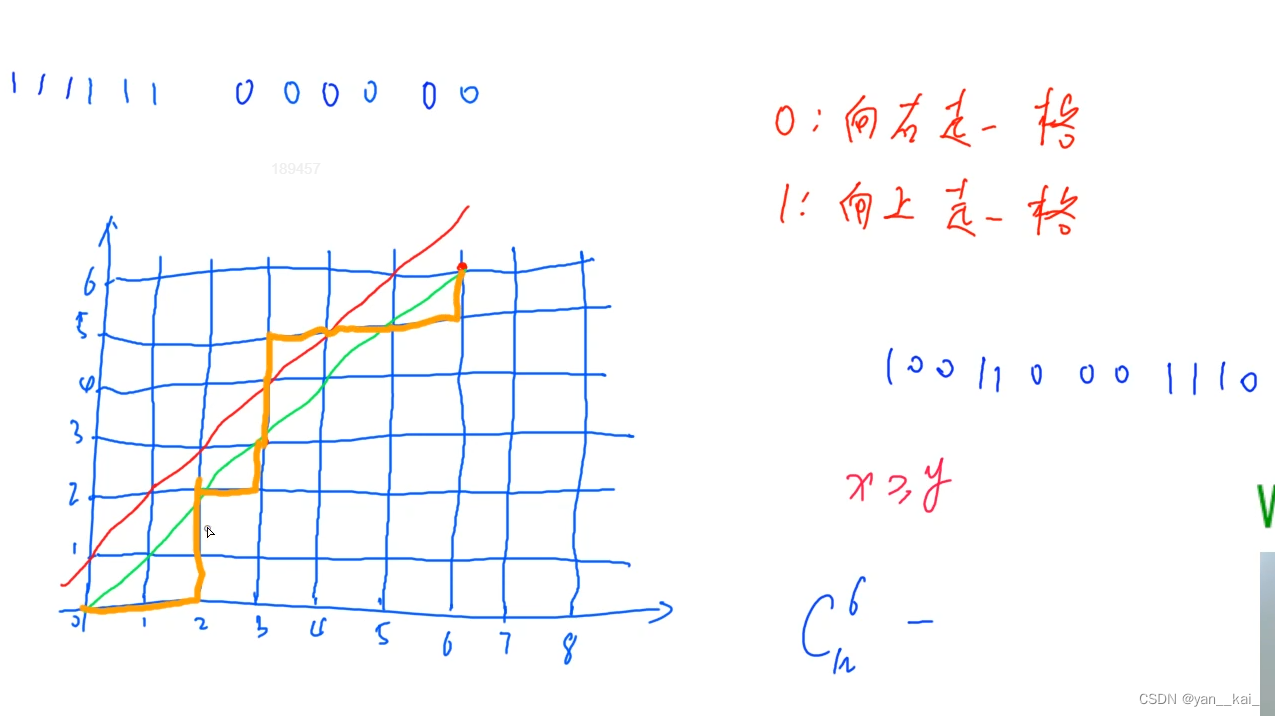
如图:0表示向右走一格,1表示向左走一格。根据题目要求,x>=y,即所选则路线不得穿过红线。回答从(0,0)走到(6,6)的走法的个数。
为求解,我们画出一条穿过红线的路径(橙线),再根据红线做其对称线,则对称线的终点为(5,7)。
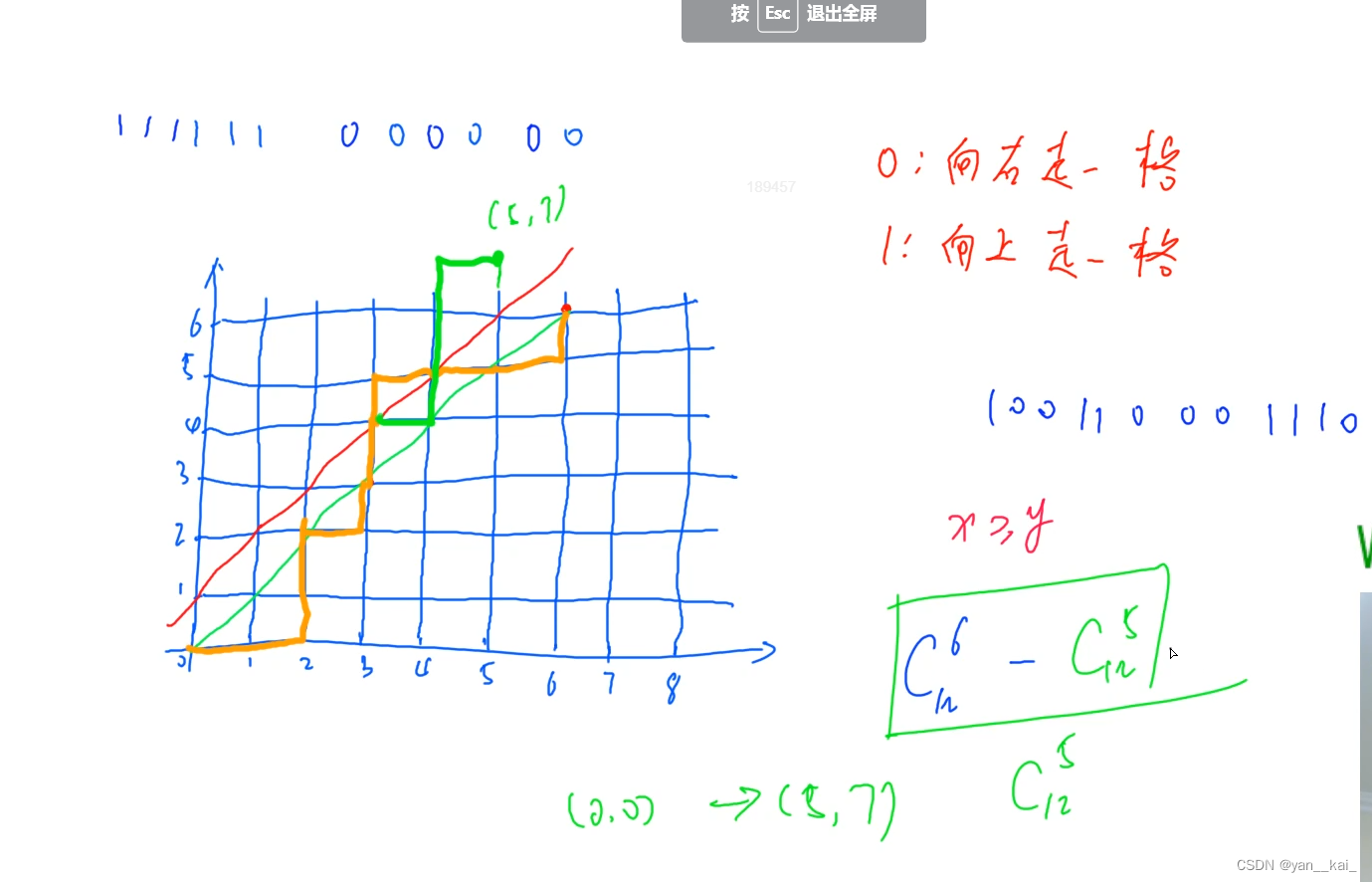
由于从(0,0)到(5,7)的路径必然经过红线,在穿过点后以红线为对称轴,做出对称线,则该对称线就是一条非法路径。同样的,每一条路径都可以一一对应一条非法路径。所有非法路径也都可以相应的对应回去。所以,有多少条从(0,0)到(5,7)的路径,就有多少条非法路径。
根据高中排列组合知识:

其通项为:

得通项则该题易解:
//这里填你的代码^^.
#include
using namespace std;
typedef long long LL;
int mod=1e9+7;
const int N =100010;int qmi(int a,int b,int p)
{int res=1;while(b){if(b&1) res=(LL)res*a%p;b>>=1;a=(LL)a*a%p;}return res;
}int main()
{int n;cin>>n;int a=2*n,b=n;int res=1;for(int i=a;i>(a-b);i--) res=(LL)res*i%mod;for(int i=1;i<=b;i++) res=(LL)res*qmi(i,mod-2,mod)%mod;res=(LL)res*qmi(n+1,mod-2,mod)%mod;cout<

,即可递推。代码如下:
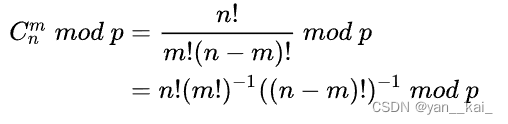
里p出现的次数:





