数学知识——高斯消元（初等行变换解方程组）代码实现

高斯消元的作用：

求解n个未知数、n个方程的方程组

 例如如下n个方程、n个未知数：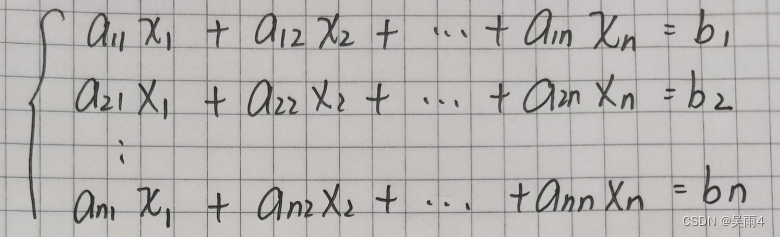

 写成n*（n+1）的矩阵：

枚举每一列

第一步：找到绝对值最大的一行

第二步：将该行换到最上面

第三步：将该行的第一个数变成1

第四步：将下面行的此列变为0

注意的是，换好了的行不需要动！

 举一个例子：

求解有三个方程、三个未知数的方程组：

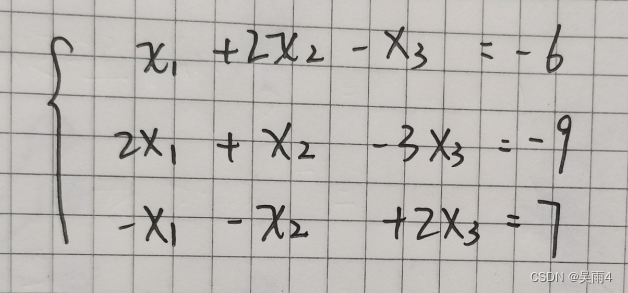
写成矩阵形式：

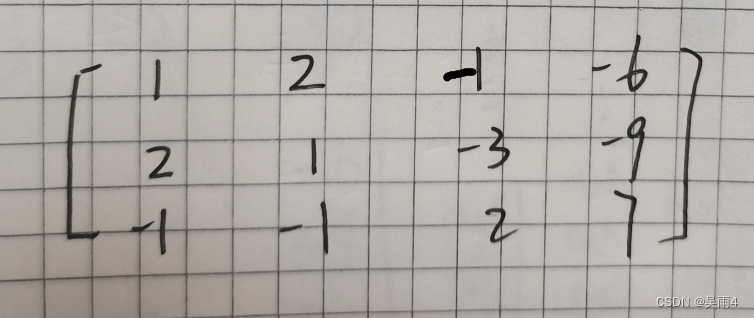
 枚举第一列，找到最大行：

 将该行换到最上面，并将该行第一个数变为1：

 将下面行的第1列都变成0：

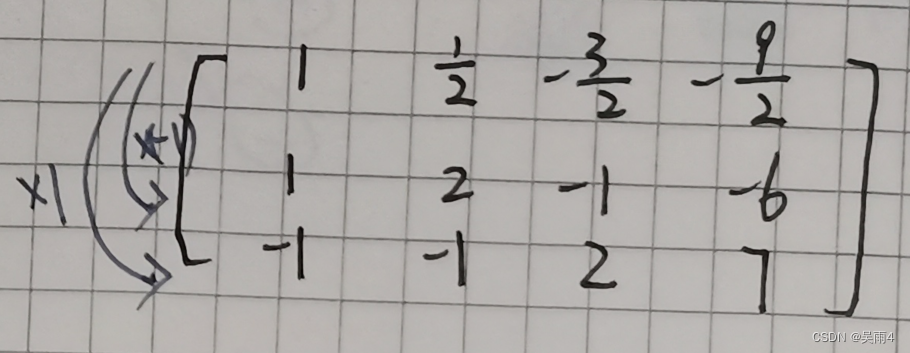
 枚举第二列，找到绝对值最大的一行，将该行的第一个数变成1：

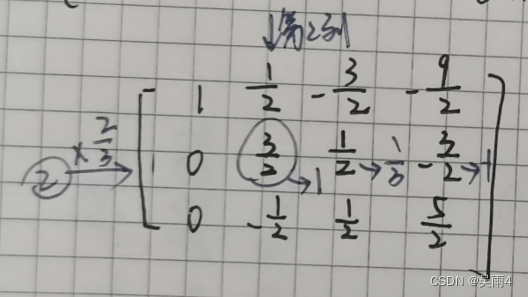
 将下面行的第1列都变成0：

 遍历第三列（由于第一行和第二行都已经改变好了，不需要动了），这里直接把第三行的第一个数变为1就行了：

 最后化简为：

由此可以依次算出：

x3=3；

x2=-2;

x1=3;

例题链接： 883. 高斯消元解线性方程组 - AcWing题库

代码（详细注释）：

#include
using namespace std;
#define IOS ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
typedef long long ll;
const int N=110;
const double eps=1e-8;
int n;
double a[N][N];
int gauss()// 高斯消元，答案存于a[i][n]中，0 <= i < n
{int c,r;//c代表列，r代表行for(c=0,r=0;cfabs(a[t][c])) t=i;if(fabs(a[t][c])=c;i--) a[r][i]/=a[r][c];//将当前行的首位变成1for(int i=r+1;ieps)for(int j=n;j>=c;j--)a[i][j]=a[i][j]-a[r][j]*a[i][c];r++;}if(reps) return 2;//无解return 1;//多解}for(int i=n-1;i>=0;i--)for(int j=i+1;j>n;for(int i=0;i>a[i][j];int t=gauss();if(t==2) cout<<"No solution"<

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！