pytorch教程龙曲良26-30
26什么是梯度1
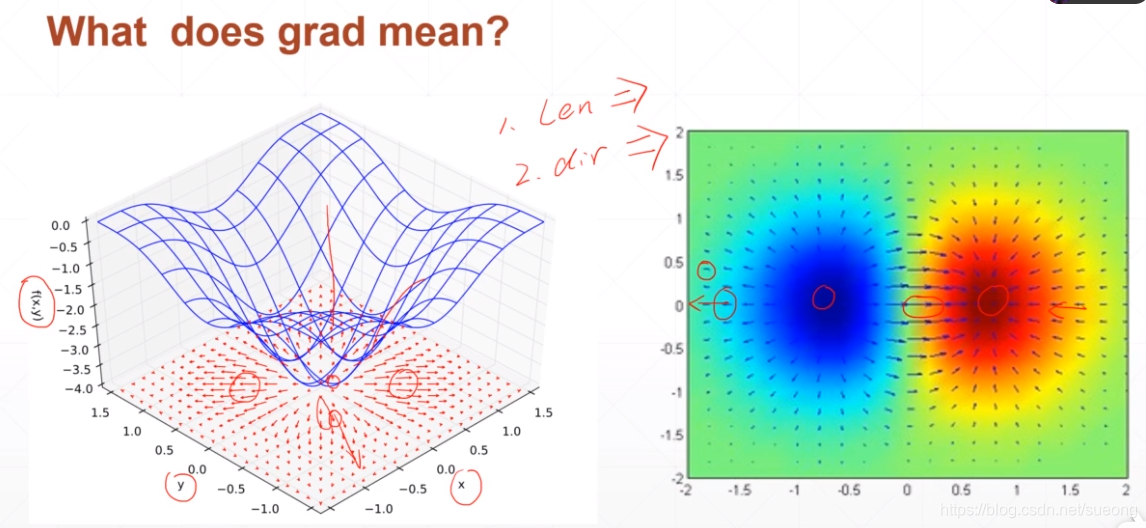
导数(在给定方向的变化量)和偏微分(在给定的自变量上的变化量)都是标量,只有大小没有方向
梯度就是所有偏微分的向量,有方向有大小

函数梯度是一个向量,向量方向表示这个函数在当前点的一个增长方向,向量的模/长度表示增长速率
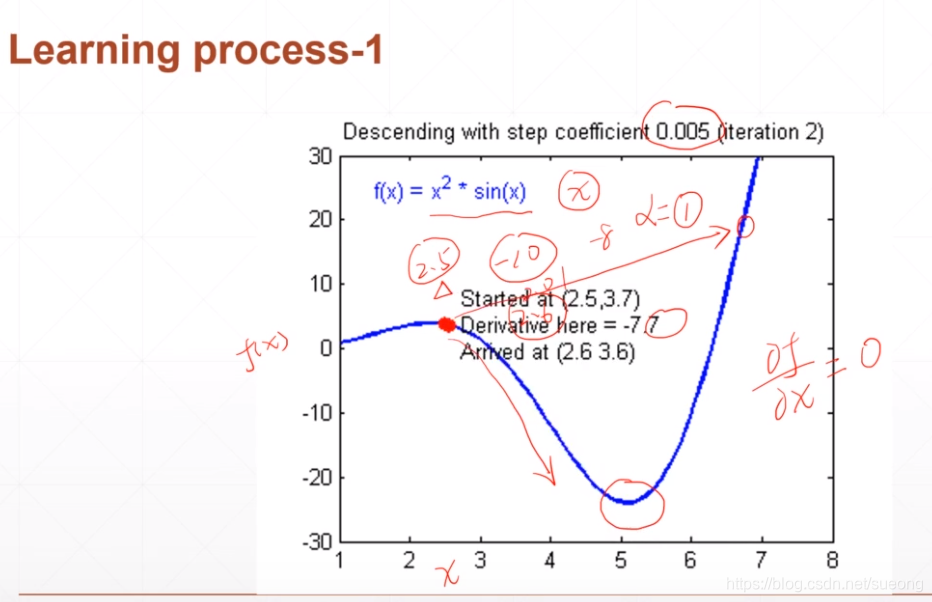
这里的a是lr,这里初始化(0,0)刚好取到极小值

当lr太大的话会更新太快跳到箭头所指的地方,显然不是我们想要的情况
27什么是梯度2
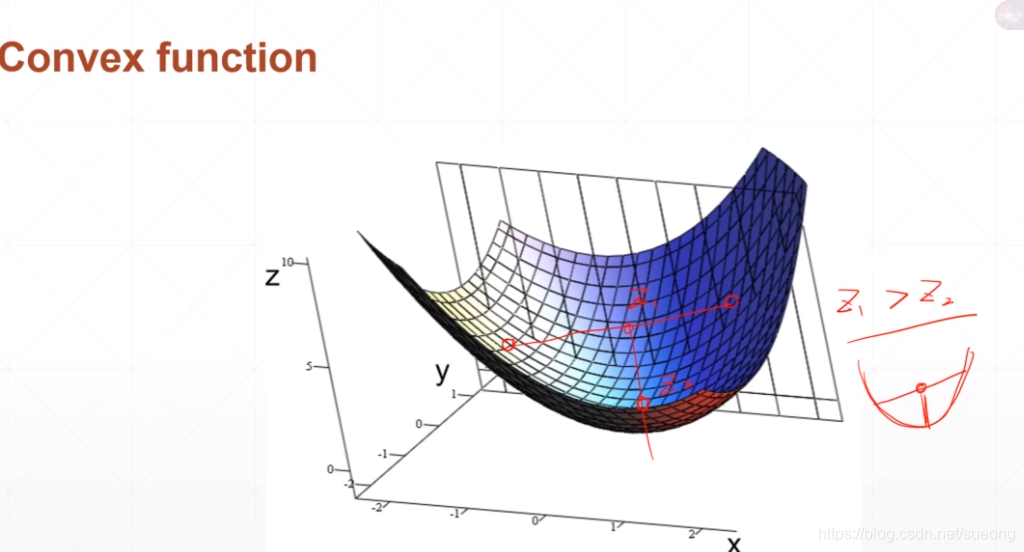
总是有z1>z2,就是凸函数(碗一样),可以找到全局最优解,但是这种情况在现实中不常见
存在多个局部最小值
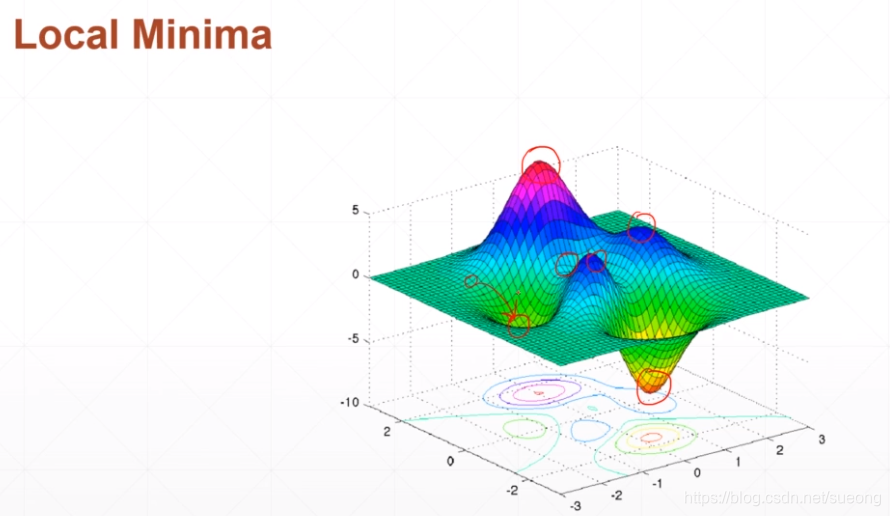
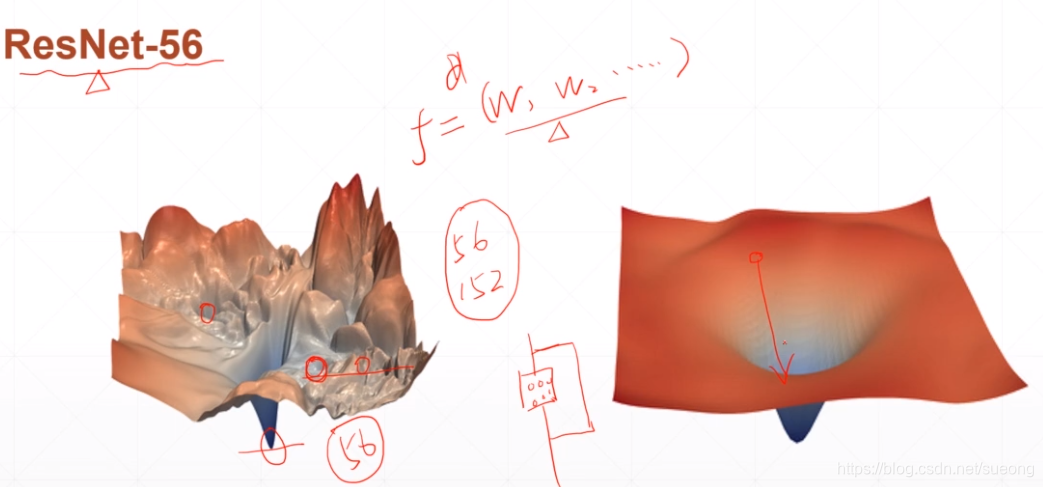
resnet56
网络很深可能平面会很粗糙陷入局部最小值,resnet56加了shortcut(走捷径)使得平面变得光滑,这样可以找到全局最小值
陷入鞍点
不是最大值也不是最小值,或者在x维度取局部最小值,在y维度上取局部最大值,比搜索到局部最小值更可怕,可能就陷在鞍点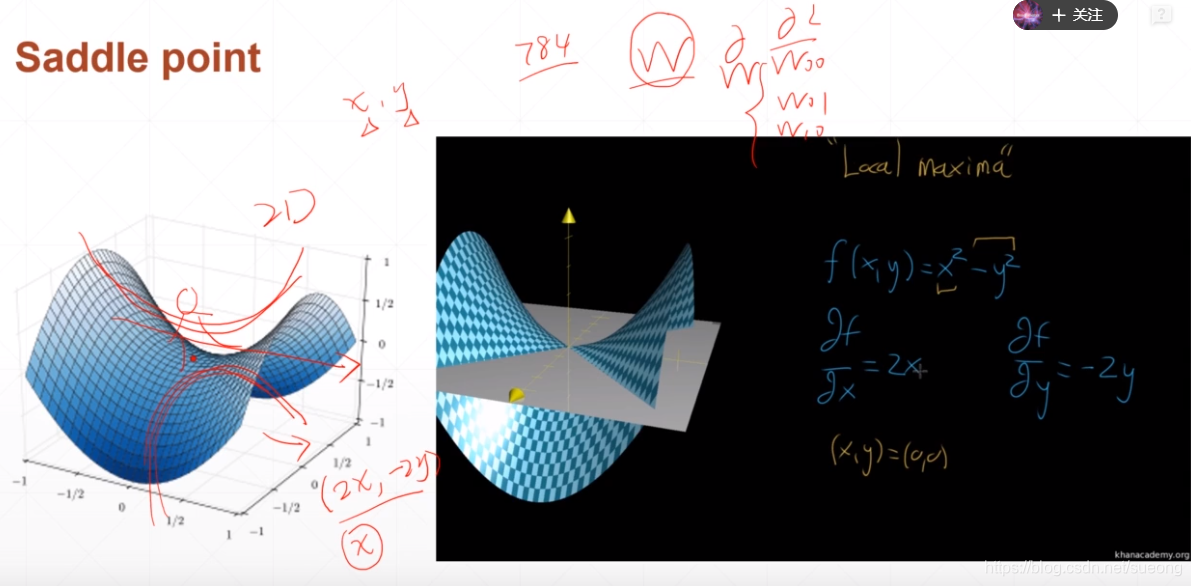
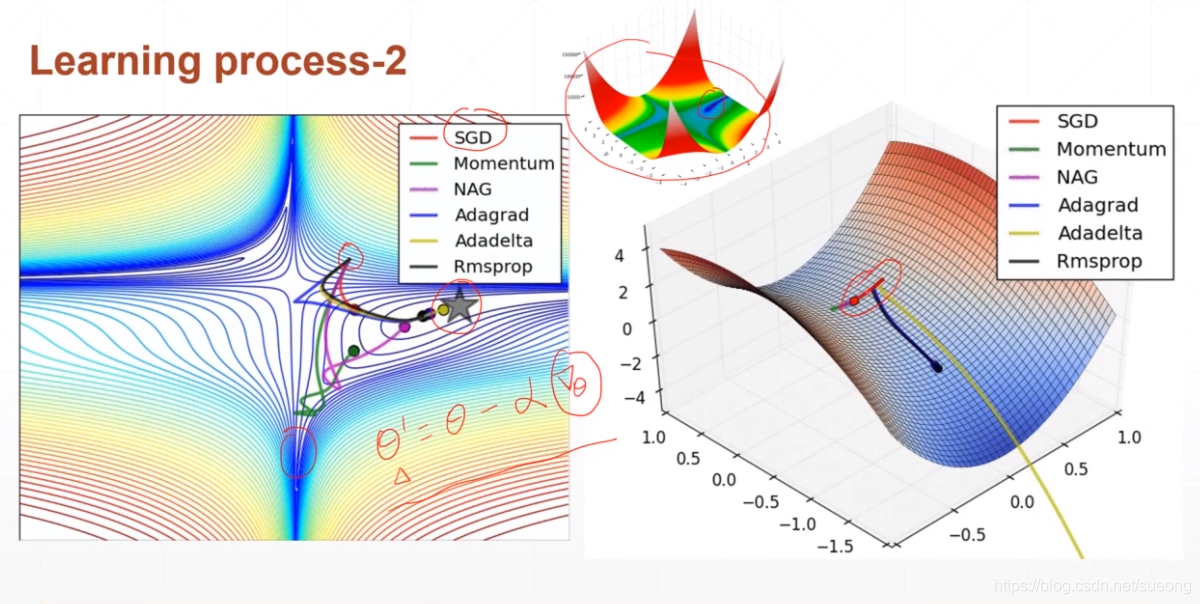
Optimizer Performance哪些因素会影响搜索全局最小值的过程
▪ initialization status
▪ learning rate
▪ momentum#动量 怎么逃离局部最小值
▪ etc.
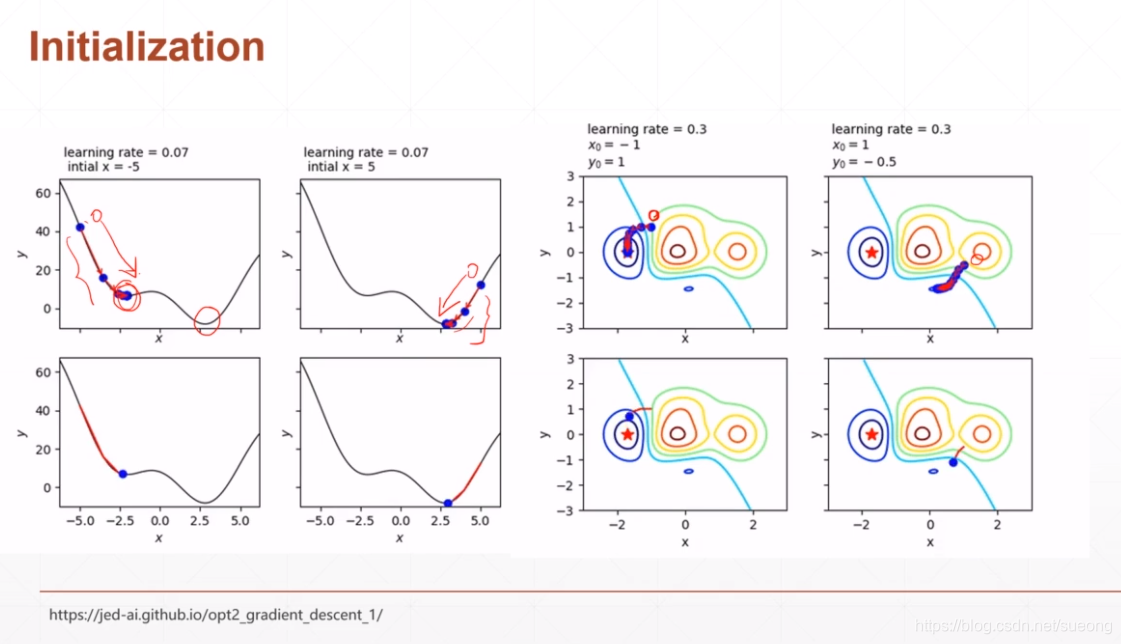
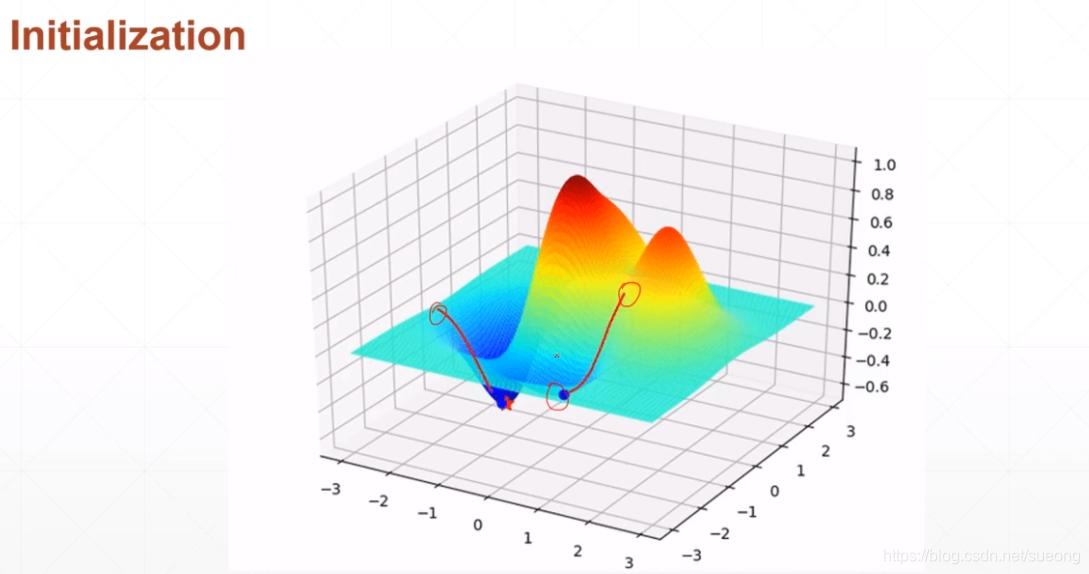
initialization status
图一初始状态从左边开始,找到局部最小值;
初始状态从右边开始,找到全局最小值,而且二者搜索的步数也不同
初始化可以按照主流的初始化方法,何恺明初始方法
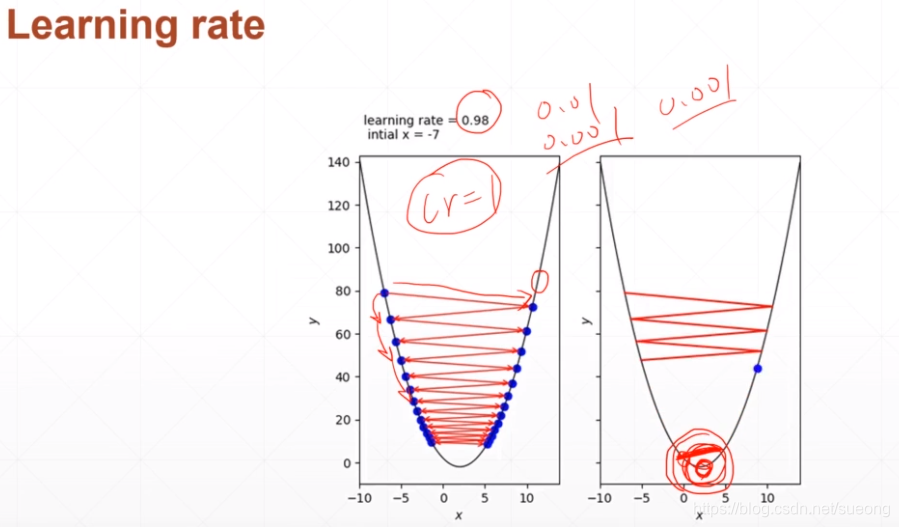
learning rate
lr太大 ,即步长太大可能会直接跨过最小值跨到另一边去,这样可能不收敛,所以lr要设置小一点,0.01,0.001,如果收敛可以大一点这样收敛速度快一点。lr不仅影响速度还影响精度,lr过大可能会使得在最小值附近震荡,不能达到最小值,所以应该设置再小一点
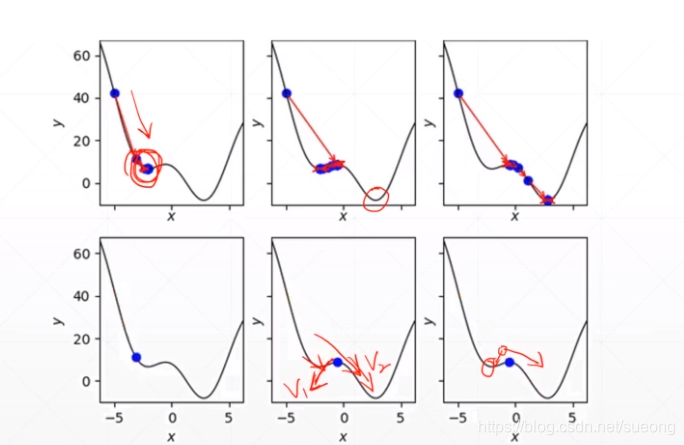
momentum
逃出局部最小值
可能会在一个小坑里徘徊但是如果惯性够大就可以冲出去,到达更小的坑去
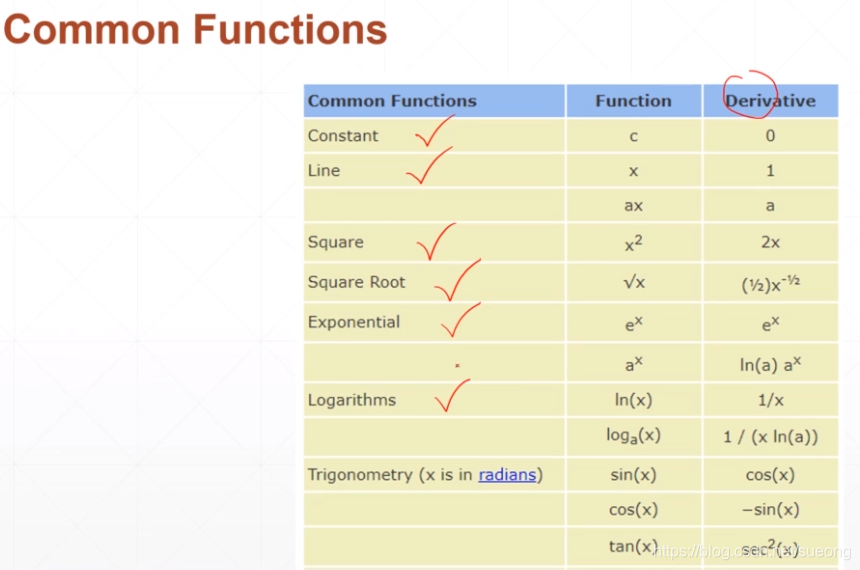
28常见函数的梯度
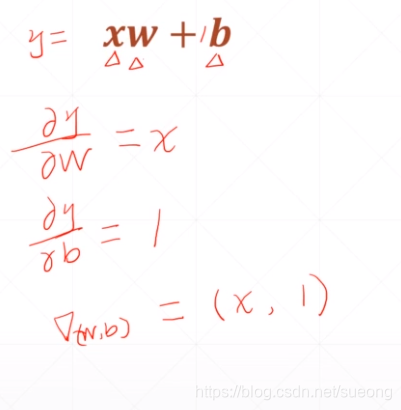
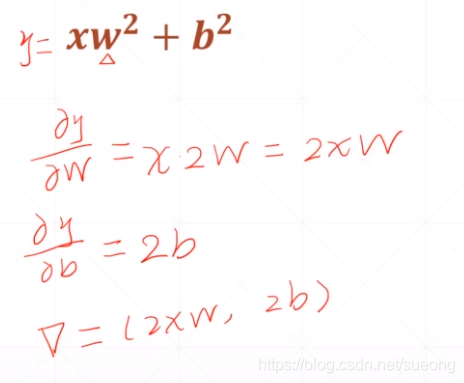
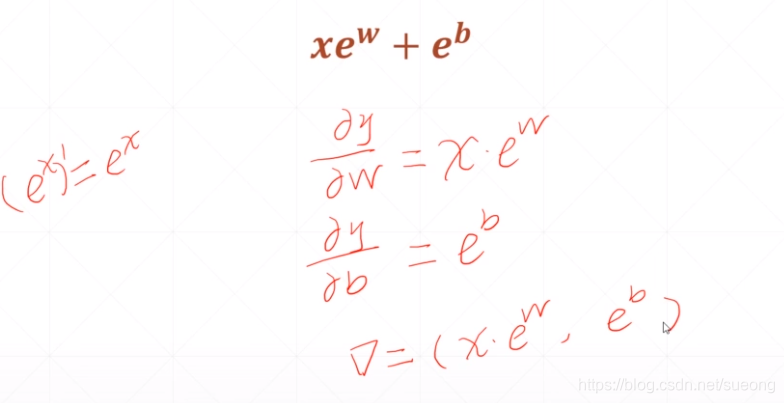
单层感知机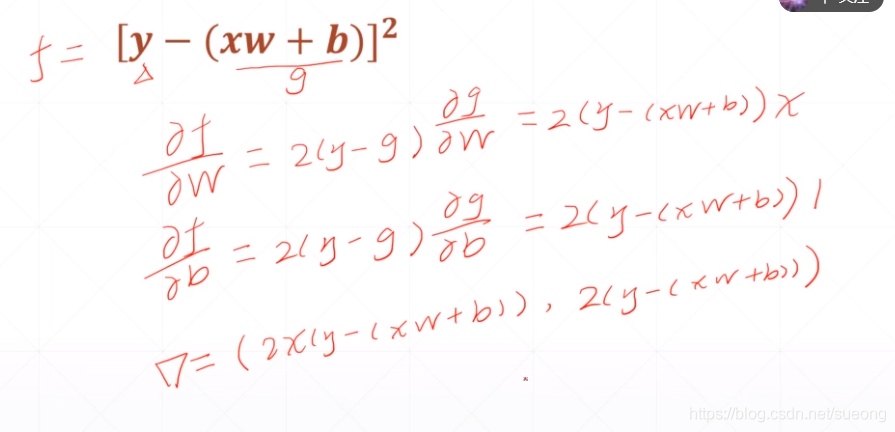
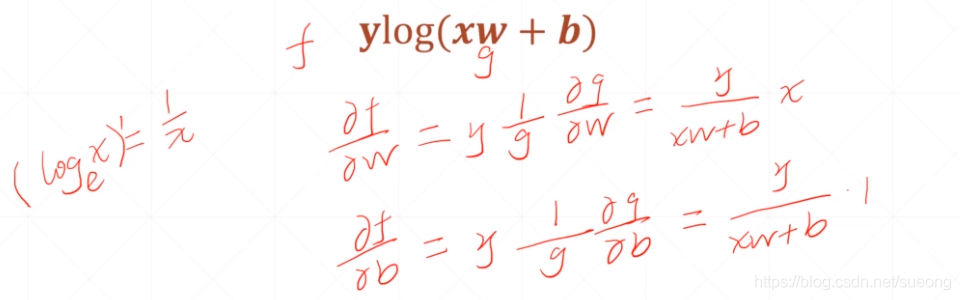
29激活函数与loss的梯度1
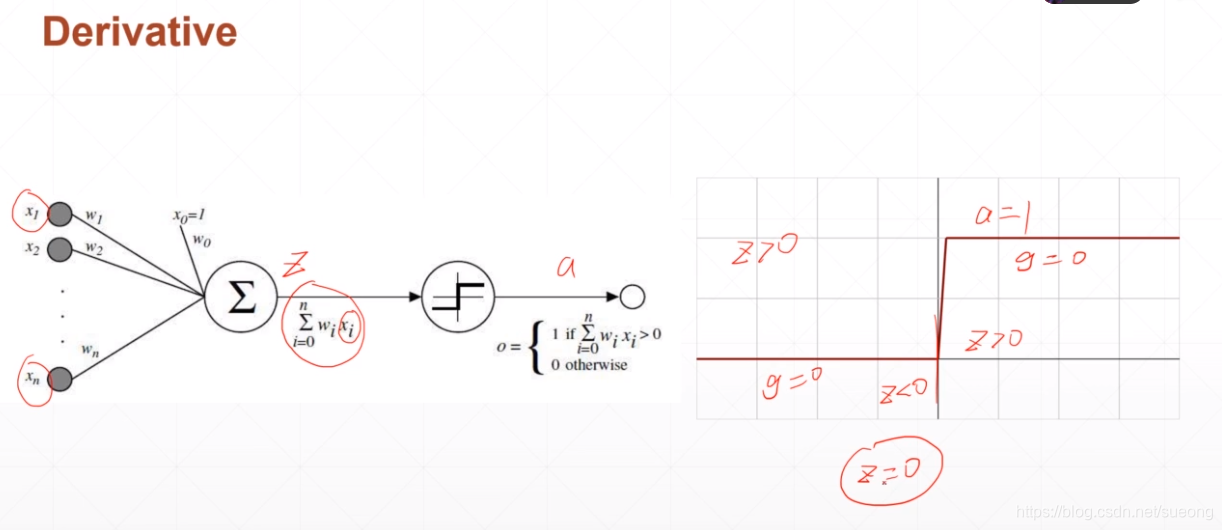
问题:单层感知机激活函数不可导
sigmoid/logistic
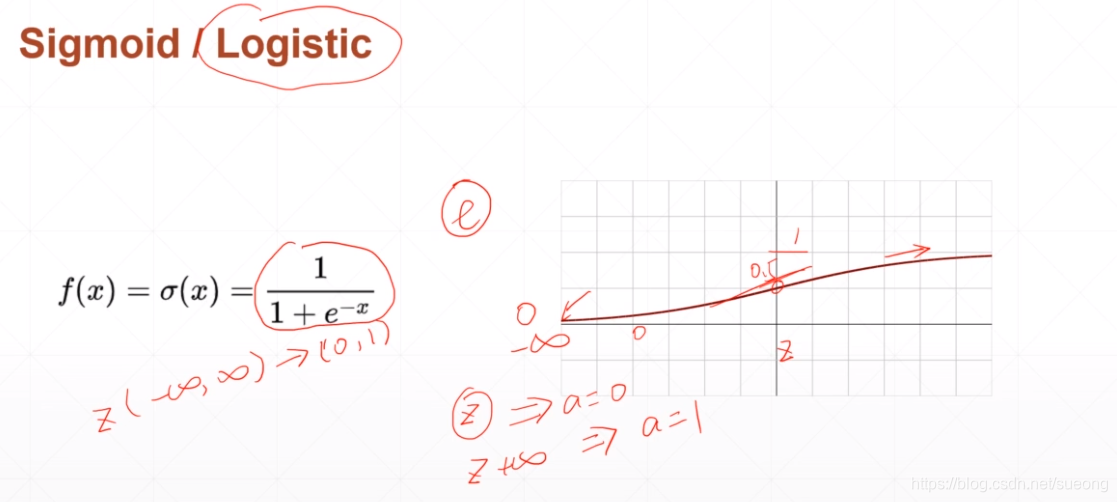
sigmoid函数的求导,可以求出一个其对x的导数,且其连续光滑,把负无穷到正无穷的值压缩在0-1之间,如概率和RGB像素点。问题是:趋向正无穷,导数接近于0,loss的值长时间得不到更新,梯度离散。

torch.nn.function as F

Tanh[-1,1]
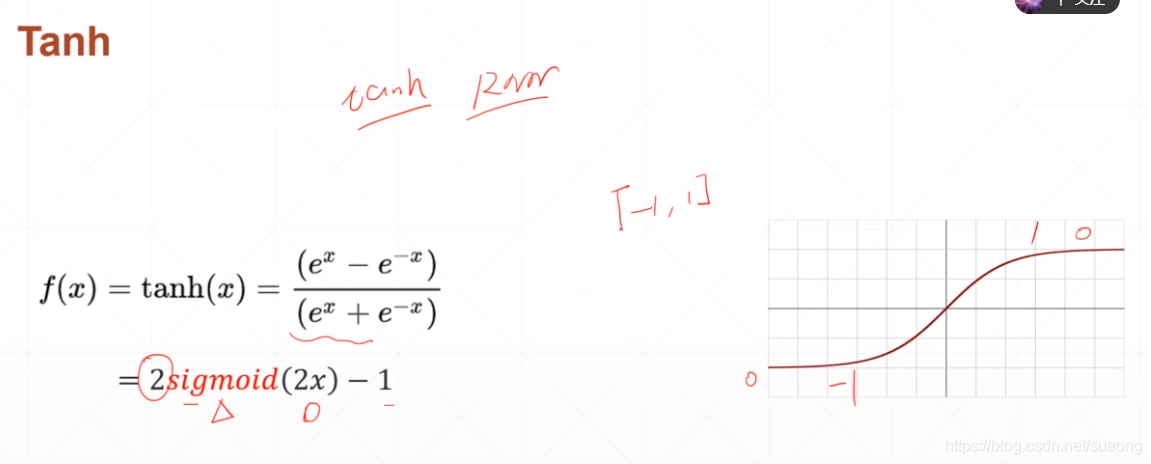
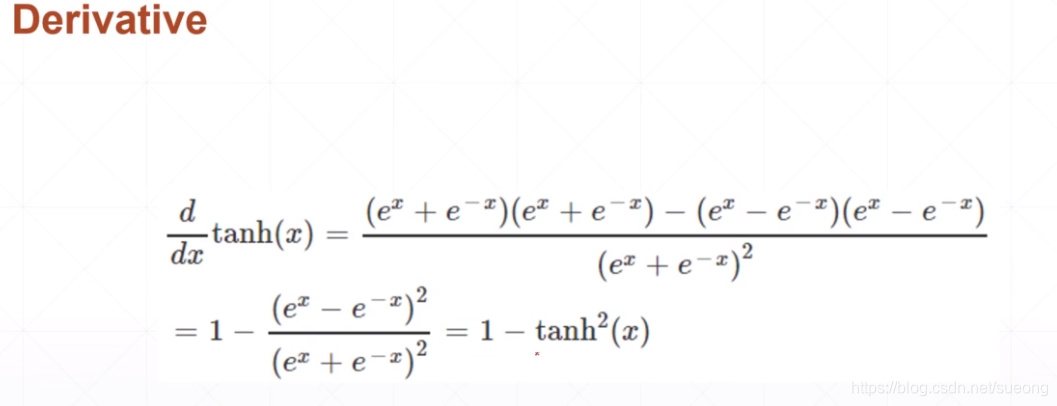

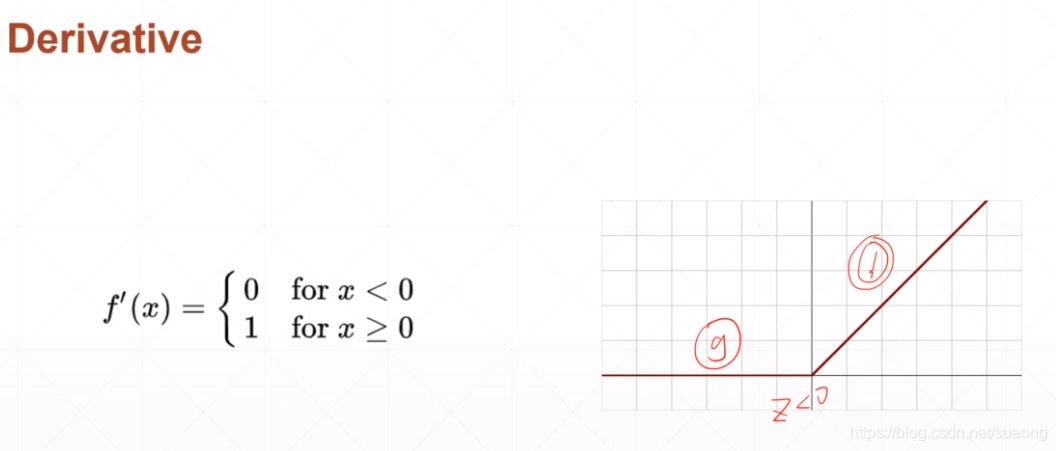
Relu
非常适合做deep learning,所以都优先使用relu函数
因为x>0 梯度是1
保持梯度不变,减少出现梯度离散或梯度爆炸的情况
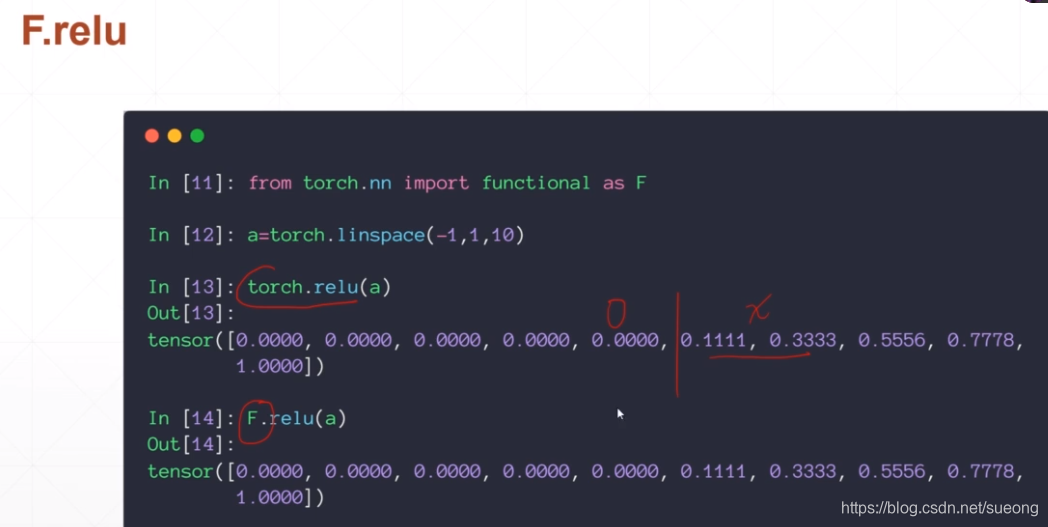
30激活函数与loss的梯度2
Typical Loss
▪ Mean Squared Error
▪ Cross Entropy Loss
▪ binary
▪ multi-class
▪ +softmax
▪ Leave it to Logistic Regression Part
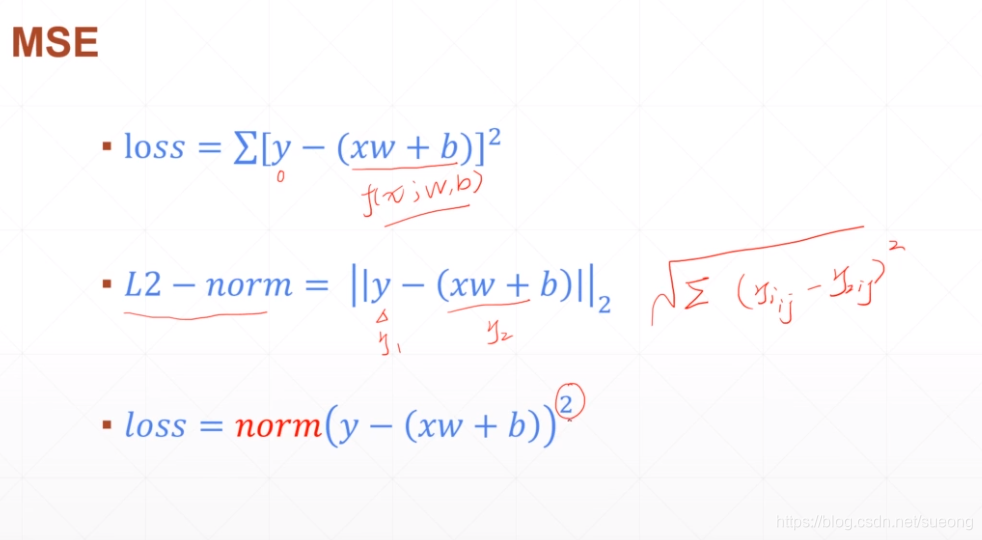
如果使用torch.norm的函数要要这样使用(因为其默认是L2-norm,有开方),要加一个平方:torch.norm(y-pred,2).pow(2)
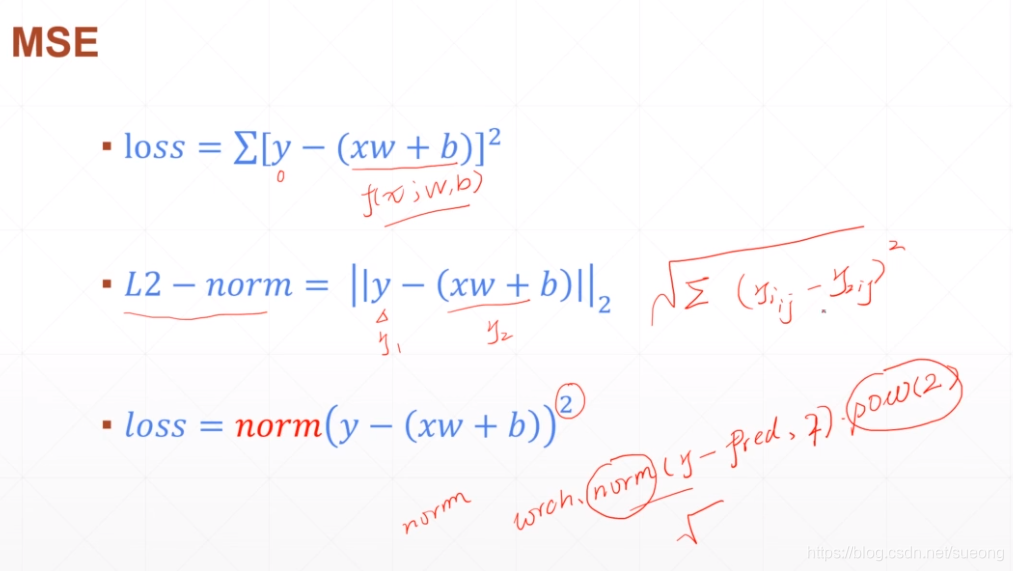

w初始化为一个长度为1 ,维度为1,值为2的一个tensor
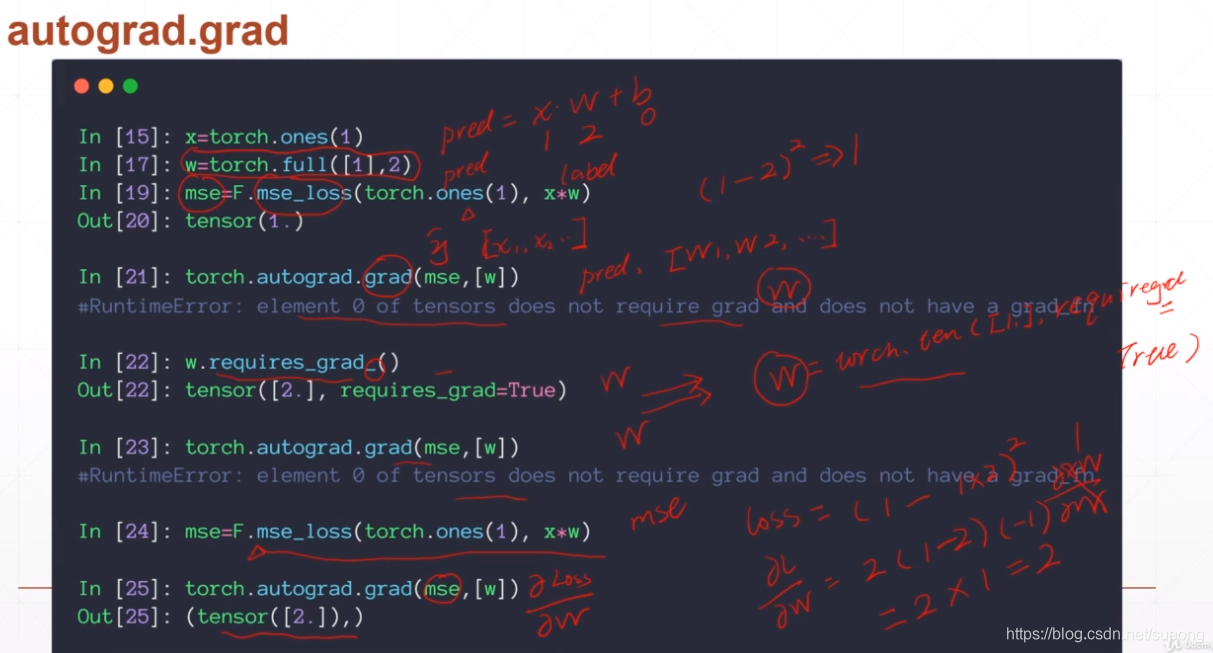
import torch
import torch.nn.functional as F
x=torch.ones(1)#标量
#w=torch.full([1],2)#长度为1且维度为1的张量 这样写默认w不需要求梯度
w=torch.tensor([2.0],requires_grad=True)
mse=F.mse_loss(torch.ones(1),x*w)#pred初始化为1
#loss=(pred-y)**2对这个函数的投递求导, 即2(pred-y)*loss对w的求导,即2(pred-y)x(-1)
#x=1 w=2,所以求导结果2(1-1*2)*1*(-1)=2
b=torch.autograd.grad(mse,[w])
print(b)#(tensor([2.]),)
backward会记录这个图的所有路径,在最后结点调用backward会自动的从后往前传播,完成这条路上所有需要梯度的计算,会把这些梯度信息附加每个tensor的成员.grad上 如w.grad和b.grad
注意要区分w.norm()还是w.grad.norm()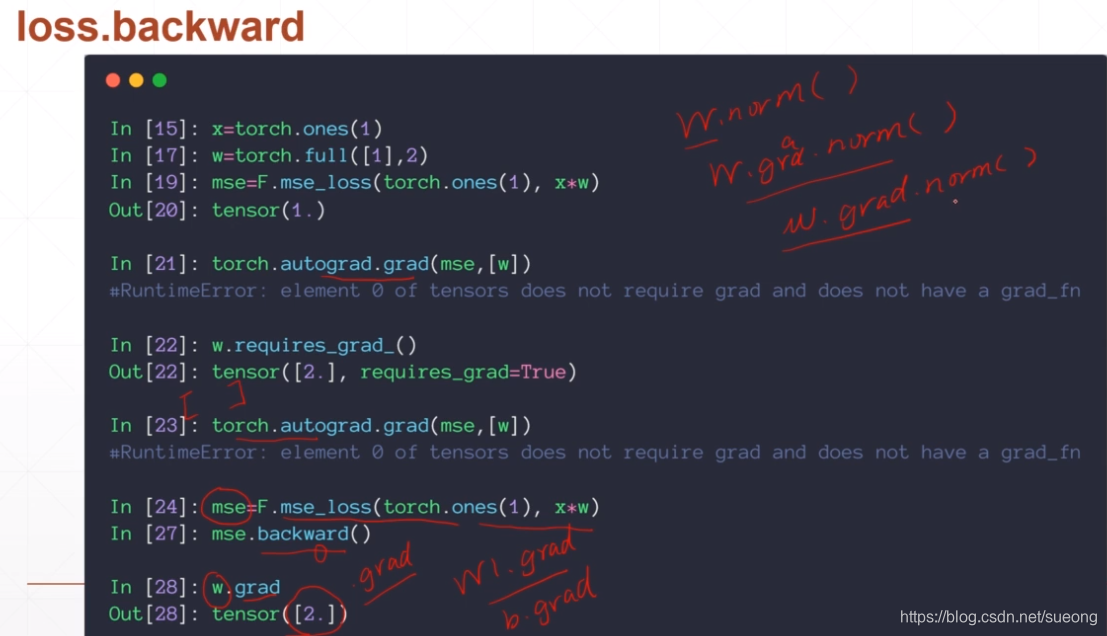
torch.autograd.grad()返回的是各个w的梯度的列表
loss.backward() 可是直接指定wi.grad

本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!