1.基本知识概念

等价类与并查集。如果用符号“=”表示集合上的等价关系，那么对于该集合中的任意对象x,y,z，下列性质成立 ：
自反性：x=x(即等于自身)
对称性：若x=y，则y=x
传递性：若x=y且y=z，则x=z
一个集合S中的所有对象可以通过等价关系划分为若干个互不相交的子集S1,S2,S3,…,它们的并集就是S，这些子集即为等价类。
确定等价类的方法：
第一步：读入并储存所有的等价对（i，j）；
第二步：标记和输出所有的等价类。

2.解决步骤分析：

假定给定集合：S={0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11};
及以下等价对：
①0=4
②3=1
③6=10
④8=9
⑤7=4
⑥6=8
⑦3=5
⑧2=11
⑨11=0
我们以等式左边的值为根，最后一棵树是一个等价类，如果两个结点的根节点相同，就是在一个等价类。
如下解决过程：

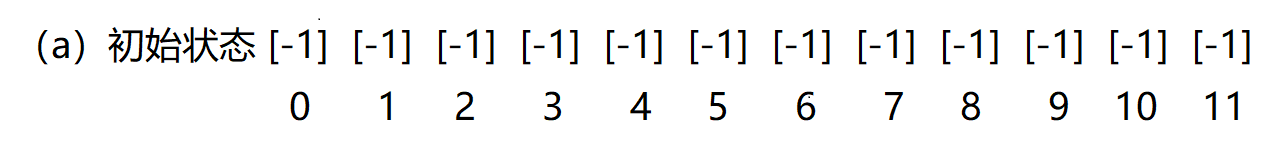
如下图，黑色的为单个等价类，其他颜色相同的为一个等价类，我们以等号左边的作为根：

处理完⑤-⑧后的结果 ：

处理完⑨后的结果 ：

3.解决代码：

3.1正常普通解决代码：

class UFsets
{
private:int* parent;unsigned int size;
public:UFsets(unsigned int sz){size = sz;parent = (int*)malloc(sizeof(int) * sz);for (int i = 0; i < size; i++){parent[i] = -1;}}~UFsets(){free(parent);}bool Union(int a, int b){bool res = false;int ra = FindParent(a);int rb = FindParent(b);if (ra != rb){parent[ra] += parent[rb];parent[rb] = ra;res = true;}return res;}int FindParent(int ra){while (parent[ra] >= 0){ra = parent[ra];}return ra;}void Print(int ri){printf("%3d ", ri);for (int i = 0; i < size; i++){if (parent[i] == ri){Print(i);}}}void PrintSet(){int s = 0;for (int i = 0; i < size; i++){if (parent[i] < 0){printf("第 %d 集合\n", ++s);Print(i);printf("\n");}}}
};int main()
{UFsets set(12);set.Union(0, 4);set.Union(3, 1);set.Union(6, 10);set.Union(8, 9);set.Union(7, 4);set.Union(6, 8);set.Union(3, 5);set.Union(2, 11);set.Union(11, 0);return 0;
}

调试查看parent值发现和我们分析时最后的数组结果一样（我统一以等价左边的值作为根）：

用类的PrintSet()打印各个等价类结果：

4.加权规则和折叠规则

但是Find和Union的操作性能不好。假设最初n个元素构成n棵树组成的森林，parent[i] = -1。做处理Union(n-2,n-1),Union(n-3,n-1),Union(n-4,n-1)…Union(0，n-1)后，将产生如下图所示的退化的树：

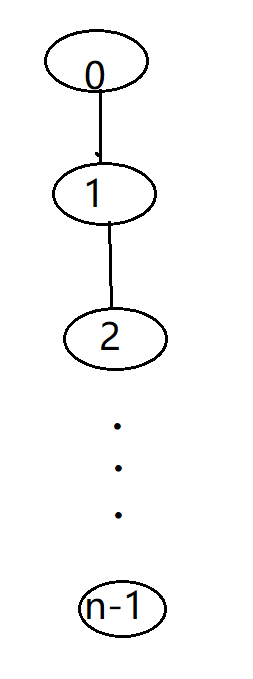
执行一次Union操作需时间O(1)，n-1此是O(n)。若再执行Find(0),Find(1),…,Find(n-1)，若被搜索的元素为i，完成Find(i)操作为O(i)，完成n次搜索是O(n^2)。
所以在这里提出了加权规则和折叠规则。

4.1加权规则

先判断两个集合中的结点个数，如果以i为根的树中的结点个数少于以j为根的树中的结点个数，即parent[i] > parent[j]，则让j成为i的双亲，否则，让i成为j的双亲。以下即为加权规则代码吗，将以下代码添加到class UFsets中即可。

bool WeightedUnion(int a, int b)//加权规则{bool res = false;int ra = FindParent(a);int rb = FindParent(b);if (ra != rb){if (parent[ra] > parent[rb])//说明parent[rb]结点更多，让rb成为根节点{parent[rb] += parent[ra];parent[ra] = rb;}else//让ra成为根节点{parent[ra] += parent[rb];parent[rb] = ra;}res = true;}return res;}

4.2折叠规则

如果j是从i到根的路径上的一个结点，并且parent[j] ≠ root，则把parent[i]置于root，意思是让i的双亲直接为root。
如下即为从i结点向上压缩路径，将代码添加到class UFsets中即可 ：

//折叠规则压缩路径void Coollapsingfind(int i){int j = i;while (parent[j] >= 0)//寻找树的根节点{j = parent[j];}while (i != j){int tmp = parent[i];parent[i] = j;i = tmp;}}

以下为折叠压缩后的结果：

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！