[算法笔记] 爬楼梯
70.爬楼梯 https://leetcode-cn.com/problems/climbing-stairs/
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
注意:给定 n 是一个正整数。
示例 1:
输入: 2 输出: 2 解释: 有两种方法可以爬到楼顶。 1. 1 阶 + 1 阶 2. 2 阶
示例 2:
输入: 3 输出: 3 解释: 有三种方法可以爬到楼顶。 1. 1 阶 + 1 阶 + 1 阶 2. 1 阶 + 2 阶 3. 2 阶 + 1 阶
You are climbing a stair case. It takes n steps to reach to the top.
Each time you can either climb 1 or 2 steps. In how many distinct ways can you climb to the top?
Example 1:
Input: 2 Output: 2 Explanation: There are two ways to climb to the top. 1. 1 step + 1 step 2. 2 steps
Example 2:
Input: 3 Output: 3 Explanation: There are three ways to climb to the top. 1. 1 step + 1 step + 1 step 2. 1 step + 2 steps 3. 2 steps + 1 step
Constraints:
1 <= n <= 45
题解:
1. 动态规划法求解:
本问题其实常规解法可以分成多个子问题,爬第n阶楼梯的方法数量,等于 2 部分之和:a. 爬上` n-1` 阶楼梯的方法数量q。因为再爬1阶就能到第n阶b. 爬上` n-2` 阶楼梯的方法数量p。因为再爬2阶就能到第n阶
所以我们得到公式 r = p + q
同时需要初始化 r=1 和p=0,q=0。
注意:初始值的设置和循环条件有关系。
时间复杂度:O(n)
C语言解法:
int climbStairs(int n){int p = 0, q = 0, r = 1;for (int i = 1; i <= n; ++i) {p = q; q = r; r = p + q;}return r;
}
2. 斐波那契数列
如果观察数学规律,可知本题是斐波那契数列,那么用斐波那契数列的公式即可解决问题,公式如下:
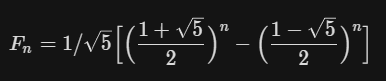
时间复杂度:O(logn)
Java实现:
class Solution {public int climbStairs(int n) {double sqrt_5 = Math.sqrt(5);double fib_n = Math.pow((1 + sqrt_5) / 2, n + 1) - Math.pow((1 - sqrt_5) / 2,n + 1);return (int)(fib_n / sqrt_5);}
}
声明:感谢画手大鹏提供的思路: https://leetcode-cn.com/problems/climbing-stairs/solution/hua-jie-suan-fa-70-pa-lou-ti-by-guanpengchn/
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!