每天一道LeetCode-----计算二叉树的最大路径和，路径只需要从一个节点到达另一个节点，无其他要求

Binary Tree Maximum Path Sum

原题链接Binary Tree Maximum Path Sum

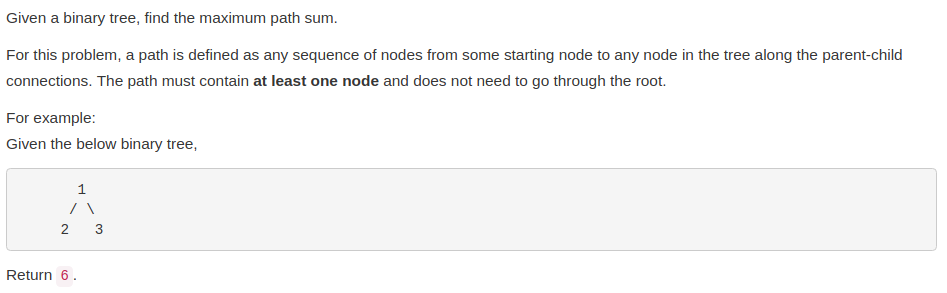
给定一个二叉树，计算二叉树中最长的路径和，路径只需要从一个节点到另一个节点，不需要经过根节点，也不需要从叶子节点开始，但至少包含一个节点

乍一看，二叉树上任意一条路径都有可能是最后的结果，而解决二叉树又必须使用递归，如果在递归的过程中计算以当前节点为根节点的子树的最长路径和，同时要求必须经过当前节点，那么在递归的过程中就可以将所有可能都遍历到

但是在递归向上返回时不能返回上述过程计算的路径和，因为返回的过程意为着路径还需要向上延伸，那么到达当前节点向上延伸，就不可能将左右两边都计算到。所以在向上返回时需要返回一条经过当前节点但是只在一侧的路径长

代码如下

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode(int x) : val(x), left(NULL), right(NULL) {}* };*/
class Solution {
public:int maxPathSum(TreeNode* root) {int maxSum = INT_MIN;maxPathSum(root, maxSum);return maxSum;}
private:/* 函数计算必须经过root的路径长，更新maxSum* 返回必须经过root，但是只包含一侧的路径长 */int maxPathSum(TreeNode* root, int& maxSum){if(!root)   return 0;/* 计算左右子树的路径长 */int leftSum = maxPathSum(root->left, maxSum);int rightSum = maxPathSum(root->right, maxSum);/* 必须经过root */int sum = root->val;/* 大于0才需要加 */sum += (leftSum > 0) ? leftSum : 0;sum += (rightSum > 0) ? rightSum : 0;/* 更新maxSum，maxSum中保存遍历到的路径和的最大值 */maxSum = std::max(maxSum, sum);/* 只能返回一侧，当然减去小的那边 */if(leftSum > 0 && rightSum > 0)return sum - std::min(leftSum, rightSum);elsereturn sum;}
};

本题还是利用递归，不过解决思路不太容易理解，需要弄清楚如何遍历所有的路径，因为路径必须有节点，所以可以计算必须经过根节点的路径和求最大值，需要注意的是递归向上返回时不可以直接返回路径和，因为向上返回意为着路径向上延伸，那必须最多只能经过当前节点的左右子树中的一个，所以需要减去较小的子树

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！