bp神经网络代码_精通数据科学笔记 神经网络

本章讨论一种全新的建模理念，它不关心模型的假设以及相应的数学推导，也就是说不关心模型的可解释性，其核心内容是模型实现，虽然到目前为止，人们还无法理解，但在某些特定场景里预测效果却非常好。我们把这种模型称为神经网络，深度学习，人工智能等。

神经元

​

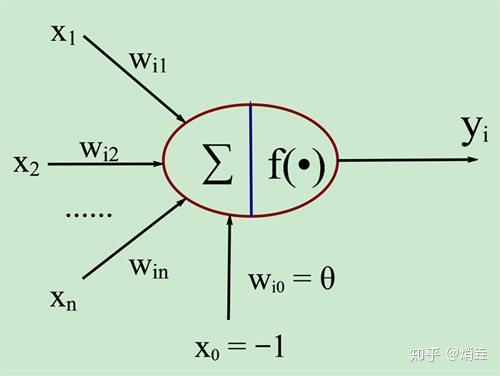
模型的输入是数据里的自变量

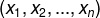
接收输入变量的是一个线性模型

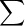
接下来是一个非线性激活函数

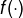
，这是神经元模型的核心，常用的激活函数有很多，如sigmoid,ReLU,tanh,maxout等

模型各部分联结起来得到输出

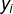
，传递给下一个神经元

sigmoid 神经元与二元逻辑回归

sigmoid 函数作为神经元激活函数的两个好处：

实用：能将任意实数映射到(0,1)区间

理论：模拟了两种效应的竞争关系，可近似表达正效应大于负效应的概率

当模型被用于二元分类时，sigmoid神经元模型就是逻辑回归

softmax 函数与多元逻辑回归

独热编码：对于k元分类问题，用一个k维行向量来表示它的类别

Softmax 函数：给定输入数据，输出这个数据的类别概率

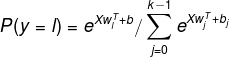
（softmax 函数）

对于k元逻辑回归，某个数据点的损失可以写成softmax函数与行向量的乘积形式

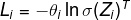
其中

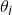
是独热编码向量，

，

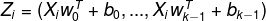
是Softmax函数

神经网络

​

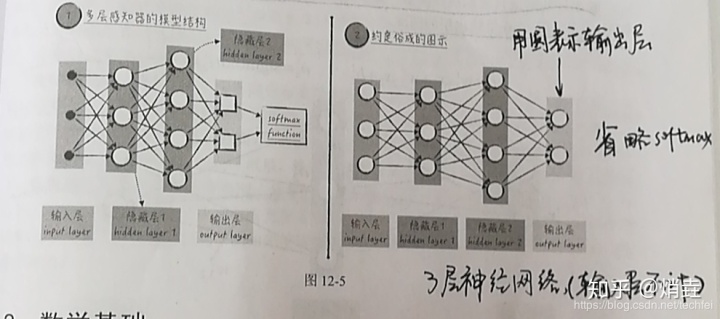
神经元按层组织，每一层包含若干神经元，层内神经元相互独立，但相邻两层之间是全连接的

神经网络不同层按功能分为3类，分别是输入层，隐藏层，和输出层。

隐藏层里每一个圆圈包含线性模型和激活函数，统称神经元

输入层不对数据做处理

输出层只包含线性模型，没有激活函数

代码实现

借助第三方库tensorflow实现

​

反向传播算法(BP)

反向传播算法是神经网络的基石，但其本身却饱受质疑，因为没有生物学的支持，违背神经网络的建模理念，BP算法的核心是利用链式法则计算多元函数偏导数

计算的起点：

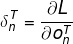
反向传播：

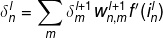
模型训练梯度：

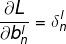
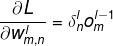
BP算法和最大期望EM算法类似，可分为向前计算和向后计算

• 首先随机生成模型参数

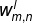
和

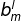
• 根据现有的模型参数和训练数据，计算每个神经元的

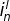
和

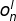
• 根据随机梯度下降法更新参数

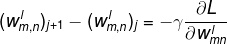
提高神经网络的学习效率

改进激活函数

学习效率正比于激活函数的导数

sigmoid函数：非0中心；自变量远离0时导数接近0

tanh函数：以0为中心但是自变量远离0时导数接近0

ReLU函数:自变量小于0时，导数恒小于0，自变量大于0时，导数恒大于0

参数初始化：令

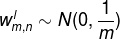
，其中m是上一层神经元个数，可以提高学习效率

梯度消失和梯度爆炸是同一个问题的两个极端，是神经网络的权重项叠加效应导致。

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！