双边z变换公式_光通信与数学 傅里叶变换

Mathematics->Fourier transform非完备性证明，逻辑自洽，深入浅出，构建光通信数学观。

光通信与数学 - 基础1

光通信与数学 - 泰勒展开式与欧拉公式

光通信与数学 - 傅里叶级数(实数域)

光通信与数学 - 傅里叶级数(复指数域)

f(ε)表达式称为傅里叶变换，亦称频谱，频率ε的单位为赫兹。

s(x)表达式称为傅里叶逆变换。

f(ε)与s(x)一起称为傅里叶变换对。

角频率形态

角频率ω=2πε(以弧度/秒为单位)，代入傅里叶变换对

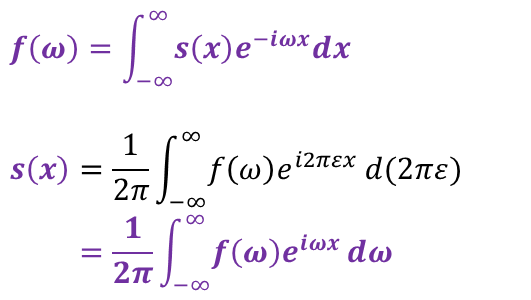
非周期矩形函数的傅里叶变换

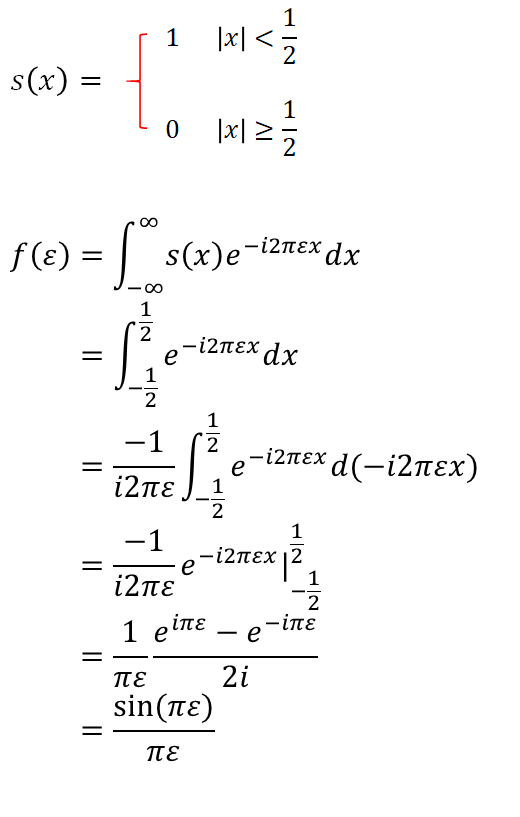
对于非周期的矩形函数，其傅里叶变换为连续的曲线，说明其频率分量为连续的，且每个频率分量值都是实数值，即自变量x发生变换时频率分量值保持不变。

创造属于你自己的变换

傅里叶认为正余弦函数或复指数函数是构成世界的基础，创造了傅里叶变换。是否存在其他变换呢，沃尔什认为矩形方波是构成世界的基础，创造了沃尔什变换。那么如何创造属于你自己的变换呢？

1、找一组你认为构成世界的完备正交基，该正交基构成一个内积函数空间。

2、将原函数和每个基进行内积运算，得到变换系数。

3、原函数可表达为每个基乘以对应变换系数的和，即可将原函数投影到内积函数空间。

发散

假设一个多元函数s(x,y,z,...)，其自变量{x,y,z,...}随着时间t一起改变，而导致函数值s也改变，将函数记为s(t)，在确定的时间都有确定的值，如s(t0)，s(t1)，s(t2)等。当然t也可以理解为空间。

假设观测到宇宙中不知名的信号，不知道其多元函数原始表达式s(x,y,z,...)，只能通过测量得到s(t)，s(t)受限于观察者所在的时空，可能测不到某些高维时空值，只能算原始表达式s(x,y,z,...)的观察表达式。

举例说明，假设观察者所处的三维时空为内积函数空间，如果观察表达式s(t)是一个二维椭圆，那么假设原始表达式s(x,y,z,...)也一定是二维椭圆，但如果观察表达式s(t)是一个三维空间球体，可能无法证明原始表达式s(x,y,z,...)是三维还是四维甚至更高维空间球体。

量子不确定性怎么来的，为什么对于电子双缝干涉实验会有观察者效应，是不是也受限于观察者时空局限呢，也许可以在光通信与物理篇尝试探讨。

光通信与数学剩余内容

OOPING

18171226206 (WeChat)

ooping@amazelink.cn

每周不超过50%的几率随机更新，专注光通信与数学、物理、软件的交集！

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！