Needleman-Wunsch全局序列比对算法
文章目录
- 一、问题描述
- 二、设计算法
- 1. 算法策略
- 2. 数据结构
- 3. 求解步骤
- 三、实现算法
- 1. Main.java
- 2. 测试
- 四、复杂度分析
一、问题描述
尝试找到两个完整的序列 S1 和 S2 之间的最佳比对。如S1=GCCCTAGCG S2=GCGCAATG 如果设定每个匹配字符为1分,每个空格为-2分,每个不匹配为-1分,则下面的比对就是全局最优比对:S1’=GCCCTAGCG S2’=GCGC_AATG,连字符“_”代表空格。在 S2’ 中有五个匹配字符,一个空格(或者反过来说,在 S1’ 中有一个插入项),有三个不匹配字符。这样得到的分数是 (5×1) + (1×-2) + (3×-1) = 0,这是能够实现的最佳结果。
二、设计算法
1. 算法策略
Needleman-Wunsch全局序列比对算法:
它的思路与 LCS 算法相似。这个算法也使用二维表格,一个序列沿顶部展开,一个序列沿左侧展开。而且也能通过以下三个途径到达每个单元格:1.来自上面的单元格,代表将左侧的字符与空格比对。2.来自左侧的单元格,代表将上面的字符与空格比对。3.来自左上侧的单元格,代表与左侧和上面的字符比对(可能匹配也可能不匹配)。该单元格的值来自于以下3个中的最大值:(1)上方的值-2 (2)左边的值-2 (3)如果该单元格所在的行于所在的列对应的字符相等,则为左上值加1,否则为左上值-1。

2. 数据结构
① 得分矩阵
二维数组dp表示得分矩阵,s1位于dp数组的上方,s2位于dp数组的左方其中dp[i][j] 表示s1[0:j]与s2[0:i]的最高得分。
② 父节点矩阵
二维数组status记录当前节点的父节点。status[i][j] 记录dp[i][j] 的父节点。1代表左上角,2代表左边,4代表上边,若有多解也可表示,3=1+2,5=1+4,6=2+4,7=1+2+4。
3. 求解步骤
① 初始化得分矩阵
初始化第0行:所有节点的得分依次-2,且父节点均来自左边,status[0][j] = 2;
初始化第0列:所有节点的得分依次-2,且父节点均来自上边,status[i][0] = 4。
② 计算得分矩阵的每一项
状态转移方程(得分体系):dp[i][j] = max{ 1. dp[i-1][j-1] +/- 1 左上角
2. dp[i][j-1] - 2 左边s2为空
4. dp[i-1][j] - 2 上边s1为空
}
并填充status[i][j]。
③ 回溯,得到最优解
通过status数组进行回溯构造所有解,进行字符串拼接,最后反转得出所有正确解。
④ 输出打印
最优值(最高得分) = dp[n][m],打印由③所得的最优解s1和s2。
三、实现算法
1. Main.java
package com.全局序列比对;import java.util.Scanner;/*** @author fanb* @email fanb@nwafu.edu.cn* 问题描述* 尝试找到两个完整的序列 S1 和 S2 之间的最佳比对。* 如果设定每个匹配字符为1分,每个空格为-2分,每个不匹配为-1分,** 求解策略* Needleman-Wunsch(尼德曼-翁施)算法:* 它的思路与 LCS 算法相似。这个算法也使用二维表格,一个序列沿顶部展开,一个序列沿左侧展开* s1位于dp数组的上方,s2位于dp数组的左方* dp[i][j]得分矩阵 表示s1[0:j] 与 s2[0:i]的最高得分* 状态转移方程(得分体系) dp[i][j] = max{* 1. dp[i-1][j-1] +/- 1 左上角* 2. dp[i][j-1] - 2 左边s2为空* 4. dp[i-1][j] - 2 上边s1为空* }* 回溯找出最优解 status[i][j] 表示dp[i][j] 的父节点 1.左上角 2.左边 4.上边* 若有多解也可表示:3=1+2,5=1+4,6=2+4,7=1+2+4** 时间复杂度 O(m*n)* 空间复杂度 O(m*n)*/
public class Main {public static void main(String[] args) {Scanner scanner = new Scanner(System.in);System.out.print("输入s1:");String s1 = scanner.next();System.out.print("输入s2:");String s2 = scanner.next();scanner.close();Solution solution = new Solution(s1, s2);int ans = solution.needlemanWunsch(); // 求解最优值System.out.println("最优值:"+ans);solution.print(); // 打印最优解}
}class Solution{String s1,s2; // s1上侧 s2左侧int m, n; // m列 n行int[][] dp; // 得分矩阵int[][] status; // 记录父节点,1(2^0)代表左上,2(2^1)代表来自左边(左空格),4(2^2)代表来自上边(上空格)// 构造器public Solution(String s1, String s2) {this.s1 = s1;this.s2 = s2;this.m = s1.length();this.n = s2.length();this.dp = new int[n+1][m+1];this.status = new int[n+1][m+1];status[0][0] = 0;dp[0][0] = 0;}// Needleman-Wunsch 全局序列比对算法public int needlemanWunsch(){// 初始化第0列for (int i = 1; i <= n; i++) {dp[i][0] = dp[i-1][0] - 2;status[i][0] = 4;}// 初始化第0行for (int i = 1; i <= m; i++) {dp[0][i] = dp[0][i-1] - 2;status[0][i] = 2;}// 动态规划,填满dp数组for (int i = 1; i <= n; i++) { // 行for (int j = 1; j <= m; j++) { // 列int leftTop = dp[i-1][j-1] + (s1.charAt(j-1) == s2.charAt(i-1) ? 1 : -1); // 左上角int left = dp[i][j-1] - 2; // 来自左边 左空格int top = dp[i-1][j] - 2; // 来自上边 上空格int state = 0;int max = Math.max(leftTop, left); // 当前位置最高得分max = Math.max(top,max);// 左上角if(leftTop == max) state += 1;// 来自左边 左空格if(left == max) state += 2;// 来自上边 上空格if(top == max) state += 4;status[i][j] = state;dp[i][j] = max;// System.out.print(max + " ");}// System.out.println();}return dp[n][m];}// print 回溯dp二维数组输出最优解public void print(){StringBuilder s11 = new StringBuilder();StringBuilder s22 = new StringBuilder();boolean kind = false; // 标志位,判断是否有多种情况int i, j;while(true){s11.append(' ');s22.append(' ');kind = false;i = n; // 行j = m; //列while(status[i][j] != 0){switch (status[i][j]){case 1: // 只来自左上角s11.append(s1.charAt(j-1));s22.append(s2.charAt(i-1));i--;j--;break;case 2: // 只来自左空格s11.append(s1.charAt(j-1));s22.append('_');j--;break;case 3: // 来自 1 + 2// 若kind已经为true,说明已经走了一个分支,此时不需要-2if(!kind){status[i][j] -= 2;kind = true;}s11.append(s1.charAt(j-1));s22.append('_');j--;break;case 4: // 只来自上空格s11.append('_');s22.append(s2.charAt(i-1));i--;break;case 5: // 来自 1 + 4case 6: // 来自 2 + 4case 7: // 来自 1 + 2 + 4// 若kind已经为true,说明已经走了一个分支,此时不需要-4if(!kind){status[i][j] -= 4;kind = true;}s11.append('_');s22.append(s2.charAt(i-1));i--;break;}}if(!kind) break;}System.out.println("s1:" + s11.reverse());System.out.println("s2:" + s22.reverse());}
}
2. 测试
测试用例
S1=GCCCTAGCG
S2=GCGCAATG
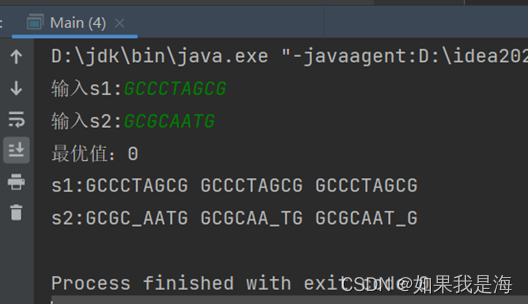
测试结果(存在多解)
最优值:0
s1: GCCCTAGCG GCCCTAGCG GCCCTAGCG
s2: GCGC_AATG GCGCAA_TG GCGCAAT_G
四、复杂度分析
(1)时间复杂度
初始化第0行T(m),初始化第0列T(n),填充得分矩阵T(mn)
T = T(mn) + T(m) + T(n)
所以时间复杂度:O(m*n)
(2)空间复杂度
得分矩阵dp[n+1][m+1]占(n+1)(m+1),父节点矩阵status[n+1][m+1]占(n+1)(m+1)
S = 2mn + 2m + 2n + 2
所以空间复杂度:O(m*n)
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!