python: 估算根号二的五种算法和实例

1.法一        夹逼法（自创）

算法来源(56条消息) 如何算根号2_根号2怎么算_光哥_帅的博客-CSDN博客 ​​​​​​

上文使用了一个比较巧妙的方法迭代逼近根号二  用y1和y2夹逼根号2

def fun(t):y1, y2 = 1, 2x = 1for i in range(t):y1 = xy2 = 2 / y1x = (y1 + y2) / 2return x
print(fun(100))

t是夹逼的次数 越大精度越高

2.法二   连分法

算法

def fun(t):last = 1 / 3#初始化时的分母 取多少都可以  在循环计算的次数多的情况下都忽略不计了for i in range(t):last = 2 + 1 / lastsum = last - 1return sum
print(fun(100))

t是循环的次数 越大精度越高

3.法三  二分法

思路：取中间值，计算中间值的平方是否等于这个值？

           1、如果等于，则返回中间值（就是结果值）；

           2、如果大于，那取下方的区间，继续求值；

           3、如果小于，那取上方的区间，继续求值。

def fun():down, up = 1, 2while up - down > 0.0000001:mid = (down + up) / 2if mid ** 2 < 2:down = midelse:up = midreturn down
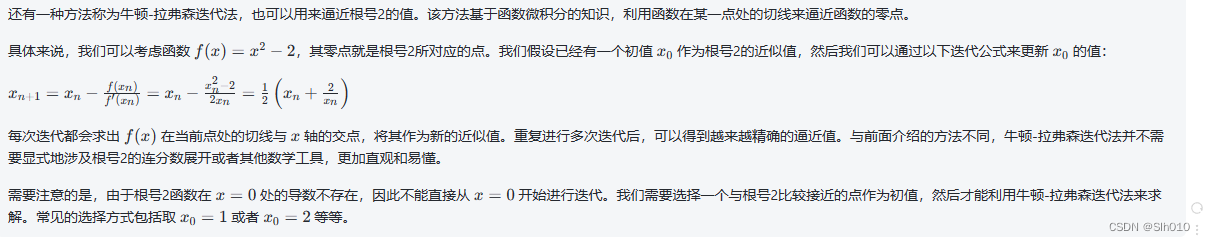
print(fun())

4.法四   牛顿迭代

 百度

def fun():x = 1while abs(x * x - 2) > 0.000001:#精度x = (x + 2 / x) / 2return x
print(fun())

5.法五     泰勒公式

#泰勒公式
def s(n): x = 1   for i in range(n):x = 0.5 * (x + 2 / x)   return x
result = s(10)
print("%.6f" % result)

注：也可以使用装饰器函数来查看计算时间  来判断算法的效率（前提是计算精度等得统一）

#泰勒公式
import time
def timer(fun):def inner():start=time.time()t=fun()end=time.time()print("运行所用时间{}".format(end-start))return treturn inner
@timer
def fun():x = 1for i in range(8888888):x = 0.5 * (x + 2 / x)return x
addd=fun()
print("根号二的近似值为{:.6f}（泰勒公式法）".format(addd))

只需要把定义fun（）函数部分改成自己的算法即可

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！