量子计算机 —— 终端应用及其限制

作者：禅与计算机程序设计艺术

文章目录

• 1.简介
• 2.背景介绍
• 3.量子计算的基本概念及术语说明
• • 3.1 量子态(Quantum State)
  • 3.2 量子门(Quantum Gate)
  • 3.3 量子比特(Quantum Bit)
  • 3.5 量子算法(Quantum Algorithm)
• 4.量子计算终端应用的技术原理及应用方向
• • 4.1 任务分解与自动调度
  • 4.2 量子加速计算
  • 4.3 可编程门阵列(Programmable Quantum Array)
  • 4.4 量子安全(Quantum Security)
  • 4.5 未来的量子计算终端应用
• 5. 量子计算基本理论和数学公式
• 6.量子计算机编程代码示例

1.简介

随着信息技术的飞速发展，越来越多的企业开始选择终端设备作为全球数字化转型的主阵地，而在终端设备上部署和运行量子计算平台则成为可能。近年来，随着量子计算机的高性能、高容错、低成本等优点逐渐受到重视，终端用户也越来越重视量子计算的应用场景。
本文以量子计算在终端应用领域的发展及其主要技术难题，提出了量子计算终端应用的五大挑战。作者通过对量子计算终端的技术研究，系统性地阐述了量子计算终端的技术原理和应用方向。同时，还指出了量子计算终端存在的技术瓶颈及其解决之道。最后，作者对未来的量子计算终端应用展望进行了展望。

2.背景介绍

量子计算（Quantum Computing）是利用物理规律之一 —— 量子力学构建的计算模型，它可以精确模拟实际世界中的很多现象，如天体物理、材料、化学反应、机器学习等。近年来，随着量子计算机的高性能、高容错、低成本等优点逐渐受到重视，终端用户也越来越重视量子计算的应用场景。根据一项调查显示，据估计全球每年产生的数据超过三万亿条，其中87%以上来自移动设备、电脑、嵌入式设备等。这就使得计算能力日益强劲的终端设备成为未来数字经济领域的重要参与者。但与此同时，由于终端设备的独特特征，使得量子计算在该领域所面临的技术难题也越来越复杂。以下将简要介绍量子计算在终端应用领域的历史、发展、技术难题以及目前正在进行的工作。

2.1 历史
量子计算机的发明最早可追溯到1982年。当时，爱丁堡大学物理学教授维纳·佩里利提出了量子引力定律，他发现它与经典的麦克斯韦方程非常不同，而这个发现被广泛认可，并得到美国国防部批准。佩里利为了证明这一点，于是发明了一台计算机。这是第一台量子计算机，也是第一个成功运行的量子计算机。

2.2 发展
由于量子计算机的潜在价值，近几十年间，数量惊人的量子计算项目陆续涌现。例如，IBM Q System One（全球量子计算中心）计划于今年8月底完成量子计算机的第一级实验测试。人工智能与机器学习领域的量子计算开源软件包ProjectQ的创始人马克·泽恩说：“量子计算已经成为第二次工业革命的征兆。”另一个量子计算领域，即在量子通信、量子信息和量子Cryptography等领域取得的突破性进展。这些突破性进展使得量子计算技术在终端领域获得更多的关注。

2.3 技术难题
在终端设备上部署量子计算平台面临的技术难题主要有以下几个方面。

首先，如何处理量子态的存储？由于量子态的大小往往是无法直接储存的，因此需要采取一定的方法对量子态进行保存和读取。目前，常用的方式包括量子纠缠、电路量子逻辑以及混合量子电路。这些方法都是有效的，但是仍然存在很大的开销。另外，由于量子态的信息熵往往较低，因此还需考虑如何压缩量子态来减少传输量。

其次，量子计算平台的资源限制。目前，终端设备的计算能力一般都比较有限，无法提供大量的量子运算。因此，如何提升计算能力就成为终端用户关心的关键问题。这就要求终端设备能够自动调度量子任务，从而更充分地发挥硬件资源。

第三，量子计算平台的安全性。当下，量子计算平台面临着严格的安全保障和法律法规。尤其是在一些敏感应用领域，诸如量子金融、量子科技、量子生物等，安全保障尤为重要。但是，如何建立起量子计算平台的安全基础、保持安全水平以及适时的更新措施，依然是一个关键问题。

第四，量子计算平台的隐私保护。虽然现代的量子计算技术可以实现任意计算，但对于某些特定应用场景来说，它可能带来隐私风险。比如，医疗影像数据对患者隐私的侵犯可能带来重大危害。如何保护个人隐私，包括数据安全、计算过程安全、控制权限分配，也是量子计算在终端领域面临的技术难题。

第五，量子计算平台的迁移和维护。随着各类终端设备的不断增长，终端用户希望他们的量子计算平台能够跨平台、跨系统迁移。而传统的方法一般仅支持单个平台或系统。因此，如何设计有效的迁移方案，减轻开发者的负担，也是量子计算终端需要解决的问题之一。

总结起来，量子计算在终端应用领域所面临的技术难题主要有三个方面：资源限制、安全性、隐私保护。解决这些技术难题的关键是优化资源利用率，增加开发者的便利性，以及完善的安全保障机制。

3.量子计算的基本概念及术语说明

3.1 量子态(Quantum State)

量子态是一个描述物质世界状态的量子系统的一组特定的波函数。它的本质是量子粒子处在空间和时间上的叠加，被称作波函数。任何给定的量子态都由两个向量构成：一维空间上的量子系综和二维空间上的量子张量积分。在这里，我们把量子态简单定义为两种形式之一——基于核素的或基于量子比特的。

基于核素的量子态表示：

如果把一个量子系统看做一个奇异微观世界，那么一个基于核素的量子态就是微观世界的一个原子。这里的核素是一个类似电子的虚构的粒子，它和其他所有原子一样，具有自己的位置和运动，并且可以按照量子态的规律运动。每个核素都有一个量子数，描述它的激发概率。

基于量子比特的量子态表示：

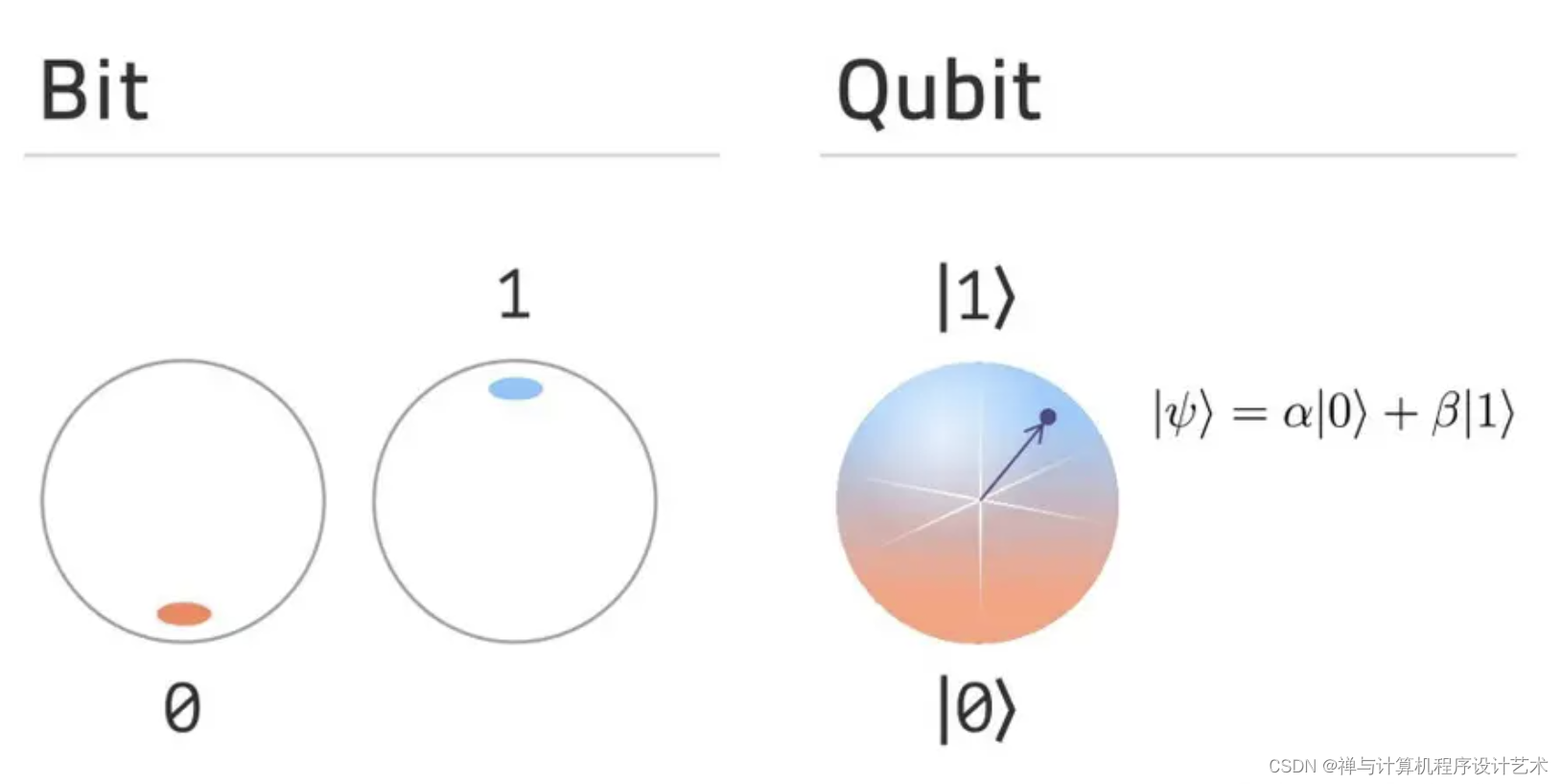
另一种表示量子态的方式是基于量子比特。这种表示方式中，每个量子比特表示一种特殊的状态，而且其叠加态代表整个系统的整体性质。量子比特可以用二进制编码来表示。具体地，每个量子比特由两个基矢表示：|0>和|1>。如果一个量子比特处于|0>状态，那么它只会受到来自另一个量子比特的量子作用。相反，如果一个量子比特处于|1>状态，它会受到量子门的所有类型的影响。

3.2 量子门(Quantum Gate)

量子门是用来转换量子态的基本操作。在实际应用中，通常将量子门分为两类——变换门和控制门。变换门是对一个量子态进行施加实用的操作，而控制门是用来控制量子门对特定量子比特的作用。

变换门：

常用的变换门有：Hadamard门、Pauli-X门、Pauli-Y门、Pauli-Z门、S门、T门、CNOT门等。它们的作用是施加特定算符对一个量子态的作用。例如，Hadamard门作用在一个量子态上会令该态变换到一个新的状态，它将一个量子比特的两个基矢分成两部分。此外，还有如Pauli-X、Y、Z门，它们都只是对不同的算符进行施加，但无论如何，都会改变量子态。

控制门：

控制门的作用是对特定量子比特施加量子门。具体地，控制门可以对零态和一个态之间进行切换，或者对一个态的一个子集施加一个门。控制门有如CNOT、SWAP、Toffoli门等。

3.3 量子比特(Quantum Bit)

量子比特是量子计算的最小单元，它是一个基本的信息处理元素。它由两级原子和离子构成，如图3-1所示。

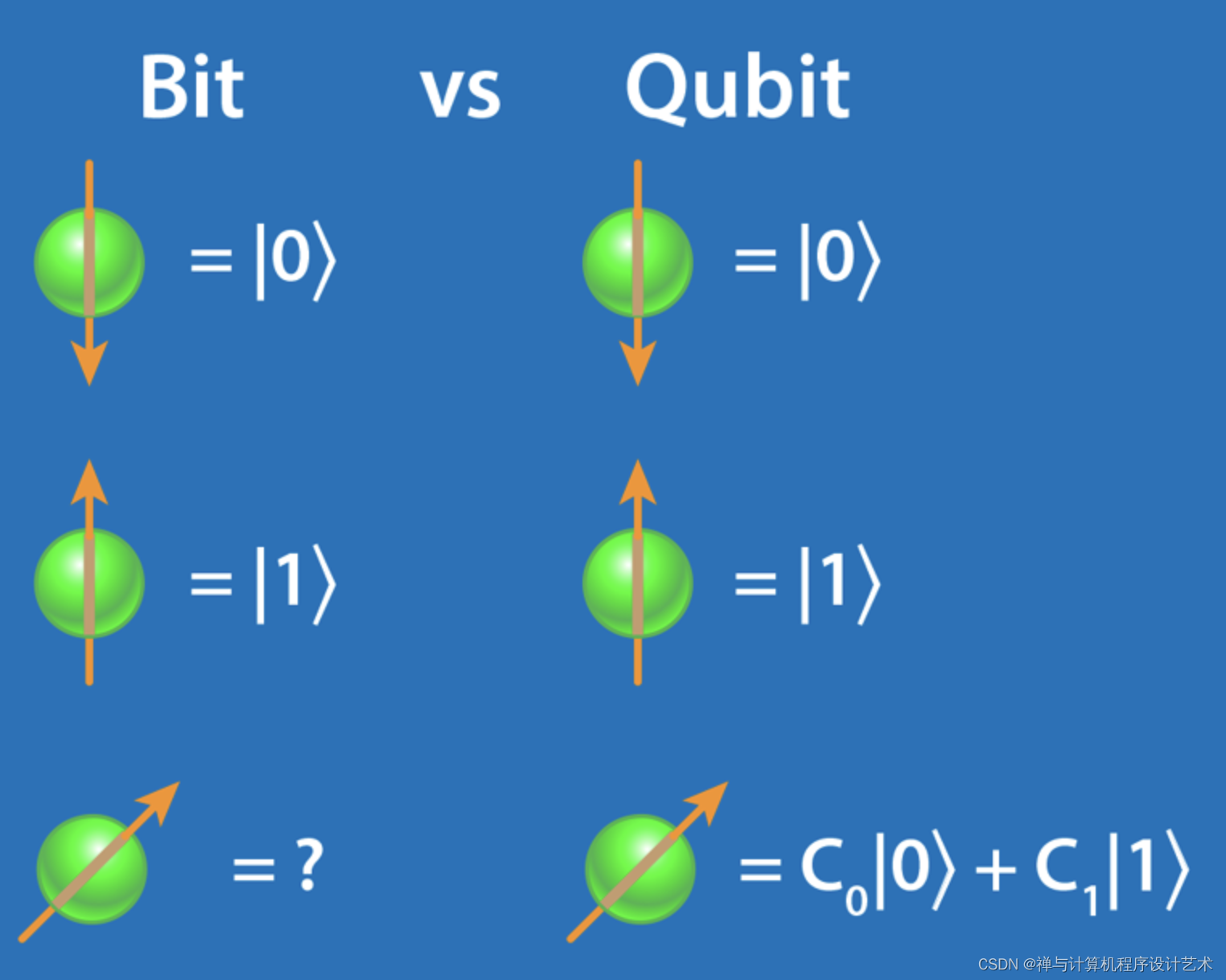
图3-1 量子比特的基本结构

从上图可以看到，每个量子比特由两个基矢组成，分别代表两个不同的量子态，它们之间的区别在于它们的能量差异。它们既可以通过外界的物理介质激发也可以被量子物理学干扰。由于量子比特的存在，才使得量子计算机的计算效率达到了前所未有的高度。

3.4 量子态的演化(Evolution of Quantum States)
量子态的演化，其实就是指量子系统从初始态到最终态的变化过程。通过演化过程，我们可以对量子系统进行各种测量，从而获得信息。在量子计算中，量子态的演化通常以矩阵的形式出现，而矩阵乘法是物理系统的基本演化规则。具体地，假设一个量子态可以写成如下形式：

∣ ψ ⟩ = ∑ i = 0 n − 1 c i ∣ i ⟩ |\psi\rangle = \sum_{i=0}^{n-1} c_i |i\rangle ∣ψ⟩=i=0∑n−1​ci​∣i⟩ （1）

这里，$|i⟩$是$n$个量子比特的基矢构成的超矢，而 c i c_i ci​是$n$个非负实数，它们的和为1。那么，如何找到另外一个与初态相同的量子态呢？通过将初态作用在某种矩阵变换上，就可以把初态变换到另一个量子态上。比如，在图3-2中，可以看到两个量子比特的基态都为$|0⟩$，通过一个CNOT门的作用，可以将两个量子比特的基态切换，变成$|0,1⟩$。

图3-2 CNOT门演化

对矩阵乘法不了解的读者可以参考线性代数相关知识。假设有两个矩阵$A$和$B$，则它们的乘积可以写成：

A B = ( a 11 a 12 a 21 a 22 ) ( b 11 b 12 b 21 b 22 ) = ( a 11 b 11 + a 12 b 21 a 11 b 12 + a 12 b 22 a 21 b 11 + a 22 b 21 a 21 b 12 + a 22 b 22 ) AB=\begin{pmatrix} a_{11} & a_{12} \\ a_{21} & a_{22}\end{pmatrix}\begin{pmatrix} b_{11} & b_{12} \\ b_{21} & b_{22}\end{pmatrix}= \begin{pmatrix} a_{11}b_{11}+a_{12}b_{21} & a_{11}b_{12}+a_{12}b_{22} \\ a_{21}b_{11}+a_{22}b_{21} & a_{21}b_{12}+a_{22}b_{22}\end{pmatrix} AB=(a11​a21​​a12​a22​​)(b11​b21​​b12​b22​​)=(a11​b11​+a12​b21​a21​b11​+a22​b21​​a11​b12​+a12​b22​a21​b12​+a22​b22​​) （2）

这里， a i j a_{ij} aij​和 b k l b_{kl} bkl​是$2\times 2$矩阵的元素，$\alpha ,\beta ,\gamma ,\delta$是实数。假设$A=(\alpha I+\beta X)$,$B=(\gamma Y+\delta Z)$，那么：

A B = α ( γ I − δ Z ) + β ( δ I + γ Z ) = ( α γ − α δ β γ β δ ) A B=\alpha(\gamma I-\delta Z)+\beta(\delta I+\gamma Z)=\begin{pmatrix} \alpha\gamma & -\alpha\delta \\ \beta\gamma & \beta\delta\end{pmatrix} AB=α(γI−δZ)+β(δI+γZ)=(αγβγ​−αδβδ​) （3）

所以，通过将初态作用在某个矩阵变换上，就可以把初态变换到另一个量子态上。而这正是量子计算的核心思想。

3.5 量子算法(Quantum Algorithm)

量子算法是指使用量子计算对某些问题求解的方法。它通常包括准备一个量子态，然后对量子态进行演化，从而找出一组数学关系。许多量子算法被认为是一种黑箱，用户无法直接理解其内部工作原理，只能通过输入输出进行交互。

4.量子计算终端应用的技术原理及应用方向

4.1 任务分解与自动调度

当下，量子计算的应用范围已扩展到各种业务领域，包括金融、生物、机器学习、遥感、物流等。因此，如何将一个复杂的任务拆分成若干个简单的子任务，以及如何自动调度这些子任务，成为当前量子计算终端的技术难题。

解决这一问题的一个关键方法是将原子任务分解成多个并行执行的小任务，然后让这些小任务自动调度到量子计算平台上。通过分解任务，可以降低任务的计算复杂度，提高其执行效率。此外，还可以通过利用资源管理器对任务进行优先级排序，这样就可以保证高优先级任务的快速执行，而低优先级任务可以排队等待执行。

除了分解任务外，还可以使用其他方法来减少任务之间的依赖性，并提高任务的并行度。譬如，可以使用分布式计算框架将同一个量子算法在不同的处理单元上并行执行。另外，也可以采用异步编程模型，以减少数据通信的开销，提高量子计算性能。

总之，自动调度可以极大地提升量子计算平台的吞吐量和利用率，同时还可以降低开发者的负担。

4.2 量子加速计算

当前，大部分的量子计算平台都是基于硬件（如量子门、量子芯片等）的量子计算。然而，随着量子算法的不断发展，越来越多的应用开始调用量子计算平台的功能，如图形处理、量子化学、量子机器学习、量子通信等。因此，如何通过改造硬件和软件的方式，提升平台的计算能力和计算密度，成为当前量子计算终端的技术难题。

一种方法是利用树状结构的量子芯片。这种芯片可以将量子门、逻辑门、噪声门等层层叠加，构成一个神经网络，从而提升量子计算能力。此外，还可以使用集成电路方式代替真空管，减少硬件的尺寸。

另一种方法是使用编译器来提升计算效率。目前，常用的编译器有Qiskit、Cirq、ProjectQ和Pyquil。它们都可以将经典的程序转换为可运行于量子计算机的指令序列。因此，通过将经典程序转换为量子程序，可以在一定程度上提升量子计算效率。

总之，量子计算终端的突破性进展主要体现在提升计算能力上。

4.3 可编程门阵列(Programmable Quantum Array)

随着量子计算的推广，许多量子算法都具有巨大的潜力，如量子密码学、量子随机性、量子电路和量子机器学习等。因此，如何搭建具有可编程性的量子计算平台成为终端用户的技术难题。

一种方法是基于云计算平台。云计算平台可以提供完整的量子计算环境，开发者可以把算法编写为可运行于云平台上的代码，再通过云平台提交到服务器上执行。这么做的好处是开发者不需要购买自己的硬件设备，减少了购买成本，同时又能享受云平台提供的高性能计算能力。此外，云平台还可以自动分配计算资源，可以满足不同量子任务的计算需求。

另一种方法是直接使用量子计算芯片。目前，量子计算芯片厂商正在探索基于可编程门阵列的量子计算平台，这种平台可以通过软件编程接口直接操控量子比特的行为。这种方法有助于降低开发者的编程难度，提高应用效率。

总之，基于可编程门阵列的量子计算终端应用已逐步成为量子计算领域的热点。

4.4 量子安全(Quantum Security)

量子安全问题一直是量子计算领域的难题。过去几十年里，世界各国政府通过各种手段，试图对量子计算技术进行攻击和破坏。但尽管近年来国家和企业开始谨慎对待量子安全问题，但其影响仍然巨大。

近期，美国国防部、英国政府以及俄罗斯联邦外交部等国际组织联合发布了一个报告，报告指出，由于量子计算技术的突破和增长，恐怕会引起政权更迭，使得国家间的政治联系更加紧密，甚至威胁到全球秩序。为了避免这种危险，技术领导者和产业界应当展开共同行动，抓住机遇，加强应对意识，确立国际合作框架，共同应对量子计算技术的挑战。

量子安全一直是一个具有挑战性的领域，只有在未来，才能看到其进一步的发展。量子计算终端的应用已经成为技术领域的重要领域，如何提升量子计算终端的安全水平也将成为技术领域的亟待解决的问题。

4.5 未来的量子计算终端应用

量子计算终端应用的未来，将不仅仅局限于量子计算领域。当前，随着物联网、5G和人工智能的发展，智能制造业也越来越蓬勃发展。智能制造业正在以惊人的速度发展，它将使量子计算技术逐渐走进制造业的每一个环节。如何将量子计算技术用于智能制造领域，打通智能制造系统中的各个环节，将成为量子计算终端应用不可替代的关键技术。

5. 量子计算基本理论和数学公式

量子计算是一种利用量子力学原理进行信息处理和计算的新兴领域。它的基本理论和数学公式涉及到量子力学、线性代数和复数等数学概念。下面是一些与量子计算相关的基本理论和数学公式：

1. 量子比特（Qubit）表示：量子比特是量子计算的基本单位，类似于经典计算中的比特（bit）。一个量子比特可以表示为一个复数的线性组合，通常用列向量表示：
   |ψ⟩ = α|0⟩ + β|1⟩
   其中，α和β是复数，|0⟩和|1⟩是基态，也称为计算基。α和β的模的平方表示量子比特处于相应基态的概率。

2. 叠加态（Superposition）：量子比特可以处于多个状态的叠加态，这是量子计算的关键特性。例如，一个量子比特可以同时处于0态和1态的叠加态：
   |ψ⟩ = α|0⟩ + β|1⟩
   其中，α和β是复数，并且满足 |α|^2 + |β|^2 = 1。

3. 测量（Measurement）：在量子计算中，测量操作用于获取量子比特的信息。测量的结果是量子比特处于某个基态的概率。测量操作会使量子比特塌缩到某个基态上，测量结果是离散的。

4. 量子门（Quantum Gate）：量子门是用于对量子比特进行操作和控制的基本单元。常见的量子门包括Hadamard门、Pauli门、CNOT门等。量子门可以表示为一个幺正矩阵，其作用是对量子比特进行线性变换。

5. 量子态的演化：量子系统的演化可以用量子力学的时间演化算符来描述。在闭合量子系统中，量子态的演化可以由薛定谔方程或者量子力学的时间演化算符来描述。

6. 量子态的纠缠（Entanglement）：纠缠是量子力学中一种特殊的关联性质，当两个或多个量子比特之间存在纠缠时，它们的状态是无法通过单个量子比特的描述来表示的。纠缠是量子计算中实现并行计算和量子通信的基础。

这些是量子计算中的一些基本理论和数学公式，量子计算的数学概念和工具还包括了更深入的量子力学、线性代数、概率论和信息论等领域的知识。

6.量子计算机编程代码示例

下面是一个简单的量子计算机编程代码示例，使用Qiskit库来进行量子程序的编写和模拟。

# 导入必要的库
from qiskit import QuantumCircuit, transpile, assemble, Aer, execute# 创建一个量子电路
qc = QuantumCircuit(2, 2)  # 2个量子比特和2个经典比特# 在量子电路中添加量子门操作
qc.h(0)  # 应用Hadamard门到第一个量子比特
qc.cx(0, 1)  # 应用CNOT门，第一个量子比特作为控制位，第二个量子比特作为目标位# 添加测量操作
qc.measure([0, 1], [0, 1])  # 将两个量子比特测量到对应的经典比特上# 编译和模拟量子电路
simulator = Aer.get_backend('qasm_simulator')  # 使用QASM模拟器
job = execute(qc, simulator, shots=1000)  # 运行1000次模拟
result = job.result()  # 获取结果# 打印模拟结果
counts = result.get_counts(qc)
print("模拟结果:", counts)

这个示例代码创建了一个包含两个量子比特和两个经典比特的量子电路。它应用了Hadamard门到第一个量子比特，然后使用CNOT门将第一个量子比特作为控制位，第二个量子比特作为目标位。最后，对两个量子比特进行测量，并将结果存储到对应的经典比特上。

然后，使用QASM模拟器对这个量子电路进行编译和模拟。通过运行1000次模拟，获取模拟结果并打印出来。

请注意，这只是一个简单的示例，用于演示量子计算机编程的基本概念。实际的量子计算机编程可能涉及更复杂的电路和算法，以及更高级的量子库和工具。

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！