清华大学学生程序设计竞赛暨高校邀请赛(THUPC)2023 - 初赛(待补题)
心得
看题跟榜比较无力,最终5h4题罚坐
M. 世界杯
输出China即可
K. 众数(前缀和)
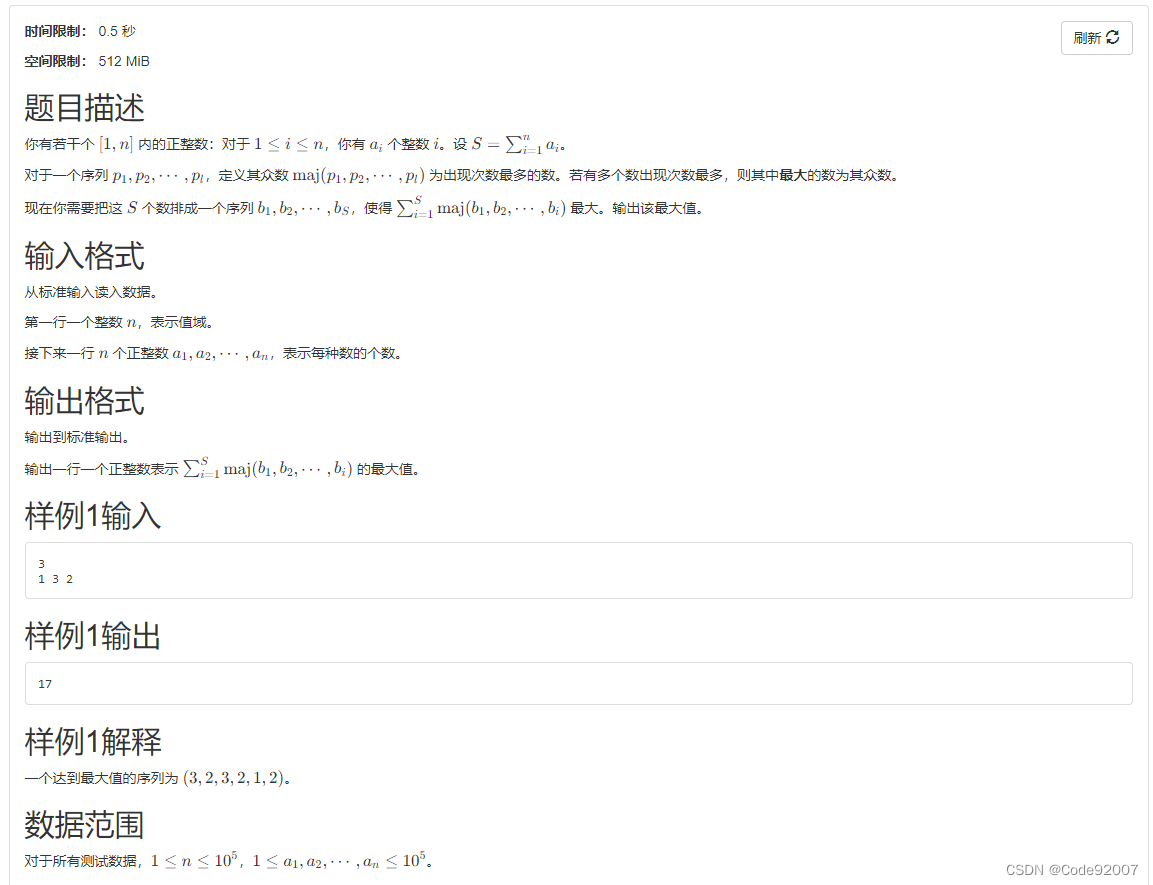
最优策略是先取最大的数x,设其出现次数为cnt[x],
然后把小于x的数y每个取min(cnt[y],cnt[x]),
下一轮再取剩下的最大的数x,重复这个过程,直至所有数都取完
由于前缀是一定要取的,后缀一定会取完,
所以,维护前缀和、前缀已经取了多少个数即可,统计每个数的贡献
#include
using namespace std;
typedef long long ll;
const int N=1e5+10;
int n,a[N],b[N],pos[N];
ll ans,now,sum[N],del;
ll cal(int x,int v){return 1ll*(n-x)*v+sum[x];
}
int main(){scanf("%d",&n);for(int i=1;i<=n;++i){scanf("%d",&a[i]);b[i]=a[i];}sort(b+1,b+n+1);for(int i=1;i<=n;++i){sum[i]=sum[i-1]+b[i];}for(int i=1;i<=n;++i){pos[i]=upper_bound(b+1,b+n+1,a[i])-b;pos[i]--;//printf("i:%d pos:%d cal:%lld\n",i,pos[i],cal(pos[i],a[i]));}for(int i=n;i>=1;--i){if(a[i]<=now)continue;now=a[i];ans+=1ll*i*(cal(pos[i],a[i])-del);//printf("now:%lld cal:%lld del:%lld add:%lld\n",now,cal(pos[i],a[i]),del,1ll*now*(cal(pos[i],a[i])-del)*a[i]);del=cal(pos[i],a[i]);//printf("i:%d now:%lld pos:%d sum:%lld add:%lld\n",i,now,pos[i],sum[pos[i]],1ll*now*pos[i]*a[i]);}printf("%lld\n",ans);return 0;
}
A.大富翁(树上博弈)

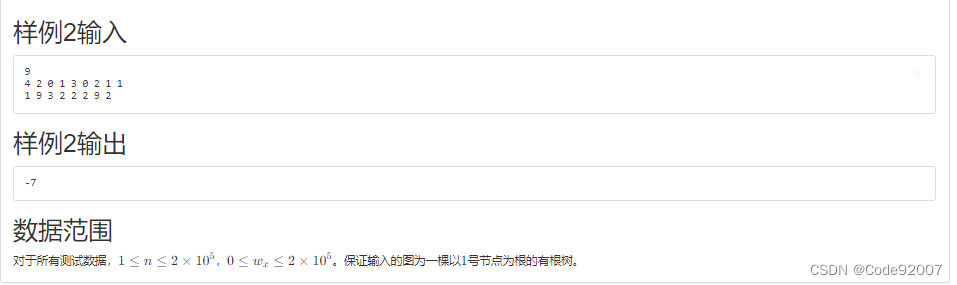
注意到,若a是b的祖先,则a支配b,
a和b被不同的人选时,选a的人+1,选b的人-1,
而若被相同的人选时,选a的人+1,选b的人-1,也恰能抵消为0
所以,每个点贡献独立,
点u赚的游戏币=子树点的个数sz[u]-它的深度d[u](即祖先点的个数)-支付游戏币的个数w[u]
而双方都是为了花的少赚得多的最优策略,
所以奇偶选取,统计先手赚取的金额即可
#include
using namespace std;
typedef long long ll;
const int N=2e5+10;
vectore[N];
int n,fa,w[N],a[N],sz[N],my,you;
ll ans;
void dfs(int u,int d){a[u]=-w[u]-d;sz[u]=1;for(auto &v:e[u]){dfs(v,d+1);sz[u]+=sz[v];}a[u]+=sz[u]-1;
}
int main(){scanf("%d",&n);for(int i=1;i<=n;++i){scanf("%d",&w[i]);}for(int i=2;i<=n;++i){scanf("%d",&fa);e[fa].push_back(i);}dfs(1,0);sort(a+1,a+n+1,greater());for(int i=1;i<=n;++i){if(i&1)ans+=a[i];}printf("%lld\n",ans);return 0;
}
I. 欺诈游戏(博弈&概率/纳什均衡)
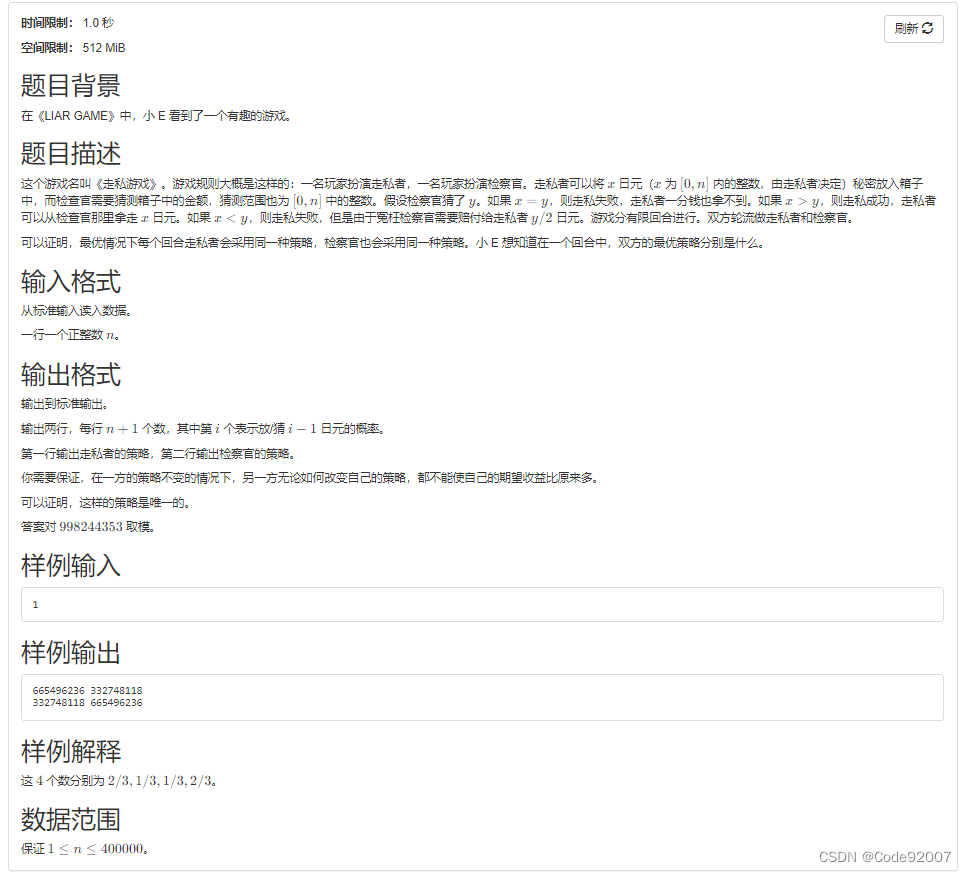
事实上,如果画一张表格,
| 走私者概率\检察官概率 | w0 | w1 |
| p0 | × | 1/2 |
| p1 | 1 | × |
以不同角色的视角,合并同类项,
把一方看做是变量时,其余所有看作是常量
对于走私者来说,收益形如,
此时,对于检察官来说,令n个系数都相同,
即走私者不管怎么选择,走私者都只能获得固定收益,
检察官达到了使对方利益最小化的目的(不存在比这大的可能性)
对于检察官来说,收益形如
此时,对于走私者来说,令n个系数都相同,
即检察官不管怎么选择,走私者都只能获得固定收益,
走私者达到了自己利益最大化的目的(不存在比这小的可能性)
#include
using namespace std;
typedef long long ll;
const int N=1e6+10,mod=998244353;
int n,p[N],w[N],sump,sumw,is,ip,inv[N];
int modpow(int x,int n,int mod){int res=1;for(;n;n>>=1,x=1ll*x*x%mod){if(n&1)res=1ll*res*x%mod;}return res;
}
void init(){inv[1]=1;for(int i=2;i
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!