自动控制原理学习笔记（三）

第三章 时域分析

文章目录

• • 第三章 时域分析
  • • 3.1 典型输入信号
    • ==3.2 线性系统时域性能指标（稳定系统）==
    • 3.3 一阶系统
    • • ①单位阶跃响应
      • ②单位脉冲响应
      • ③单位斜坡响应
      • ④单位匀加速度响应
    • 3.4线性定常系统重要特性
    • 3.5 二阶系统
    • • 3.5.1 二阶系统单位阶跃响应
      • • ①★欠阻尼★
        • ②无阻尼
        • ③临界阻尼
        • ④过阻尼
        • ⑤负阻尼
        • 二阶系统动态性能随极点位置分布的变化规律
      • 3.5.2 二阶系统单位脉冲响应
      • • 无阻尼
        • 欠阻尼
        • 临界阻尼
      • 3.5.3 二阶系统单位斜坡响应
    • 3.6 高阶系统
    • • 一些结论
      • 主导极点
    • 3.7基于脉冲传递函数的离散系统时域分析 (6.8.1~6.8.2)
    • • 极点分布与响应
    • 3.8 基于状态空间的时域分析
    • • 线性定常连续系统
      • • 运动分析
        • 状态转移矩阵
        • 齐次方程求解（零输入）
        • ==非齐次方程求解==
      • 离散系统
      • • ==线性定常连续系统状态方程的离散化==
        • 线性定常离散系统状态方程的解

• 特点：

  • 分析设计直观准确
  • 提供时间响应的全部信息
  • 解析解较繁琐

• 方法步骤

  1. 传递函数
  2. 通过逆变换求出时域响应$y(t)$
  3. 根据$y(t)$分析系统性能

3.1 典型输入信号

1. 单位脉冲
2. 单位阶跃
3. 单位匀速
4. 单位加速度
5. 正弦

3.2 线性系统时域性能指标（稳定系统）

• 延迟时间 t d t_d td​：阶跃响应第一次到达稳态值的50%所需时间
• 上升时间 t r t_r tr​ ：稳态值10%到90%所用的时间。振荡：0到第一次稳态值所用时间
• 峰值时间 t p t_p tp​：超越终值达到第一个峰值所需时间
• 超调量 σ p \sigma_p σp​：百分比 σ p = y ( t p ) − y ( ∞ ) y ( ∞ ) × 100 % \sigma_p=\dfrac{y(t_p)-y(\infty)}{y(\infty)}\times 100\% σp​=y(∞)y(tp​)−y(∞)​×100%
• 调节时间 t s t_s ts​：到达并保持在终值5%或2%误差带内所需的最短时间
• 振荡次数 $N$：调节时间内，单位阶跃响应穿越稳态值次数的一半

3.3 一阶系统

• Φ ( s ) = 1 T s + 1 \varPhi(s) = \dfrac{1}{Ts+1} Φ(s)=Ts+11​

①单位阶跃响应

• 响应： y ( t ) = 1 − e − t T y(t)=1-e^{-\frac{t}{T}} y(t)=1−e−Tt​
• $y(T)=0.632$
• $y(3T)\approx 0.95$，即 t s = 3 T t_s=3T ts​=3T
• 无稳态误差
• 提高快速性：减小时间常数 $T$
• 由阶跃响应求 T ： d y d t ∣ t = 0 = 1 T T： \frac{dy}{dt}|_{t=0}=\frac{1}{T} T：dtdy​∣t=0​=T1​

②单位脉冲响应

• 响应： y ( t ) = 1 T e − t T , t ≥ 0 y(t)=\dfrac{1}{T}e^{-\frac{t}{T}}\ ,t\geq 0 y(t)=T1​e−Tt​ ,t≥0
• y ( 0 ) = 1 T y(0)=\dfrac{1}{T} y(0)=T1​
• y ( T ) = 0.368 1 T y(T)=0.368\dfrac{1}{T} y(T)=0.368T1​

③单位斜坡响应

• y ( t ) = t − T ( 1 − e − t T ) , t ≥ 0 y(t)=t-T(1-e^{-\frac{t}{T}})\ ,\ t\geq 0 y(t)=t−T(1−e−Tt​) , t≥0
• 稳态误差$e=T$ （减小T可以减小稳态误差）

④单位匀加速度响应

• y ( t ) = 1 2 t 2 − T t + T 2 ( 1 − e − t T ) , t ≥ 0 y(t)=\dfrac{1}{2}t^2-Tt+T^2(1-e^{-\frac{t}{T}})\ ,t\geq 0 y(t)=21​t2−Tt+T2(1−e−Tt​) ,t≥0

3.4线性定常系统重要特性

• 系统对输入信号导数的响应=系统对原信号的响应的导数
• 积分同理，积分常数由零输出时的初始条件决定

3.5 二阶系统

• $\varPhi(s) = \dfrac{Y(s)}{R(s)} = \dfrac{\omega_n^2}{s2+2\zeta\omega_n s+\omega_n^2} $
• 闭环极点： s 1 , 2 = − ζ ω n ± ω n ζ 2 − 1 s_{1,2}=-\zeta\omega_n \pm \omega_n\sqrt{\zeta^2-1} s1,2​=−ζωn​±ωn​ζ2−1 ​
• 开环传函： G ( s ) = ω n 2 s ( s + 2 ζ ω n ) G(s) = \dfrac{\omega_n^2}{s(s+2\zeta\omega_n)} G(s)=s(s+2ζωn​)ωn2​​

3.5.1 二阶系统单位阶跃响应

①★欠阻尼★

• $0<\zeta <1$
• s 1 , 2 = − ζ ω n ± j ω n 1 − ζ 2 s_{1,2}=-\zeta\omega_n \pm \mathrm j \omega_n\sqrt{1-\zeta^2} s1,2​=−ζωn​±jωn​1−ζ2 ​
• 设有阻尼振荡频率 ω d = ω n 1 − ζ 2 \omega_d = \omega_n\sqrt{1-\zeta^2} ωd​=ωn​1−ζ2 ​
• 输入单位阶跃信号，可得输出：

Y ( s ) = Φ ( s ) 1 s = 1 s − s + ζ ω n ( s + ζ ω n ) 2 + ω d 2 − ζ ω n ( s + ζ ω n ) 2 + ω d 2 \begin{aligned} Y(s) &= \varPhi(s)\dfrac{1}{s} \\ &= \dfrac{1}{s} - \dfrac{s+\zeta\omega_n}{(s+\zeta\omega_n)^2+\omega_d^2} - \dfrac{\zeta\omega_n}{(s+\zeta\omega_n)^2+\omega_d^2} \\ \end{aligned} Y(s)​=Φ(s)s1​=s1​−(s+ζωn​)2+ωd2​s+ζωn​​−(s+ζωn​)2+ωd2​ζωn​​​

• 利用Laplace变换的位移性质，可得

y ( t ) = 1 − e − ζ ω n t ( cos ⁡ ω d t + ζ ω n ω d sin ⁡ ω d t ) = 1 − e − ζ ω n t 1 1 − ζ 2 sin ⁡ ( ω d t + θ ) , t ≥ 0 \begin{aligned} y(t) &= 1-e^{-\zeta\omega_n t}(\cos \omega_d t + \frac{\zeta\omega_n}{\omega_d}\sin\omega_d t) \\ &= 1-e^{-\zeta\omega_n t}\dfrac{1}{\sqrt{1-\zeta^2}}\sin(\omega_d t+\theta) , t\geq 0\\ \end{aligned} y(t)​=1−e−ζωn​t(cosωd​t+ωd​ζωn​​sinωd​t)=1−e−ζωn​t1−ζ2 ​1​sin(ωd​t+θ),t≥0​

其 中 θ = arctan ⁡ 1 − ζ 2 ζ 或 ζ = cos ⁡ θ 其中 \theta = \arctan \dfrac{\sqrt{1-\zeta^2}}{\zeta}\ 或\ \zeta = \cos\theta\\ 其中θ=arctanζ1−ζ2 ​​ 或 ζ=cosθ

• 稳态分量、暂态分量
• 包络线: y ( t ) = 1 ± e − ζ ω n t 1 − ζ 2 y(t)=1 \pm \dfrac{e^{-\zeta\omega_n t}}{\sqrt{1-\zeta^2}} y(t)=1±1−ζ2 ​e−ζωn​t​
• 上升时间 t r = π − θ ω n 1 − ζ 2 t_r=\dfrac{\pi-\theta}{\omega_n\sqrt{1-\zeta^2}} tr​=ωn​1−ζ2 ​π−θ​, 系统快速性与 ω n \omega_n ωn​成正比
• 峰值时间 t p = π ω n 1 − ζ 2 t_p=\dfrac{\pi}{\omega_n\sqrt{1-\zeta^2}} tp​=ωn​1−ζ2 ​π​
• 超调量 σ p = e − ζ π 1 − ζ 2 × 100 % = e − π cot ⁡ θ \sigma_p=e^{-\dfrac{\zeta\pi}{\sqrt{1-\zeta^2}}}\times100\%=e^{-\pi \cot\theta} σp​=e−1−ζ2 ​ζπ​×100%=e−πcotθ
• 调节时间$t_s = \begin{cases}\dfrac{4}{\xi\omega_n}&,\Delta=0.02\ \dfrac{3}{\xi\omega_n}&,\Delta=0.05\end{cases} $
• 振荡次数 N = { 2 1 − ζ 2 π ζ Δ = 0.2 1.5 1 − ζ 2 π ζ Δ = 0.05 N = \begin{cases}\dfrac{2\sqrt{1-\zeta^2}}{\pi\zeta}&&\Delta = 0.2\\\dfrac{1.5\sqrt{1-\zeta^2}}{\pi\zeta}&&\Delta = 0.05 \end{cases} N=⎩⎪⎪⎨⎪⎪⎧​πζ21−ζ2 ​​πζ1.51−ζ2 ​​​​Δ=0.2Δ=0.05​

②无阻尼

• $\zeta =0$
• y ( t ) = 1 − cos ⁡ ω n t , t ≥ 0 y(t) = 1-\cos\omega_n t\ ,\ t\geq 0 y(t)=1−cosωn​t , t≥0
• 等幅振荡，调节时间正无穷

③临界阻尼

• $\zeta =1$
• y ( t ) = 1 − e − ω n t ( 1 + ω n t ) , t ≥ 0 y(t) = 1-e^{-\omega_n t}(1+\omega_n t)\ ,\ t\geq 0 y(t)=1−e−ωn​t(1+ωn​t) , t≥0
• y ′ ( 0 ) = 0 y^\prime(0) = 0 y′(0)=0
• 稳态为$y=1$，无超调，单调上升

④过阻尼

• $\zeta >1$

  无超调

⑤负阻尼

• $-1<\zeta <0$
• 系统不稳定，发散

二阶系统动态性能随极点位置分布的变化规律

• 左半平面
• 远离虚轴

3.5.2 二阶系统单位脉冲响应

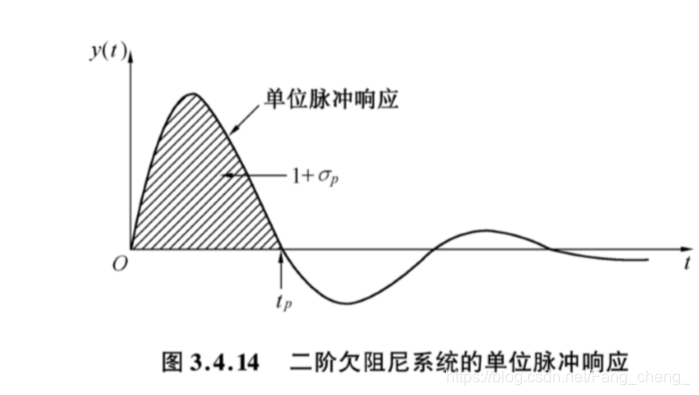
• y ( t p ) = ∫ 0 t p k ( t ) d t = 1 + σ p y(t_p) = \int_0^{t_p}k(t)\mathrm dt=1+\sigma_p y(tp​)=∫0tp​​k(t)dt=1+σp​

无阻尼

• k ( t ) = ω n sin ⁡ ω n t , t ≥ 0 k(t)=\omega_n\sin\omega_nt\ \ ,t\geq0 k(t)=ωn​sinωn​t  ,t≥0

欠阻尼

临界阻尼

3.5.3 二阶系统单位斜坡响应

3.6 高阶系统

Φ ( s ) = k ∏ j = 1 m ( s − z j ) ∏ i = 1 q ( s − s i ) ∏ k = 1 r ( s 2 + 2 ζ k ω n k s + ω n k 2 ) q + 2 r = n \varPhi(s) = \frac{k\prod\limits_{j=1}^m (s-z_j)}{\prod\limits_{i=1}^q(s-s_i)\prod\limits_{k=1}^r (s^2+2\zeta_k\omega_{nk}s+\omega_{nk}^2)}\\ \\ \\ q+2r=n Φ(s)=i=1∏q​(s−si​)k=1∏r​(s2+2ζk​ωnk​s+ωnk2​)kj=1∏m​(s−zj​)​q+2r=n

一些结论

• 若闭环极点均在左半平面，则暂态分量都将收敛到零
• 收敛速度取决于：左半平面极点距离虚轴越远越快
  1. 实极点绝对值 ∣ s i ∣ |s_i| ∣si​∣
  2. 复极点实部绝对值 ∣ ζ k ω n k ∣ |\zeta_k\omega_{nk}| ∣ζk​ωnk​∣
• 暂态分量与零点相关：
  • 若某极点靠近一零点且与其他极点相距较远，则该暂态分量影响较小
  • 若一对闭环零、极点非常接近，称作一对“偶极子”，该极点对暂态过程几乎没有影响

主导极点

若

• 一对共轭极点（或一个实极点）距虚轴最近
• 且其他极点到虚轴距离均为其5倍以上
• 虚轴附近无单独闭环零点

则该极点成为高阶系统的主导极点

3.7基于脉冲传递函数的离散系统时域分析 (6.8.1~6.8.2)

• 输入 r ( t ) = 1 , R ( z ) = z z − 1 r(t)=1,\ R(z)=\dfrac{z}{z-1} r(t)=1, R(z)=z−1z​
• 输出 y ( k T ) = A + ∑ i = 1 n B i p i k y(kT)=A+\sum\limits_{i=1}^nB_ip_i^k y(kT)=A+i=1∑n​Bi​pik​
• 瞬态响应分量： ∑ i = 1 n B i p i k \sum\limits_{i=1}^nB_ip_i^k i=1∑n​Bi​pik​

极点分布与响应

• 单位圆，详见离散系统稳定性一节

3.8 基于状态空间的时域分析

线性定常连续系统

运动分析

1. 自由运动——零输入响应

• $u=0$

2. 强迫运动——零状态响应

• x ( t 0 ) = 0 x(t_0) = 0 x(t0​)=0

状态转移矩阵

定义：对于齐次状态方程，若有 $x(t)=\Phi (t)x(0)$, 则称 $\Phi (\mathbf{t})$ 为系统的状态转移矩阵。

• 若初始时刻不为0，而是 t 0 t_0 t0​，则状态转移矩阵 Φ ( t , t 0 ) \varPhi(t, t_0) Φ(t,t0​)

• 对于线性定常连续系统，本质上仍是矩阵指数函数 e A t e^{\boldsymbol At} eAt。

• 性质：

  1. 非奇异： ( e A t ) − 1 = e A ( − t ) (e^{\boldsymbol At})^{-1}=e^{\boldsymbol A(-t)} (eAt)−1=eA(−t)

  2. 当$AB=BA$ 时， e ( A + B ) t = e A t e B t e^{(A+B)t} = e^{At}e^{Bt} e(A+B)t=eAteBt ;

     若$AB\ne BA$，则 e ( A + B ) t ≠ e A t e B t e^{(A+B)t} \neq e^{At}e^{Bt} e(A+B)t​=eAteBt

  3. 微分性质： d d t e A t = A e A t = e A t A \dfrac{\mathrm d}{\mathrm dt}e^{\boldsymbol At} = \boldsymbol Ae^{\boldsymbol At} = e^{\boldsymbol At}\boldsymbol A dtd​eAt=AeAt=eAtA （可用于：由 e A t e^{\boldsymbol At} eAt 求$\mathbf{A}$）

  4. 相似变换：

     若P为非奇异阵，即必存在 P − 1 P^{-1} P−1 ，则

     • e P − 1 A P t = P − 1 e A t P e^{P^{-1}APt}=P^{-1}e^{At}P eP−1APt=P−1eAtP

  5. 对角阵情形：

  

  6. Jordan 块

     

  7. 当A是约当矩阵时：

     

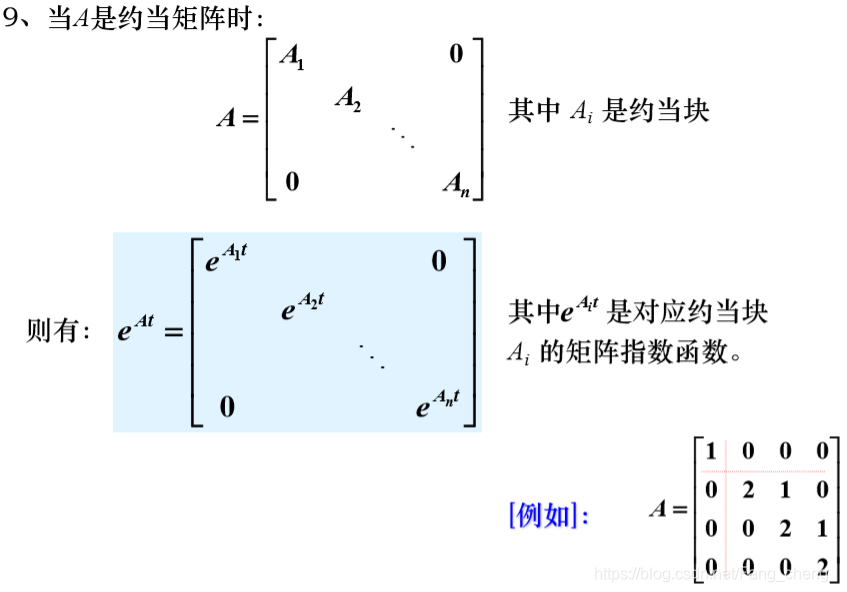
齐次方程求解（零输入）

• x ˙ = A x \dot x = \boldsymbol A x x˙=Ax ,$A$ 为nxn阶定常方阵

  • 指数函数的推广： x = e A t x 0 x = e^{\boldsymbol At}x_0 x=eAtx0​ , e A t e^{\boldsymbol At} eAt 称为矩阵指数函数

  • 矩阵指数函数定义：

    e A t = d e f = ∑ k = 0 ∞ 1 k ! A k t k = I + A t + 1 2 A 2 t 2 + ⋯ + 1 k ! A k t k e^{\boldsymbol At} =^{def}= \sum\limits_{k=0}^\infty\dfrac{1}{k!}\boldsymbol A^kt^k=I+\boldsymbol At+\dfrac{1}{2}\boldsymbol A^2t^2+\cdots+\dfrac{1}{k!}\boldsymbol A^kt^k eAt=def=k=0∑∞​k!1​Aktk=I+At+21​A2t2+⋯+k!1​Aktk

求取 **矩阵指数函数（状态转移矩阵）**的方法：

1. 定义法（级数）

   e A t = ∑ k = 0 ∞ 1 k ! A k t k = I + A t + 1 2 A 2 t 2 + ⋯ + 1 k ! A k t k e^{\boldsymbol At}= \sum\limits_{k=0}^\infty\dfrac{1}{k!}\boldsymbol A^kt^k=I+\boldsymbol At+\dfrac{1}{2}\boldsymbol A^2t^2+\cdots+\dfrac{1}{k!}\boldsymbol A^kt^k eAt=k=0∑∞​k!1​Aktk=I+At+21​A2t2+⋯+k!1​Aktk

2. Laplace变换法

• Laplace变换： $sX(s)-x(0)=\mathbf{A}X(s)$

• X ( s ) = ( s I − A ) − 1 x ( 0 ) X(s) = (s\boldsymbol I -\boldsymbol A)^{-1}x(0) X(s)=(sI−A)−1x(0)

  e A t = L − 1 [ ( s I − A ) − 1 ] e^{At}=\mathscr L^{-1} [(s\boldsymbol I -\boldsymbol A)^{-1}] eAt=L−1[(sI−A)−1]

  x ( t ) = L − 1 [ ( s I − A ) − 1 ] x ( 0 ) x(t) = \mathscr L^{-1} [(s\boldsymbol I -\boldsymbol A)^{-1}]x(0) x(t)=L−1[(sI−A)−1]x(0)

3. 凯莱哈密顿
4. 构造Jordan块

非齐次方程求解

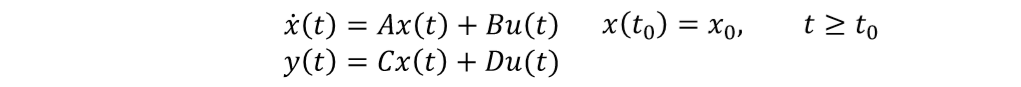
1. 积分法
   x ( t ) = e A ( t − t 0 ) x ( t 0 ) + ∫ t 0 t e A ( t − τ ) B u ( τ ) d τ x(t) = e^{A(t-t_0)}x(t_0)+\int_{t_0}^t e^{A(t-\tau)}Bu(\tau)\ \mathrm d\tau x(t)=eA(t−t0​)x(t0​)+∫t0​t​eA(t−τ)Bu(τ) dτ

2. Laplace 变换法（背下来）

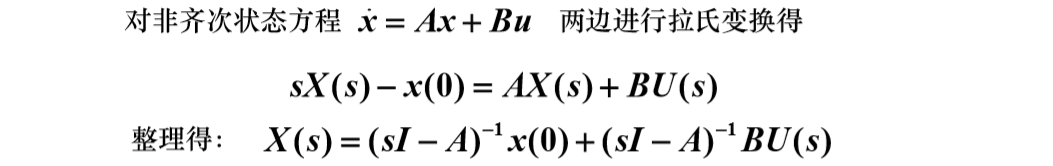
x ( t ) = L − 1 [ ( s I − A ) − 1 x ( t 0 ) + ( s I − A ) − 1 B U ( s ) ] x(t) = \mathscr L^{-1}[(sI-A)^{-1}x(t_0)+(sI-A)^{-1}BU(s)] x(t)=L−1[(sI−A)−1x(t0​)+(sI−A)−1BU(s)]

离散系统

• { x ( k + 1 ) = G x ( k ) + H u ( k ) y ( k ) = C x ( k ) + D u ( k ) \begin{cases} \boldsymbol{x}(k+1) &=& \boldsymbol{Gx}(k)+\boldsymbol{Hu}(k)\\ \boldsymbol{y}(k)&=& \boldsymbol{Cx}(k)+\boldsymbol{Du}(k) \end{cases} {x(k+1)y(k)​==​Gx(k)+Hu(k)Cx(k)+Du(k)​

线性定常连续系统状态方程的离散化

G = e A T H = ( ∫ 0 T e A t d t ) B \boldsymbol G = e^{\boldsymbol AT}\\ \boldsymbol H = (\int_0^Te^{\boldsymbol At}\ \mathrm dt)\boldsymbol B G=eATH=(∫0T​eAt dt)B

线性定常离散系统状态方程的解

1. 迭代法

x ( k ) = G k x ( 0 ) + ∑ i = 0 k − 1 G k − i − 1 H u ( i ) \boldsymbol x(k) = \boldsymbol G^k \boldsymbol x(0)+\sum_{i=0}^{k-1} \boldsymbol G^{k-i-1}\boldsymbol{Hu}(i) x(k)=Gkx(0)+i=0∑k−1​Gk−i−1Hu(i)

2. Z变换法

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！