概率 + 统计随机变量及其分布（二）

2023-12-08 04:02:46

随机变量

设随机试验的样本空间为S={e}. X=X(e)是定义在样本空间S上的实值单值函数. 称X=X(e)为随机变量.

离散型随机变量的概率分布

随机变量X的所有可能取值是有限多个或可列无限多个, 这种随机变量称为离散型随机变量。

设X所有可能取的值为 $x_k(k=1,2,...)$ , 称

$P\{X=x_k\}=p_k, k=1,2,....$ (1)

为离散型随机变量X的分布律。由概率的定义, $p_k$ 满足如下两个条件

$p_k \geqslant 0, k=1,2,\cdots$
$\sum_{k=1}^{\infty }p_k=1, k=1,2,\cdots$

分布律也可用表格的形式来表示:

三个重要的离散型随机变量

(0-1)分布

设随机变量X只可能取0与1两个值, 它的分布律是

$P(X=k)=p^k(1-p)^{1-k}, k= 0,1, \ \ (0 < p < 1)$

则称X服从以p为参数的(0-1)分布或两点分布. (0-1)分布的分布律也可写成

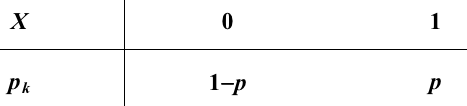
二项分布

用X表示n重贝努利试验中事件A发生的次数，则

$P(X=k)=C_n^kp^k(1-p)^{n-k},\ \ k =0,1,2,\cdots,n$

称随机变量X 服从参数为n和p的二项分布，记作X~B(n,p)

当n=1时，二项分布就是(0-1)分布。

泊松分布

设随机变量X所有可能取的值为0 , 1 , 2 , … , 且概率分布为：

$P(X=k)=\frac{\lambda^{k}}{k!}e^{-\lambda}, \ \ k=0,1,2,\cdots$

其中 $\lambda > 0$ 是常数,则称 X 服从参数为 $\lambda$ 的泊松分布,记作 $X \sim \pi(\lambda)$

泊松（Poisson）定理：设 $\lambda > 0$ 是一常数,n是任意正整数,设 $np_n=\lambda$ 则对于任一固定的非负整数k,有

$\lim_{n\rightarrow \infty}C_n^kp_n^k(1-p_n)^{n-k}=\frac{\lambda^ke^{-\lambda}}{k!}$

定理表明： n比较大, p很小时, 以n , p为参数的二项分布的概率值可以由参数为l=np的泊松分布的概率值近似。

随机变量的分布函数

设X是一个随机变量，称 $F(x)=P(X \leqslant x)(-\infty < x < +\infty)$ 为X的分布函数，记作F(X)。

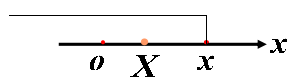
如果将 X 看作数轴上随机点的坐标，那么分布函数 F(x) 的值就表示 X落在区间 $(-\infty, x]$ 内的概率。

对任意实数 $x_1<x_2$ ，随机点落在区间 $(x_1, x_2]$ 内的概率为： $P(x_1 < X \leqslant x_2) = P(X \leqslant x_2) - P(X \leqslant x_1) = F(x_2) - F(x_1)$

连续型随机变量及其分布

对于随机变量 X , 如果存在非负可积函数 $f (x)$ , $x \in (-\infty,+\infty)$ ，使得对任意实数 $x$ ，有 $F(x)=\int_{-\infty}^{x}f(t)dt = P(X\leqslant x)$ 则称 X为连续型随机变量, 称 $f (x)$ 为 X 的概率密度函数，简称为概率密度。

对任意实数 $x_1<x_2$ ，有 $P(x_1 < X \leqslant x_2) = \int_{x_1}^{x_2}f(x)dx$

对连续型随机变量X , 有 $P(a\leqslant X \leqslant b) = P(a < X \leqslant b)=P(a\leqslant X< b)=P(a < X <b)$

三种重要的连续型随机变量

均匀分布

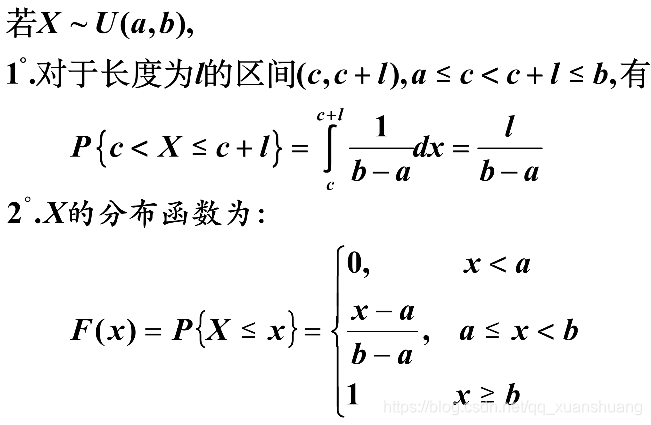
指数分布

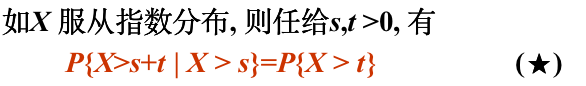
性质(★)称为无记忆性. 指数分布在可靠性理论和排队论中有广泛的运用.

正态分布

标准正态分布

正态分布与标准正态分布的分布函数之间的关系

若 $X \sim N(\mu, \sigma^2)$ ，则 $Z=\frac{X-\mu}{\sigma} \sim N(0,1)$

$X \sim N(\mu, \sigma^2) \\ \Rightarrow F_X(x)=P(X\leqslant x)=P(\frac{X-\mu}{\sigma} \leqslant \frac{x-\mu}{\sigma} ) =\varnothing (\frac{x-\mu}{\sigma})$

$P(a < X < b) = \varnothing(\frac{b - \mu}{\sigma}) - \varnothing(\frac{a- \mu}{\sigma})$

$\begin{aligned} &P(|X - \mu| \leqslant \sigma) = \varnothing(1)- \varnothing(-1)=0.6826\\ &P(|X - \mu| \leqslant 2\sigma) = \varnothing(2)- \varnothing(-2)=0.9544 \\ &P(|X - \mu| \leqslant 3\sigma) = \varnothing(3)- \varnothing(-3)=0.9974 \end{aligned}$

可以认为，X 的取值几乎全部集中在 $[\mu - 3\sigma, \mu +3\sigma]$ 区间内。这在统计学上称作" $3\sigma$ 准则"

标准正态分布的上 $\alpha$ 分位

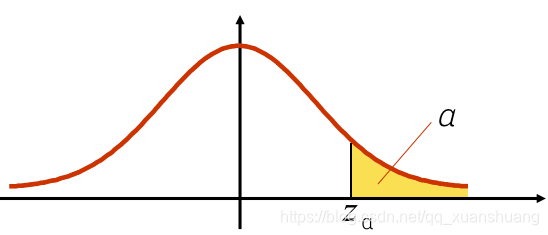
设 $X \sim N(0,1)$ ，若 $z_\alpha$ 满足条件 $P(X >z_\alpha)=\alpha, 0 < \alpha < 1$ ，则称点 $z_\alpha$ 为标准正态分布的上 $\alpha$ 分位。

由 $\varnothing(x)$ 的对称性知 $z_{1-\alpha}=-z_{\alpha}$ 。

一维随机变量函数的分布

设随机变量 X 的分布已知，Y=g (X) (设g 是连续函数），我们利用 X 的分布来求 Y 的分布。

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！

标签：技术

上一篇 > Lecture3.随机变量及其概率分布
下一篇 > 概论_第2章_重点_一个随机变量函数的概率分布___定理法和分布函数法的应用

Duilib中list控件支持ctrl和shif多行选中的实现

[ICML2015]Batch Normalization:Accelerating Deep Network Training by Reducing Internal Covariate Shif

win10系统微软输入法于eclipse ctrl+shif+f冲突间接处理办法

Codeforces Round #259 (Div. 2) B. Little Pony and Sort by Shif

读LDD3，内存映射与DMA--PAGE_SHIF…

VMware虚拟机安装XP【要先分区，再设置BOOT 启动CD，shif+上移】

更换iBus五笔的左与右Shif

sublime ctrl+shif+f 没用解决办法

idea 对 ctrl + z 的撤销是 ctrl + shif + z

计算机最早的设计师应用于,计算机应用基础选择题doc.doc

win10自带截图神器：Win+Shift+S

Python基础之文件目录操作

python简述目录_Python基础之文件目录操作(示例代码)

tp5 如何做数据采集

任务2-7(服务器字体+阿里巴巴矢量库)

html标签（1)：h1~h6,p,br,pre,hr

TI 电量计介绍与芯片选型指南

几款TI电源芯片简介

TI DSP芯片C2000系列读取FLASH数据

德州仪器(Ti)平台嵌入式开发基础

TI三相电机智能栅极驱动芯片特点分类

省选模拟（12.08） T3 圈圈圈圈圈圈圈圈

Hadoop生态圈技术栈（上）

大数据开发基础入门与项目实战（三）Hadoop核心及生态圈技术栈之6.Impala交互式查询

小猿圈之Linux下Mysql 操作命令

大数据Hadoop生态圈常用面试题

大数据开发基础入门与项目实战（三）Hadoop核心及生态圈技术栈之4.Hive DDL、DQL和数据操作

备战Noip2018模拟赛11（B组）T3 Monogatari 物语

【智能优化算法-圆圈搜索算法】基于圆圈搜索算法Circle Search Algorithm求解单目标优化问题附matlab代码

NYOJ 78 圈水池

递归问题跑道汽车绕圈问题 Python实现

Hadoop生态圈（三）：MapReduce

概率 + 统计 随机变量及其分布（二）