大数据排序(10亿量级以上)C语言实现
大数据排序(10亿量级以上)C语言实现
我们平常对数据进行排序一般用内部方法,即八大排序方法:
- 直接插入排序
- 冒泡排序
- 希尔排序
- 堆排序
- 归并排序
- 堆排序
- 快速排序
- 基数排序
这些排序方法默认你们已经掌握了,如果不了解可以在网上搜一下
首先给出设计的大纲,一共分三步:
- 先生成10亿随机数数据
- 将10亿数据分成n个小文件并进行排序
- 最后将n个小文件进行归并
这里可能大家就会有疑问了,为什么要分好几个小文件呢?
这是由于我们的堆栈无法一次性地存入10亿个数据,因此我们要进行外部排序,即分成n个小文件,然后在进行归并合到目标文件中,这样达到排序目的
主函数代码如下:
#include 接下来我们要生成随机数,我才用的是scrand函数将当前时间作为种子来随机生成无符号整型数,代码如下(random.h):
#pragma once
#include接下来就到我们的重点了,如何将数据分成n个小文件进行排序,这里我采用的是快速排序,将数据分成500个有序的数据文件这个就不赘述了很简单理解,代码如下(divid.h):
#pragma once
#include下面是我自己写的快速排序模板,如果你想用库函数也行。
#pragma once
template <class T>
int Partition(T L[], int low, int high)//一次快排
{int pivotkey;L[0] = L[low];pivotkey = L[low];while (low < high){while (low < high && L[high] >= pivotkey){--high;}L[low] = L[high];while (low < high && L[low] <= pivotkey){++low;}L[high] = L[low];}L[low] = L[0];return low;}
template <class T>
void QSort(T L[], int low, int high)//比较函数
{int pivotloc;if (low < high){pivotloc = Partition(L, low, high);QSort(L, low, pivotloc - 1);QSort(L, pivotloc + 1, high);}
}template<class T>
void QuickSort(T L[],int max)//快速排序
{QSort(L, 1, max);
}
我们这样就完成了外部排序,接下来要做的是如何归并,我们首先得开个500大小的数组存每个文件的第一个数据,然后在开一个500的文件流数组便于读数据。
这里可能会有疑问为什么只能开500个文件流?
因为文件流最大只能同时开508个,因此我们所用的文件流最大只能开到500,因为正好整除,这也是第二次只分500个文件的原因。
接下来就是如何保证每次输入到目标文件里是最小的,我这里有三种方法(result.h):
第一种方案:我们可以每次遍历数组找到最小的然后写到文件里,再上对应文件中读入下一个数据,再遍历,一次类推,代码如下:
#pragma once
#include运行结果如下:
我们发现其实并不快,那么是为什么影响其速度呢,那就是每次都得做n次比较,因此比较浪费空间,因此想到了第二种方法。
第二种方案:既然比较浪费了这么多时间做比较,我们可以第一遍将数组排成有序的每次将数组中的第一个元素写到目标文件中,然后新加的元素做二分插入排序,以此类推,这样最坏是n次比较,最好1次比较,代码如下:
#pragma once
#includeif (j == 30){fprintf_s(fp1, "\n");j = 1;}else{j++;}tmp = b[1].flag;if (tmp > 0){if (!feof(fp[tmp])){fscanf_s(fp[tmp], "%d", &b[1].a);flag1 = 1;}else{for (i = 1; i < MAX1; i++){if (fp[i] != NULL){fscanf_s(fp[i], "%d", &b[1].a);b[1].flag = i;break;flag1 = 1;}}if (!flag1){break;}}InsertSort(b,MAX1);}}for (i = 2; i < MAX1; i++){fprintf_s(fp1, "%d ", b[i].a);//cout << b[1].a<}fclose(fp1);for ( i = 1; i < MAX1; i++){fclose(fp[i]);}return 0;
}
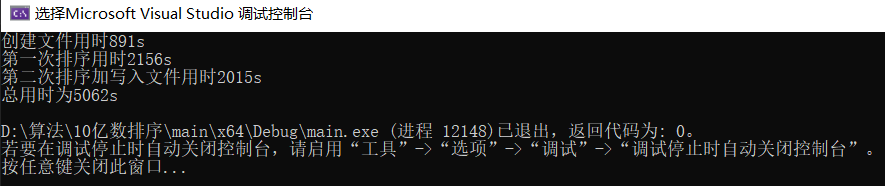
运行结果为:
从运行结果发现性能提高了,但是并未提高太多(这是最好的一次运行结果),那么是为什么导致的呢,这是由于虽然比较少了,但是数据交换次数比较多,这样会占很多的时间和空间,因此笔者做了很多构想,最后想出第三种方案。
第三种方案:那么我们如何将前两种方法综合起来呢,既不做如此多的比较,又使用较少的交换次数,其实这个是最关键的思想,最终我想到了用堆排序的方法,这样500大小的数组最多比较27次,做1次交换,性能大大提高,当我们其中的一个文件读完之后,我们可以将数组头和尾交换,然后数组长度减一,直到数组有效长度为0,代码如下:
#pragma once
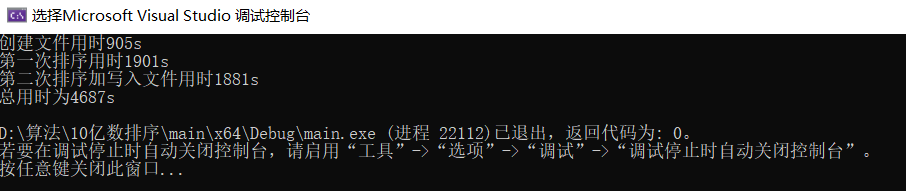
#include运行结果为:
从运行结果可以看出此方法的性能是最好的,综合了前两种方法的特点,既没有比较太多的次数,也没有做太多次的数据交换,所以整体性能最好
至此我们就将10亿随机数排成有序的了。
源代码已上传github:源代码
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!