数据库课设——最佳配对
一、实验目的和要求
问题描述:
羽毛球队有男女运动员各n人。给定2 个n×n矩阵P和Q。P[i][j]是男运动员i和女运动员j配对组成混合双打的男运动员竞赛优势;Q[i][j]是女运动员i和男运动员j配合的女运动员竞赛优势。由于技术配合和心理状态等各种因素影响,P[i][j]不一定等于Q[j][i]。男运动员i和女运动员j配对组成混合双打的男女双方竞赛优势为P[i][j]*Q[j][i]。设计一个算法,计算男女运动员最佳配对法,使各组男女双方竞赛优势的总和达到最大。
编程任务:
设计一个优先队列式分支限界法,对于给定的男女运动员竞赛优势,计算男女运动员最佳配对法,使各组男女双方竞赛优势的总和达到最大。
数据输入:
第一行有1 个正整数n (1≤n≤20)。接下来的2n行,每行n个数。前n行是p,后n行是q。
结果输出:
将计算出的男女双方竞赛优势的总和的最大值输出。
样例输入:
3
10 2 3
2 3 4
3 4 5
2 2 2
3 5 3
4 5 1
样例输出:52
- 实验环境
Codeblocks
- 解题思路
1、求问题的解空间
对于n个男运动员,从第1个开始搭配女运动员:第1个有n种搭配方法,第2个有n-1种搭配方法……第n个有n-(n-1)种搭配方法;根据问题给出的示例:输入n的值为3,表示男女运动员各有3名;
男运动员 1 2 3按顺序搭配女运动员,他们分别对应的女运动员可以是:
女运动员 1 2 3、1 3 2、2 1 3、2 3 1、3 1 2、3 2 1
所以其解空间是{(1,2,3),(1,3,2),(2,1,3),(2,3,1),(3,1,2),(3,2,1)},整个问题可看成是1,2,3的全排列问题。
对样例数据分析,得到以下的排列树:
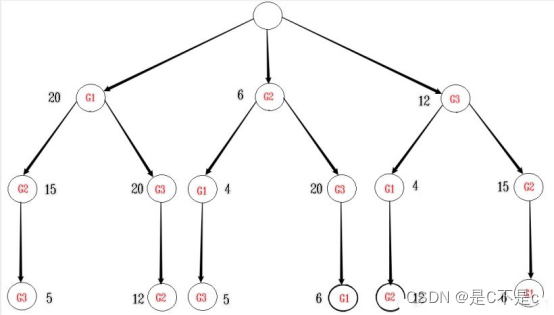
注:本题采用的是男运动员选女运动员的方法,这样就构成了一棵排列树。G表示女运动员,排列树的层数表示男运动员。如第一层的G1=20表示,男运动员1号选女运动员1号的男女双方竞赛优势为20。
2、用深度优先的搜索策略搜索整个解空间
最初的想法为:
用一个数组x记录可行解,并且赋初值为{0,1,2…n},x[i]表示第i个男生配对的女生号;所以第i个男生与第x[i]个女生双方竞赛优势为P[i-1][x[i]-1]*Q[x[i]-1][i-1];
用t表示递归深度,初值为1,表示第1个男生开始搭配;t可以由n来控制。
当t>n时,表示算法已搜索到叶子结点,此时根据x的记录计算男女双方竞赛优势的总和s,算法如下:
P[j][x[j+1]-1]*Q[x[j+1]-1][j]表示第j+1个男运动员与第x[j+1]个女运动员配对组成混合双打的男女双方竞赛优势int s=0; //记录当前男女双方竞赛优势总和,计算前值为0for(int j=0;j并判断s是否大于当前记录的男女双方竞赛优势的总和的最大值sum,若s>sum,则给sum赋值s;
当t<=n时,表示还没有搜索到叶子结点,则需要继续往下搜索,从i=t开始搜索至i=n;
for(int i=t;i<=n;i++){Swap(&x[t],&x[i]); //交换x[t]和x[i]的值,第t和第i个男运动员交换搭档//没有约束函数和限界函数Backtrack(t+1); //进行第t+1个男运动员配对Swap(&x[t],&x[i]); //交换回来它们的值,以便于与另外的另外的男运动员交换}之后优化后的结果如下:
int ctn = 0; //剪枝函数:之前t个已匹配好的男女运动员的sum与之后的 t->n-1 个男匹配女的最大值加起来与已经得到的Max比较,若前者<=Max,剪枝for (int i = t;i < n;i++) //求t及t之后男生匹配女生的最大值的和ctn += maxSum[i];if (sum + ctn < Max) //若从第t组->第n组,当前搜索sum加上假设匹配后的最大值cxn,仍然小于Max ,就需要剪枝了,则Max为已经求得的最大值return;for (int i = 0;i < n;i++) //若cxn>=Max,要探索子树。从第t个男生开始匹配,找未匹配的女生{if (!book[i]) //第 i 个女生未匹配{book[i] = 1; //第 t 个男生匹配女生isum += data[t][i]; //加上男生t与女生i的男女双方竞赛优势dfs(t + 1); //为第i+1个男生匹配book[i] = 0; //若第 t 个男生匹配女生i得到的sum不大于Max,则回溯sum -= data[t][i];}}
四、测试及结果
五、实验收获
通过这次实验,基本上掌握了用回溯法解题的算法框架,首先要理解问题,找出问题的解空间;其次是根据解空间画出解空间树;最后按照深度优先的搜索策略来搜索整棵树来得到最优解。实验让我更进一步地理解了回溯法的深度优先搜索策略,从根结点出发,根结点成为活结点,成为当前的扩展结点,搜索向纵深方向移至一个新结点,这个新结点会成为新的活结点,在当前扩展结点处不能再向纵深方向移动,当前扩展结点就成为死结点;此时往回移动至最近的一个活结点,就这样递归地在解空间中搜索,直到找到所要求的解或解空间中已无活结点为止。
六、附录(源代码)
#include
using namespace std;int n;
int boy[21][21], girl[21][21]; //分别用于存放男、女运动员的竞赛优势
int Max = INT_MIN; //Max代表男女双方竞赛优势的总和的最大值
int sum = 0; //sum为临时求和
int data[21][21]; //data[i][]用于存放男运动员 i 配对后的双方竞赛优势
int maxSum[21]; //记录每个男生匹配后可达到的最大双方竞赛优势
int book[21]; //用于标记女运动员是否已匹配:book[0]未匹配;book[1]匹配void dfs(int t)
{if (t >= n) //t到达n之后,代表全部标记访问了,得到了最大值{Max = max(Max, sum);return;}int ctn = 0; //剪枝函数:之前t个已匹配好的男女运动员的sum与之后的 t->n-1 个男匹配女的最大值加起来与已经得到的Max比较,若前者<=Max,剪枝for (int i = t;i < n;i++) //求t及t之后男生匹配女生的最大值的和ctn += maxSum[i];if (sum + ctn < Max) //若从第t组->第n组,当前搜索sum加上假设匹配后的最大值cxn,仍然小于Max ,就需要剪枝了,则Max为已经求得的最大值return;for (int i = 0;i < n;i++) //若cxn>=Max,要探索子树。从第t个男生开始匹配,找未匹配的女生{if (!book[i]) //第 i 个女生未匹配{book[i] = 1; //第 t 个男生匹配女生isum += data[t][i]; //加上男生t与女生i的男女双方竞赛优势dfs(t + 1); //为第i+1个男生匹配book[i] = 0; //若第 t 个男生匹配女生i得到的sum不大于Max,则回溯sum -= data[t][i];}}
}int main()
{cin >> n;for (int i = 0;i < n;i++) //输入男运动员的竞赛优势{for (int j = 0;j < n;j++)cin >> boy[i][j];}for (int i = 0;i < n;i++) //输入女运动员的竞赛优势{for (int j = 0;j < n;j++)cin >> girl[i][j];}for (int i = 0;i < n;i++){for (int j = 0;j < n;j++){data[i][j] = boy[i][j] * girl[j][i]; //对每个男生都求男女双方竞赛优势,则能得到i*j种结果(涵盖了P[i][j]*Q[j][i]与Q[i][j]*P[j][i])maxSum[i] = max(maxSum[i], data[i][j]); //记录每个男生匹配后可达到的最大双方竞赛优势,用于后面的剪枝}}dfs(0);cout << Max << endl;return 0;
}
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!