格密码学习记录(二)
1. 格理论中的基本概念和困难问题




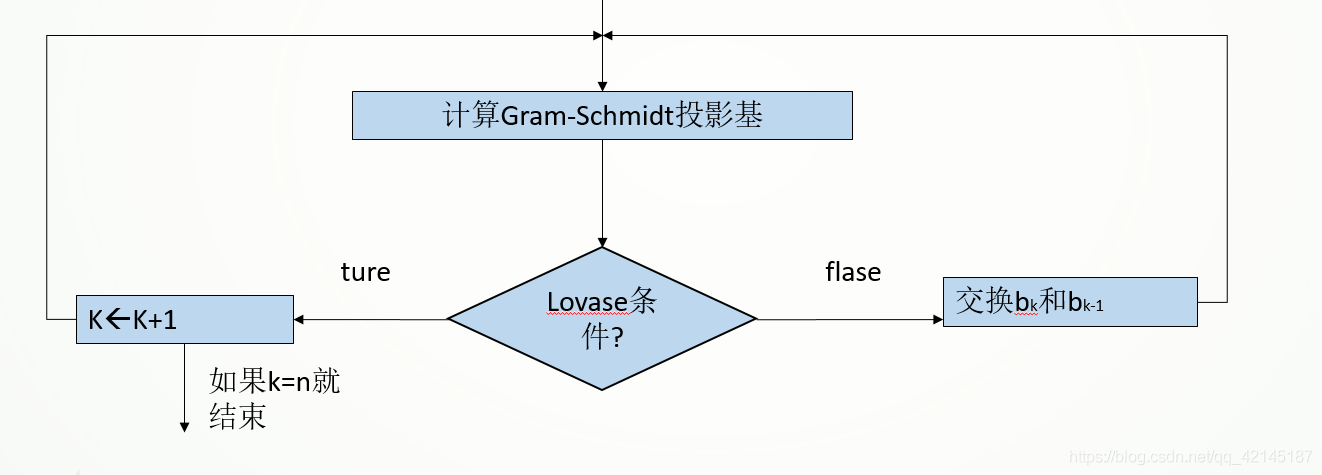
2.LLL算法
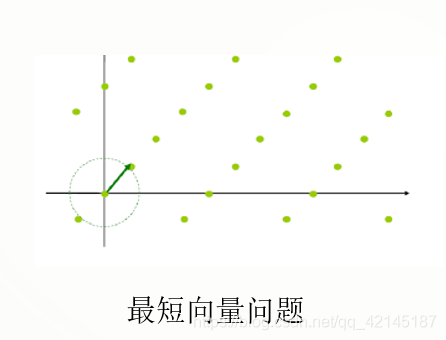
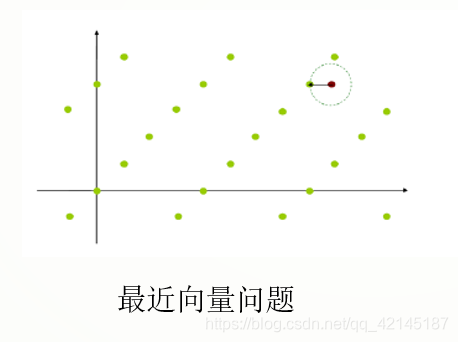
在高维的空间中,求解最短向量问题无法实现,我们只能求出近似的最短向量问题。
第一个也是最著名的求解近似最短向量问题的算法是由H. Lenstra, A. Lenstra, Lovasz 在1982 年提出的 LLL 算法。
从格的任意基开始,LLL算法计算出一个较短的格向量组成的新的基,这个新的基被称为简化基。约减的主要目的是将这组任意给定的基转化为一组正交性较好的优质基,并使得这个优质基中的各个向量尽量最短。
定义:格的LLL化简基是格元素的一个有序基{b1,b2,,,,bn},其中的施密特正交投影基以及投影系数必须满足以下 的条件:
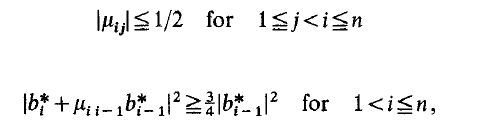
在高维的空间中,我们只能求出近似的最短向量问题,不能求出准确的最短向量问题
条件一说明了向量bi必须接近于正交
条件二:格L 就最短向量组的范数而言的界

本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!