c语言实现数据结构--深入了解字典树和双数组字典树
这是字符串匹配的方法的第二部分,个人对于数据结构还是学习阶段,希望各位大佬来指导,笔芯
目录
字典树
一种误区
节点
双数组字典树
完全二叉树对于空间的节省
双数组字典树
字典树
字典树(Trie 树),也叫单词查找树,用于单词查找、字符串的排序等。
一种误区
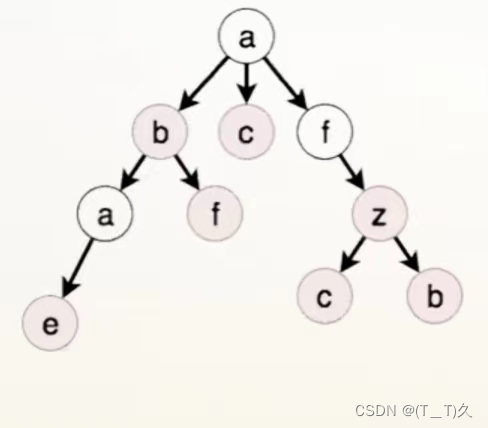
像图片中的这一类表示是错误的,字典树是用边来表示或者存储一个字母的,而不是类似于图中的节点。
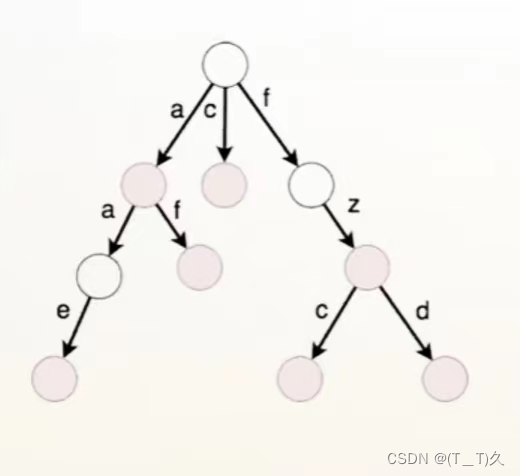
如上图,真正的字典树应该是字母被标记在边上,也就是说一条边代表一个字母。
节点
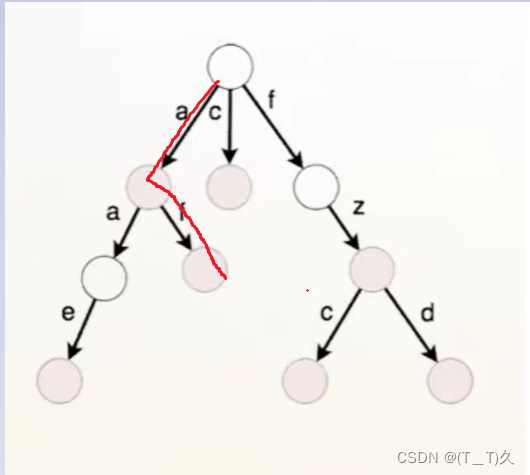
在此图中,按照红线这条路径,走到最下面,走到深颜色的节点 ,这条路径所形成的前缀就是af,从根节点到当前节点路径上面的字符组合在一起,就是所要存储的单词。看一下上图,一共存在深颜色和浅颜色的节点,深色节点代表当前路径上的单词已经是一个独立的单词。
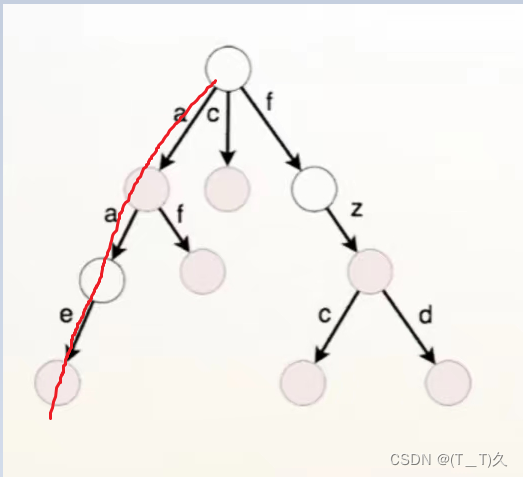
比如我们往字典树中插入了一个aae这个单词,当遍历这个字典树时通过aa可以走到一个合法的节点,但是此时是浅色的节点,我们就可以知道aa在这个字典树中并不是一个独立的单词,即不存在于这个字典树。

字典树中可以写出这些单词,我们把每个单词当作遍历的一条路径,会发现我们就是按照字典序走的,就可以基于此进行一个排序,可以降低好多时间复杂度,因为可以没有基于比较过程,这就是为啥用作字符串排序。
代码演示如下:
#include
using namespace std;
typedef long long ll;
#define BASE 26
#define BASE_LETTER 'a'typedef struct Node {int flag;struct Node *next[BASE];
} Node;Node *getNewNode() {Node *p = (Node *)calloc(sizeof(Node), 1);return p;
}inline int code(char ch) {return ch - BASE_LETTER;
}void insert(Node *root, char *str) {Node *p = root;for (int i = 0; str[i]; i++) {if (p->next[code(str[i])] == NULL) p->next[code(str[i])] = getNewNode();p = p->next[code(str[i])];}p->flag = 1;return ;
}int query(Node *root, char *str) {Node *p = root;for (int i = 0; str[i]; i++) {p = p->next[code(str[i])];if (p == NULL) return 0;}return p->flag;
}
void output(Node *root, int k, char *buff) {if (root == NULL) return ;if (root->flag) printf("%s\n", buff);for (int i = 0; i < BASE; i++) {buff[k] = BASE_LETTER + i;buff[k + 1] = '\0';output(root->next[i], k + 1, buff);}return ;
}void clear(Node *root) {if (root == NULL) return ;for (int i = 0; i < BASE; i++) {clear(root->next[i]);}free(root);return ;
}int main() {char str[1000];int n;Node *root = getNewNode();scanf("%d", &n);for (int i = 0; i < n; i++) {scanf("%s", str);insert(root, str);}output(root, 0, str);while (~scanf("%s", str)) {printf("query %s, result = %s\n", str, query(root, str) ? "Yes" : "No");}return 0;
} 双数组字典树
双数组字典树本质上还是字典树,不过是表示方式不同。
可以看出之前字典树浪费了好多字节,边的存储和浪费非常多,那么我们如何对这个结构做出存储空间上的优化。
完全二叉树对于空间的节省

这是一个完全二叉树,利用了一段连续的存只存储了数据,没有存储指针,从而节省了大量的空间。即记录转成计算。
如果我们把关于边的信息参考完全二叉树,由记录转成计算,字典树就会节省大量空间。
双数组字典树

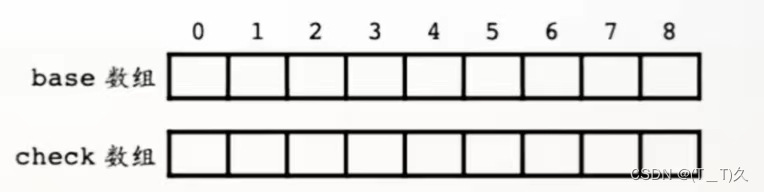
我们的字典树就是利用两个数组---base数组和check数组。base数组里面记录的值就是将字典树转化成计算式的关键。
base数组记录了一种找到子节点的关键数值,check数组里面记录的是该编号的父节点,例如:base[8]=1,就是节点8的父节点是编号为一的节点
base[i]+边上字符的编码就是相应的“儿子”。
举个例子:a映射到0,b映射到1,c映射到2,d映射到3.
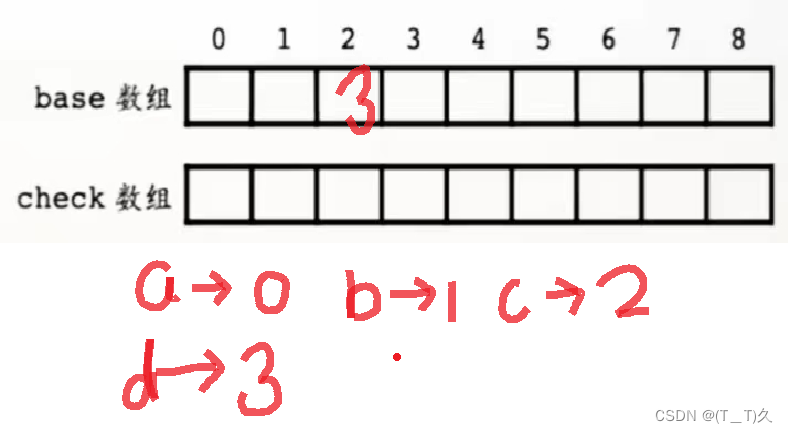
假设base[2]=6,怎样知道下面有d(编码是3)这条边?

即base数组是计算的中间量,那么我们可以利用base数组构建一棵树。但是这棵树是有冲突的,如下:
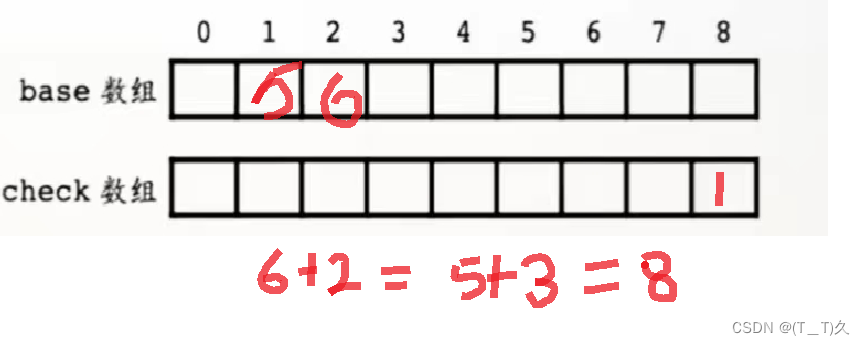
那么此时我们可以知道1号节点的编码为2的边和2号节点的编码为3的边得出的节点编号都为8,但看一下check数组,base[8]=1,即8号节点的父节点是1,同时还说明2号节点没有编码为3的边。
看到这里,我们可以知道这个树不大好插入,也不大好修改删除。
看一下这个图,有深颜色和浅颜色的节点,那么怎么表示呢?
答案是符号的正负,节点存储的数据如果是正的,就独立成词,反之不独立成词,(反过来也可以)。注意一点,正负作为一个标准,我们就要特别关注一个自然数“0”,我们check数组存放的是父节点的编号,不能是0的话,我们的存储是不是就是需要从1开始,答案是肯定的。
问题来了,在对check数组初始化时,check一开始是不是全是0,那么意思就是check[i]=0,是不是就是意味着check此处没有被占用,即i这个节点没有被用到,因为用到了一定会有一个非零的父节点的编号。
#include
using namespace std;
typedef long long ll;
#define BASE 26
#define BEGIN_LETTER 'a'typedef struct Node {int flag;struct Node *next[BASE];
} Node;typedef struct DATrie {int *base, *check;int root, size;
} DATrie;DATrie *getDATrie(int n) {DATrie *tree = (DATrie *)calloc(sizeof(DATrie), 1);tree->root = 1;tree->size = n;tree->base = (int *)calloc(sizeof(int), n);tree->check = (int *)calloc(sizeof(int), n);tree->check[tree->root] = 1;return tree;
}Node *getNewNode() {Node *p = (Node *)calloc(sizeof(Node), 1);return p;
}int insert(Node *root, const char *str) {int cnt = 0;Node *p = root;for (int i = 0; str[i]; i++) {int ind = str[i] - BEGIN_LETTER;if (p->next[ind] == NULL) p->next[ind] = getNewNode(), cnt += 1;p = p->next[ind];}p->flag = 1;return cnt;
}void clear(Node *root) {if (root == NULL) return ;for (int i = 0; i < BASE; i++) {clear(root->next[i]);}free(root);return ;
}int getBaseValue(Node *root, DATrie *tree) {int base = 0, flag;do {flag = 1;base += 1;for (int i = 0; i < BASE; i++) {if (root->next[i] == NULL) continue;if (tree->check[base + i] == 0) continue;flag = 0;break;}} while (!flag);return base;
}int buildDATrie(int ind, Node *root, DATrie *tree) {int base = tree->base[ind] = getBaseValue(root, tree);int ans = ind;for (int i = 0; i < BASE; i++) {if (root->next[i] == NULL) continue;tree->check[base + i] = ind;}for (int i = 0; i < BASE; i++) {if (root->next[i] == NULL) continue;int temp = buildDATrie(base + i, root->next[i], tree);if (temp > ans) ans = temp;}if (root->flag) tree->check[ind] = -tree->check[ind];return ans;
}int query(DATrie *tree, const char *str) {int p = tree->root;for (int i = 0; str[i]; i++) {int ind = str[i] - BEGIN_LETTER;if (abs(tree->check[tree->base[p] + ind]) != p) return 0;p = tree->base[p] + ind;}return tree->check[p] < 0;
}void clearDA(DATrie *tree) {if (tree == NULL) return ;free(tree->base);free(tree->check);free(tree);return ;
}int main() {int n, cnt1 = 1, cnt2;char str[100];scanf("%d", &n);Node *root = getNewNode();while (n--) {scanf("%s", str);cnt1 += insert(root, str);}DATrie *tree = getDATrie(cnt1 * BASE + 5);cnt2 = buildDATrie(tree->root, root, tree) + 1;while (~scanf("%s", str)) {printf("search %s, result = %s\n", str, query(tree, str) ? "YES" : "NO");}int mem1 = cnt1 * sizeof(Node), mem2 = cnt2 * sizeof(int) * 2 + sizeof(int) * 2;printf("Trie memory : %d Bytes\n", mem1);printf("Double Array Trie memory : %d Bytes\n", mem2);printf("memory rate : %.4lf%%\n", 1.0 * mem2 / mem1 * 100);clearDA(tree);clear(root);return 0;
} 学习数据结构要跟着网课或者书练,所以可以去力扣或者牛客找相应的题做
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!