Logistic Regression（逻辑回归）

Logistic回归思想：

Logistic 回归是与线性回归相对应的一种分类方法，是一种广义线性回归模型(generalized linear model)。该算法的基本概念由线性回归推导而出，比如上图，如果直接尝试线性拟合或是直接用单位阶跃来判断其类别的话，因变量为二分类变量，某个概率作为方程的因变量估计值取值范围为0-1，但是，方程右边取值范围是无穷大或者无穷小，会造成方程二边取值区间不同和普遍的非直线关系（单纯的均方误差损失函数的话），即会变成非凸函数（non-convex function），这就意味着可能会有许多局部最小值。
此时引入Logistic 回归通过 Logistic 函数（即 Sigmoid 函数），它将自变量与因变量的关系假定是S行的形状，当自变量很小时，机率值接近为零；当自变量值慢慢增加时，机率值沿着曲线增加，增加到一定程度时，曲线协 率开始减小，故机率值介于0与1之间。从而预测映射到 0 到 1 中间，因此预测值就可以看成某个类别的概率。

由于线性回归是连续的，所以可以用均方误差和来做损失函数J。而逻辑回归是离散的，只能使用交叉熵的方式，再采用最大似然法来采样得到方便求解的损失函数。
首先由可能出现的结果分类0，1可得： P ( y = 1 ∣ x , w ) = h w ( x ) P(y=1|x,w) = h_{w}(x) P(y=1∣x,w)=hw​(x) P ( y = 0 ∣ x , w ) = 1 − h w ( x ) P(y=0|x,w ) = 1- h_{w}(x) P(y=0∣x,w)=1−hw​(x)
于是可得，意味着要将这两类的差距分的越大越好： P ( y ∣ x , w ) = h w ( x ) y ( 1 − h w a ( x ) ) 1 − y P(y|x,w ) = h_{w}(x)^y(1-h_{wa}(x))^{1-y} P(y∣x,w)=hw​(x)y(1−hwa​(x))1−y
但是这样的函数很难求导，于是尝试使用关于分布的采样来求参数w–似然函数为： L ( w ) = ∏ i = 1 m ( h w ( x ( i ) ) ) y ( i ) ( 1 − h w ( x ( i ) ) ) 1 − y ( i ) L(w) = \prod\limits_{i=1}^{m}(h_{w}(x^{(i)}))^{y^{(i)}}(1-h_{w}(x^{(i)}))^{1-y^{(i)}} L(w)=i=1∏m​(hw​(x(i)))y(i)(1−hw​(x(i)))1−y(i)

取对数（取对数并不会改变函数的极值，反而会使求导更方便）即可以得到损失函数： J ( w ) = − l n L ( w ) = − ∑ i = 1 m ( y ( i ) l o g ( h w ( x ( i ) ) ) + ( 1 − y ( i ) ) l o g ( 1 − h w ( x ( i ) ) ) ) J(w) = -lnL(w) = -\sum\limits_{i=1}^{m}(y^{(i)}log(h_{w}(x^{(i)}))+ (1-y^{(i)})log(1-h_{w}(x^{(i)}))) J(w)=−lnL(w)=−i=1∑m​(y(i)log(hw​(x(i)))+(1−y(i))log(1−hw​(x(i))))
同样的，加上正则化项后用对应方法解出即可。与线性回归的梯度下降不一样，最大似然估计求解参数可以理解成是对样本的m次抽样，当独立同分布的m次抽样同时发生时（所以要连乘）进行估计。【虽然服从正态分布的矩估计和最大似然是一样的】

由于需要差距越“大”越好，故整个损失函数需要求的是最大值，在求解参数时需要使用梯度上升，以上最终的损失函数加上了负号，可统一变成梯度下降方式求解。
@@@对这个损失函数的另一种理解是：

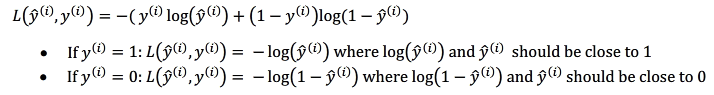
即如果实际值是1，需要最小化的损失函数为-logy，那么意味着预测值y要尽可能的大，尽可能的趋近于1。同理实际上为0，预测会尽可能的小。

另外对于交叉熵 L = − y l o g ( y ′ ) L=-ylog(y') L=−ylog(y′)来说，它的梯度求解会变成 − y y ′ - \frac{y}{y'} −y′y​，它其实衡量了这两个概率分布的接近程度。

为什么要使用交叉熵作为损失函数而不是普通的平方损失？
在线性回归中使用了平方损失，而逻辑回归中使用了交叉熵。

• 首先平方误差损失容易理解，直接衡量了模型的输出和标准值在数值上的差距，其实在做逻辑回归的二分类问题（二值y为0，1）上同样也是可以使用平方误差的。
• 但是平方误差显然更加适合连续型的数据，原因在于平方误差对所有的输出都一视同仁，尝试逼近所有值，所以会关注每一个预测值，使更平均。
• 而交叉熵函数只对正确的分类看重，尝试把所有类别之间的关系划得很清楚，所以它的梯度只与正确预测的结果有关，而不像平方误差的梯度与错误分类的有关。（实际上平方误差不仅想让正确分类越大，而且想要错误分类更加的平均，这一点比较画蛇添足，实用性不强）所以在分类问题上，交叉熵损失函数的使用更加的有针对性，效果往往更好。
• 信息论角度的解释（见文末对损失函数的整理）

附：在多层神经网络中有时候也使用交叉熵
神经网络中，单层的往往使用了Sigmoid作为激活函数，在多层中为了应对梯度消失问题便换用了ReLU激活函数，DropOut，甚至ResNet等方法，损失函数也一般就使用了平方损失。在一些场景中，也会使用交叉熵，原因在于：

• 对于平方损失在更新w，b时候，w,b的梯度跟激活函数的梯度成正比，激活函数梯度越大，w,b调整就越快，训练收敛就越快，但是Simoid函数在值非常高时候，梯度是很小的，比较平缓。（于是可以用ReLU初步解决）
• 对于交叉熵在更新w,b时候，w,b的梯度跟激活函数的梯度没有关系了，而是预测值跟实际值差距，如果差距越大，那么w,b调整就越快，收敛就越快。
• 二次幂的代价函数存在很多局部最小点，会震动，而交叉熵就不会，会平稳的收敛。

所以选用指南就是：先看连续与离散，再看函数是否有凸函数性质，方不方便求求导。然后，看结果…谁效果好就选谁。

算法实现：（Python）

def sigmoid(inX):return 1.0/(1+exp(-inX))def stocGradAscent(dataMatrix, classLabels, numIter=150):#随机梯度上升（如使用梯度下降需要加负号）m,n = shape(dataMatrix)weights = ones(n) for j in range(numIter):dataIndex = list(range(m))for i in range(m):alpha = 4/(1.0+j+i)+0.0001 #控制收敛，避免数据高频波动randIndex = int(random.uniform(0,len(dataIndex)))#随机更新。减少数据周期性波动h = sigmoid(sum(dataMatrix[randIndex]*weights))error = classLabels[randIndex] - hweights=weights+dot(alpha,dot(error,dataMatrix[randIndex])del(dataIndex[randIndex])return weights

##高频波动是由于数据集自身的分布可能不是完全线性可分的，那么逻辑回归有时候不能正确的分类，容易出现反复的波动，特别是数据量很大的时候。所以会控制alpha，即梯度的步长，它会随着迭代次数而减少，同样的，随机选择样本更新梯度会使收敛会更快。

Logistic回归实质
发生概率除以没有发生概率再取对数。就是这个不太繁琐的变换改变了取值区间的矛盾和因变量自变量间的曲线关系。究其原因，是发生和未发生的概率成为了比值 ，这个比值就是一个缓冲，将取值范围扩大，再进行对数变换，整个因变量改变。不仅如此，这种变换往往使得因变量和自变量之间呈线性关系，这是根据大量实践而总结。所以，Logistic回归从根本上解决因变量要不是连续变量怎么办的问题。还有，Logistic应用广泛的原因是许多现实问题跟它的模型吻合。例如一件事情是否发生跟其他数值型自变量的关系。

缺点：对模型中自变量多重共线性较为敏感，例如两个高度相关自变量同时放入模型，可能导致较弱的一个自变量回归符号不符合预期，符号被扭转。可以使用逻辑回归结合L2正则化来解决，不过如果要得到一个简约模型，L2正则化并不是最好的选择，因为它建立的模型涵盖了全部的特征。​需要利用因子分析或者变量聚类分析等手段来选择代表性的自变量，以减少候选变量之间的相关性；当特征空间很大时，逻辑回归的性能不是很好；不能很好地处理大量多类特征或变量；对于非线性特征，需要进行转换。

SVM、LR、决策树的选择？
首先就应该选择的逻辑回归，如果它的效果不怎么样，也可以作为基准来参考，然后再试决策树（随机森林）是否可以大幅度提升模型性能。如果也不会当做最终模型，移除噪声变量也是很好的，如果特征的数量和观测样本特别多，当资源和时间充足时，应该使用SVM。


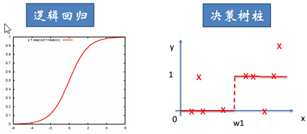
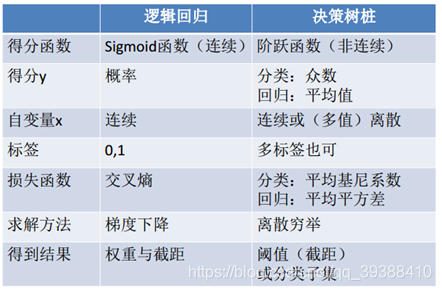
LR和SVM相比。损失函数一个是logistical loss，一个是hinge loss，目的都是增加对分类影响大的数据点的权重；SVM只考虑支持向量，也就是和分类最相关的少数点去学习调整分类器，而逻辑回归通过非线性映射大大减小了离分类点远的权重；LR模型简单，好解释，大规模线性时很方便，SVM的计算稍稍麻烦；LR能做的SVM都能做，但准确率上不一定好，SVM能做的LR不一定做的到。

为什么不直接用阶跃而要用Sigmoid函数？
阶跃函数虽然很直观的能够划分类别，但是它非凸、非光滑，所以很难优化和求解。而Sigmoid除了自己是连续光滑无限阶都可导，能够完美的完成映射任务。当然除了Sigmoid，还有其他很多的激活函数，更多可以参考神经网络。

狭义线性模型与广义线性模型
逻辑回归本身是从线性模型推导而来，是广义的线性模型。这里的广义是值在经过激活函数后，是狭义下因变量的误差必须满足正态分布，变成了满足指数族分布就行了，扩展了其使用范围。

为什么逻辑回归要对特征进行离散？

• 为了完成非线性的任务，增加模型的表达能力。
• 鲁棒性。特别是对于异常数据也具有包容性（如年龄1000岁在年龄“老”这以离散的空间中），所以模型也会更加的稳定
• 特征离散化，简化了逻辑回归模型的作用，降低了模型过拟合的风险。

逻辑回归的优点：
以概率输出结果，而不仅仅是以0，1来判定，可解释性强，可控度高。训练快，做feature engineering之后效果很好。也因为是概率，可以用来做ranking model。

LR的实际应用场景

• CRT预估/Learning to rank/分类。不论现在技术上有多花哨，在各种大厂中的推荐系统中绝对少不了LR。

logistic应用：
看一下线性回归和逻辑回归的比较：

import numpy as np
import matplotlib.pyplot as pltfrom sklearn import linear_modelxmin, xmax = -5, 5
n_samples = 100
np.random.seed(0)
X = np.random.normal(size=n_samples)#有噪声的数据集
y = (X > 0).astype(np.float)
X[X > 0] *= 4
X += .3 * np.random.normal(size=n_samples)X = X[:, np.newaxis]
clf = linear_model.LogisticRegression(C=1e5)#clf
clf.fit(X, y)plt.figure(1, figsize=(4, 3))
plt.clf()
plt.scatter(X.ravel(), y, color='black', zorder=20)
X_test = np.linspace(-5, 10, 300)def model(x):return 1 / (1 + np.exp(-x))
loss = model(X_test * clf.coef_ + clf.intercept_).ravel()
plt.plot(X_test, loss, color='red', linewidth=3)ols = linear_model.LinearRegression()#ols
print(ols)
ols.fit(X, y)
plt.plot(X_test, ols.coef_ * X_test + ols.intercept_, linewidth=1)
plt.axhline(.5, color='.5')plt.ylabel('y')
plt.xlabel('X')
plt.xticks(range(-5, 10))
plt.yticks([0, 0.5, 1])
plt.ylim(-.25, 1.25)
plt.xlim(-4, 10)
plt.legend(('Logistic Regression Model', 'Linear Regression Model'),loc="lower right", fontsize='small')
plt.show()

关于损失函数
线性回归 的损失函数是均方误差（Mean Squared Error，MSE），算是最常用的一种损失函数，直观上是预测与真实值之间的差异。当时是直接使用了MSE这一形式，实际上也可以从概率的角度推得。

• 1假设模型预测值和真实值之间的误差服从标准高斯分布（$\mu =0,\sigma =1$），那么给定一个xi，模型输出真实值yi的概率为： p ( y i ∣ x i ) = 1 2 π e x p ( − ( y i − y ) 2 2 ) p(y_i|x_i)=\frac{1}{\sqrt{2\pi}}exp(-\frac{(y_i-y)^2}{2}) p(yi​∣xi​)=2π ​1​exp(−2(yi​−y)2​)
• 进一步假设所有样本点都相互独立，那么似然likelihood一下： L ( x , y ) = ∏ i = 0 N 1 2 π e x p ( − ( y i − y ) 2 2 ) L(x,y)=\prod_{i=0}^N \frac{1}{\sqrt{2\pi}}exp(-\frac{(y_i-y)^2}{2}) L(x,y)=i=0∏N​2π ​1​exp(−2(yi​−y)2​)
• 取对数： L ( x , y ) = − N 2 l o g 2 π − 1 2 ∑ i = 1 N ( y i − y ) 2 L(x,y)=-\frac{N}{2}log2\pi-\frac{1}{2}\sum_{i=1}^N(y_i-y)^2 L(x,y)=−2N​log2π−21​i=1∑N​(yi​−y)2然后去掉第一项的无关项，再变成负似然对数就是一般的MSE了。这也说明了模型输出与真实值的误差服从高斯分布的假设下，MSE和极大似然估计的本质是一样的（理解为矩估计和极大似然估计）。因此！在这个假设能够被满足的条件下（比如回归），这个损失函数就很好，而在分类，MSE不是一个好选择。

另外和MSE很像的平均绝对误差损失（Mean Absolute Error Loss，MAE）也差不多，它的概率推导是在假设模型预测与真实值之间的误差服从拉普拉斯分布（$\mu =0,b=1$）
p ( y i ∣ x i ) = 1 2 e x p ( − ∣ y i − y ∣ ) p(y_i|x_i)=\frac{1}{2}exp(-|y_i-y|) p(yi​∣xi​)=21​exp(−∣yi​−y∣)然后再同理似然一下也是一样的。
和l1、l2的对比类似，MAE和MSE对比，MSE比MAE收敛更快（MSE梯度为-y，MAE是±1），但MAE对离群点更鲁棒（MSE平方了之后，离群点outlier的损失会很大）。所以，自然产生了能结合这两点的损失函数Huber Loss：在误差接近0的时候用MSE（使梯度可导更稳定），误差大的时候用MAE（降低离群点的影响），不过确实需要额外设置一个平衡这两者的超参。

交叉熵损失如本文开头所推导，是适用于分类环境下的损失函数。但在处理多分类的时候，需要使用softmax，即把预测的类别从原先的二分类变成one-hot向量，然后Sigmoid换成Softmax，将分数映射到(0，1)就可以了。至于为什么在分类中不用均方差损失，除了文中的解释、假设条件不满足外，还可以从信息论角度探讨（信息论基础在这里）:

• 对于样本 x i x_i xi​存在一个最优分布 y i ∗ y_i^* yi∗​，能够真实表明这个样本属于各个类别的概率，那么模型需要做的就是尽可能的逼近这个分布。评价分布的KL散度就可以出场了： K L ( y i ∗ , y i ) = ∑ k = 1 K y i ∗ l o g ( y i ∗ ) − ∑ k = 1 K y i ∗ l o g ( y i ) KL(y_i^*,y_i)=\sum_{k=1}^Ky_i^*log(y_i^*)-\sum_{k=1}^Ky_i^*log(y_i) KL(yi∗​,yi​)=k=1∑K​yi∗​log(yi∗​)−k=1∑K​yi∗​log(yi​)然后最小化它，就和普通交叉熵的式子是一样的了。

关于二分类函数，还可以使用 合页损失（Hinge Loss），它适合于maximum-margin分类，如SVM的损失函数本质上就是Hinge+L2。它的公式是： H i n g e = ∑ i = 1 N m a x ( 0 , 1 − s g n ( y i ) y ) Hinge=\sum_{i=1}^Nmax(0,1-sgn(y_i)y) Hinge=i=1∑N​max(0,1−sgn(yi​)y)y的预测是1时，它对负值会有很大惩罚，对（0，1）区间有小的惩罚，所以直觉上它是想找到一个决策边界，使所有数据点被这个边界正确的，高置信度的分类。

Log-Cosh损失 常用于回归问题。是比L2损失函数更平滑的损失函数，它计算的是预测误差的双曲余弦的对数： L = ∑ i = 1 n l o g ( c o s h ( y i ∗ − y i ) ) L=\sum_{i=1}^n log(cosh(y_i^*-y_i)) L=i=1∑n​log(cosh(yi∗​−yi​))，它同样有所有的优点，而且比起hinge，塔处处可微。（特别是在xgboost 场景下，二阶可微就很重要了）

分位数损失 则是预测范围，而不是精确到点： L = ∑ i : y i < y i ∗ ( 1 − α ) ∣ y i − y i ∗ ∣ + ∑ i : y i > = y i ∗ α ∣ y i − y i ∗ ∣ L=\sum_{i:y_i=y_i^* } \alpha|y_i-y_i^*| L=i:yi​<yi∗​∑​(1−α)∣yi​−yi∗​∣+i:yi​>=yi∗​∑​α∣yi​−yi∗​∣,$\alpha$是分位数，主要根据对正误差和反误差的重视程度

最大似然MLE与最大后验MAP

• MLE是在各种概率中，找出使发生事实概率最大的那个概率。 θ M L E ( x ) = a r g m a x θ f ( x ∣ θ ) \theta_{MLE}(x)=arg max_{\theta} f(x|\theta) θMLE​(x)=argmaxθ​f(x∣θ)然后依据独立同分布展开式子求导为0即可求出参数。
• MAP是在各种概率中，找出使发生事实概率最大的那个概率+估计量的先验分布。 θ M A P = a r g m a x f ( θ ∣ x ) = a r g m a x θ f ( x ∣ θ ) g ( θ ) \theta_{MAP}=arg maxf(\theta|x)=arg max_{\theta} f(x|\theta)g(\theta) θMAP​=argmaxf(θ∣x)=argmaxθ​f(x∣θ)g(θ)但是虽然MAP估计是考虑先验的，随着数据量越来越多的时候，先验的重要性会下降，所以MAP会逐步逼近于MLE估计。
• 贝叶斯估计。 MLE、MAP和贝叶斯估计是参数估计的三大法宝，MLE就是普通的估计，而MAP会多加一个先验分布，本质上都是先假定参数未知但为某确定数值，找到使得样本的似然分布最大的参数。 f ( θ ∣ x ) = ∫ θ f ( y ∣ x , θ ) f ( θ ∣ x ) d θ f(\theta|x)=\int_{\theta}f(y|x,\theta)f(\theta|x) d\theta f(θ∣x)=∫θ​f(y∣x,θ)f(θ∣x)dθ而贝叶斯估计是把参数假定是服从某种先验概率分布的随机变量而不是确定数值，然后在样本分布上，计算参数所有的可能，并通过计算参数的期望，得到后验概率密度（可以理解为加权）。当贝叶斯估计复杂度变大的时候，可以使用MCMC进行近似。

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！