第一单元 用python学习微积分（四） 链式法则及高阶导数（上）- 通用公式的推导

本文内容来自学习麻省理工学院公开课：单变量微积分-链式法则及高阶导数-网易公开课

开发环境准备：CSDN

目录

一、公式推导

1、乘法法则 (uv)' = u'v + v'u

2、除法法则 ​

3、除法法则应用

一、公式推导

1、乘法法则 (uv)' = u'v + v'u

d(uv)'/dx =

(这里分子中凭空添加2项u(x)v(x+Δx) 一正一负)

(由于Δx =>0)

= vu' + u v'

这里讨论下， u' 实际是u(x)' 所以是u(x)的导数，所以vu' + uv'应该分别用python对u(x)和v(x)求导

举个栗子：

对z(x)求导： 根据公式 z(x)' = u(x)'v(x) + v(x)'u(x)，

在python中先后求得u(x)' 和v(x)'的导数

from sympy import *
x= symbols('x')
gfg_exp = x**2+5
dif = diff(gfg_exp, x)
dif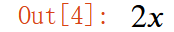     

from sympy import *
x= symbols('x')
gfg_exp = 1 / x**3
dif = diff(gfg_exp, x)
dif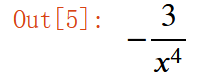

将结果带入： z(x)' = u(x)'v(x) + v(x)'u(x) = 2x * v(x) + -3/x**4 * u(x)

x, u, v = symbols('x u v')
expr = 2 * x * v + -3/x**4 * u
expr.subs(v,1/x**3).subs(u, x**2+5)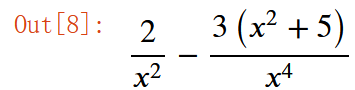

2、除法法则

当Δx趋近0

3、除法法则应用

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！