【Leetcode刷题篇】-Leetcode1334 阈值邻居内最少的城市

有 n 个城市，按从 0 到 n-1 编号。给你一个边数组 edges，其中 edges[i] = [fromi, toi, weighti] 代表 fromi 和 toi 两个城市之间的双向加权边，距离阈值是一个整数 distanceThreshold。

返回能通过某些路径到达其他城市数目最少、且路径距离 最大 为 distanceThreshold 的城市。如果有多个这样的城市，则返回编号最大的城市。

注意，连接城市 i 和 j 的路径的距离等于沿该路径的所有边的权重之和。

示例 1：

输入：n = 4, edges = [[0,1,3],[1,2,1],[1,3,4],[2,3,1]], distanceThreshold = 4
输出：3
解释：城市分布图如上。
每个城市阈值距离 distanceThreshold = 4 内的邻居城市分别是：
城市 0 -> [城市 1, 城市 2]
城市 1 -> [城市 0, 城市 2, 城市 3]
城市 2 -> [城市 0, 城市 1, 城市 3]
城市 3 -> [城市 1, 城市 2]
城市 0 和 3 在阈值距离 4 以内都有 2 个邻居城市，但是我们必须返回城市 3，因为它的编号最大。
示例 2：

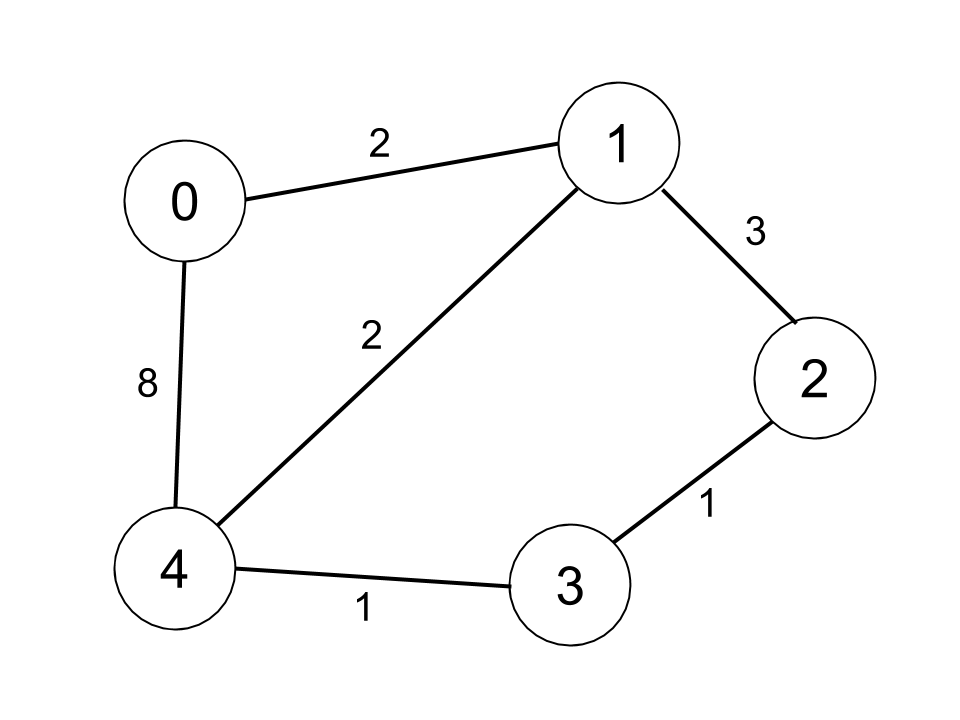
输入：n = 5, edges = [[0,1,2],[0,4,8],[1,2,3],[1,4,2],[2,3,1],[3,4,1]], distanceThreshold = 2
输出：0
解释：城市分布图如上。
每个城市阈值距离 distanceThreshold = 2 内的邻居城市分别是：
城市 0 -> [城市 1]
城市 1 -> [城市 0, 城市 4]
城市 2 -> [城市 3, 城市 4]
城市 3 -> [城市 2, 城市 4]
城市 4 -> [城市 1, 城市 2, 城市 3]
城市 0 在阈值距离 2 以内只有 1 个邻居城市。

class Solution {public int findTheCity(int n, int[][] edges, int distanceThreshold) {int[][] graph = new int[n][n];// 初始化for(int i=0;i<n;i++){for(int j=0;j<n;j++){if(i==j){graph[i][j] = 0;}else{graph[i][j] = Integer.MAX_VALUE;}}}//  初始化for(int[] edge:edges){graph[edge[0]][edge[1]] = graph[edge[1]][edge[0]] = edge[2];}// floydfor(int k=0;k<n;k++){for(int i=0;i<n;i++){for(int j=0;j<n;j++){if(i!=k&&j!=k&&graph[i][k]!=Integer.MAX_VALUE&&graph[k][j]!=Integer.MAX_VALUE){graph[i][j] = Math.min(graph[i][j],graph[i][k]+graph[k][j]);}}}}// get resint min = n + 1;int res = -1;for(int i=0;i<n;i++){int count = 0;for(int j=0;j<n;j++){if(i!=j&&graph[i][j]<=distanceThreshold){count++;}}if(min>=count){min = count;res = i;}}return res;}
}