世界的本质是旋转(2) 旋转叠加与傅里叶变换
转载: https://blog.csdn.net/goldenhawking/article/details/51352240
1.旋转的叠加
上一次,我们观察了单一余弦震动可以表示为两个等模共轭矢量的旋转运动叠加。其实,早在高中时,课本里就有波的叠加的概念。假设现在在复平面上有两个旋转分量,其在某个时刻的状态(姑且叫做0时刻吧)如下图所示: 
从数学上说,在t时刻,两对(共4个)矢量的加成为:
根据上一篇的欧拉公式,
s(t)=a1⋅cos(2πjf1t+θ1)+a2⋅cos(2πjf2t+θ2)s(t)=a1⋅cos(2πjf1t+θ1)+a2⋅cos(2πjf2t+θ2)
其中,
f1=300Hz,f2=500Hz,θ1=π6,θ2=34πf1=300Hz,f2=500Hz,θ1=π6,θ2=34π
a1=1,a2=0.45a1=1,a2=0.45
画出来是酱紫的:

t = 0:0.00025:1-0.00025;
f1=300;
f2=200;
theta1=pi/6;
theta2=pi*3/4;
s = cos (2*pi*f1* t + theta1) + 0.45*cos(2*pi*f2*t+theta2);
>> plot (t,s);- 1
- 2
- 3
- 4
- 5
- 6
- 7
当然了,我们可以任意安排成对的共轭旋转,获得千奇百怪的图案,比如这个由6组幅度、起始角度、转速(频率)组成的运动:
t = 0:0.00025:1-0.00025;a = [7,1300,7,7,535,7];f = [ 5 ,501,997, 1005,1501, 1997]';theta =[-1.4182,-1.1831,1.4182,-1.4182,-0.3977,1.4182]'; s = a * cos(2 * pi * f * t + theta * ones(1,4000)); plot(t,s)- 1
- 2
- 3
- 4
- 5
- 6
已经和余弦不太像了吧!
如果我们找到几千组呢?
可以想象,使用N多组旋转,就可以组合出任意的形状来。
太好了!搜索互联网,发现在这篇博文中,已经把它说的非常清楚啦!不过要说明的是,下面动画中合成的并不是实信号,而是取的虚半轴投影。
“知乎专栏”
看看方波的合成: 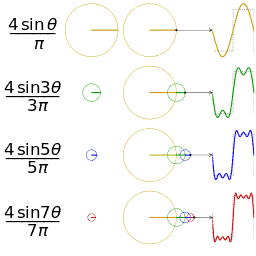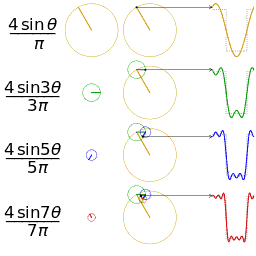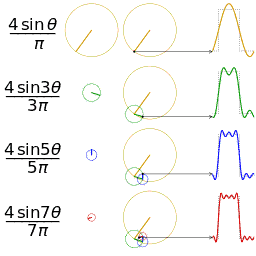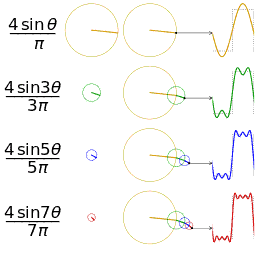
看看三角波: 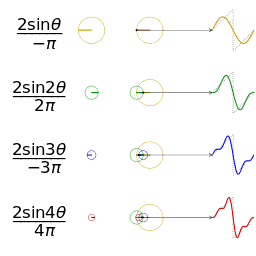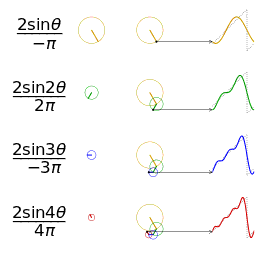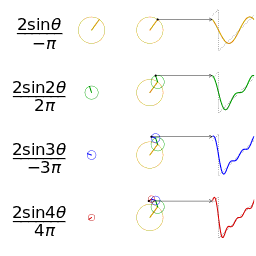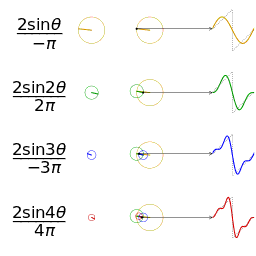
上面的图片是维基百科的哦!
2.傅里叶变换
上面的概念如果反过来,给定一个波形,我如何构造一组旋转,可以恰好使我们的复平面叠加点上的小钢笔画出同样的形状呢?显然我们需要知道每个旋转的转速(频率)、棍子长度(幅度)和起始0时刻的角度(相位)。
2.1 解旋转与均值
傅里叶变换是解决这个问题的工具,他的核心理念很简单。想知道这个波形是否含有某个频率f的旋转?? 那就按照f 反着转,看看有没有棍子保持不动吧!先看两个图,
a: 频率为f的旋转以-f解旋转,先向前转了几度,再向后倒退了相同度数,因此无论何时观察,都保持不动.
图中,红色为t时刻的棍子,绿色为 t+时刻其应该在的位置;但是,由于我们施加了一个和f相反的旋转-f,结果t+时刻棍子被转回去了(蓝色)。 
如果我们不断的对这个图片拍照,该棍子永远停留在相同的位置。如果对这个位置的坐标求重心(均值),则其与上图位置重合。
b: 频率不等于f的旋转以-f解旋转,尽管又叠加了f,但仍旧为旋转状态,各个时刻位置不断变化 
如果我们对它拍照,底片是这样的 
如果对它求均值或者求和,恒为0.
2.2 施加旋转的数学描述
在复平面上,把一个矢量αα旋转一个角度θθ ,旋转后的矢量α′α′为:
对应到2.1节的需求,对任一个时刻t, 波形s(t)按照给定频率-f旋转后的新波形
s′(t)=s(t)⋅e2π(−f)t⋅j=s(t)⋅e−2πjfts′(t)=s(t)⋅e2π(−f)t⋅j=s(t)⋅e−2πjft
2.3求和/求均值的数学描述
求和在数学上是进行积分
S(f)=∫∞−∞s′(t)dt=∫∞−∞s(t)⋅e−2πjftdtS(f)=∫−∞∞s′(t)dt=∫−∞∞s(t)⋅e−2πjftdt这正是傅里叶变换的基本公式。
# sjf
3What’s the next?
太多问题啦!详见下一章(世界的本质是旋转3-拍照与采样 )
为什么实信号的傅里叶变换是对称的?
课本里模拟波形的采样,也就是 A/D,怎么好好理解呢?
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!

