State Estimation and Localization for Self-Driving Cars-W1_最小二乘法估计电阻
State Estimation and Localization for Self-Driving Cars-W1_最小二乘法估计电阻
- 最小二乘法
- 练习
- 介绍
- 开始
- 估计斜率参数
- 绘制结果
最小二乘法
来到Coursera自动驾驶系列课程第二部分《State Estimation and Localization for Self-Driving Cars》,介绍一个简单的利用最小二乘来估计电阻的例子,假设对电阻做了四次测量,分别得到四个电阻值,那么如何估计出真实的电阻值。

假设x是一个未知的常数,y表示电阻的测量值,建立测量模型为:
y=x+v
其中,v表示测量噪声。
将公式对应到四个测量值:

计算出每次测量误差的平方e12、e22。电阻的“最佳”估计是最小化平方误差总和的估计。

让我们使用向量重写上式:
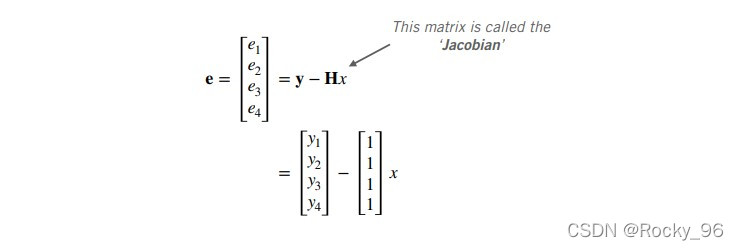
现在,我们可以将标准表达如下,

为了最小化这个公式,我们可以计算关于x的偏导数,将结果设置为 0,并求解一个极值:

只有当 ( H T H ) − 1 ) \mathbf{(HTH)^-1^ )} (HTH)−1)存在时可以得到x值。
分享:科罗拉多大学 PhET 交互式模拟项目提供的交互式最小二乘拟合模拟器:https://phet.colorado.edu/sims/html/least-squares-regression/latest/least-squares-regression_en.html
以下是课程中配套的程序练习:
练习
介绍
使用欧姆定律确定电气组件的电阻。 电阻的计算公式:
V = R I V = RI V=RI
其中 V V V 是以伏特为单位的电压, R R R 是以欧姆为单位的电阻,而 I I I 是以安培为单位的电流。 使用万用表测量不同电流值下电阻器上的压降并收集以下数据:
| 电流(A) | 电压(V) |
|---|---|
| 0.2 | 1.23 |
| 0.3 | 1.38 |
| 0.4 | 2.06 |
| 0.5 | 2.47 |
| 0.6 | 3.17 |
有了手头的数据,目标是:
- 使用最小二乘法将一条穿过原点的线(即,确定 y = R x y = Rx y=Rx 的参数 R R R)与该数据拟合。 您可以假设所有测量都具有同等精度。
- 考虑该组件的最佳电阻估计值(以欧姆为单位)。
开始
第一步是导入必要的 Python 模块并将电流值和电压测量值加载到 NumPy 数组中:
import numpy as np
from numpy.linalg import inv
import matplotlib.pyplot as plt# Store the voltage and current data as column vectors.
I = np.array([[0.2, 0.3, 0.4, 0.5, 0.6]]).T
V = np.array([[1.23, 1.38, 2.06, 2.47, 3.17]]).T
绘制测量值,看到电流和电压之间基本呈现线性关系。
plt.scatter(I, V)
plt.xlabel('Current (A)')
plt.ylabel('Voltage (V)')
plt.grid(True)
plt.show()

估计斜率参数
让我们使用上边推导出的最小二乘公式来估计斜率参数 R R R(即电阻):

寻找斜率参数 R R R,如何定义矩阵 H \mathbf{H} H(雅可比矩阵)和向量 y \mathbf{y} y(包含堆叠电压测量值) ? 提示 1:在复习模块 1 的材料时,请仔细注意欧姆定律定义的关系(这个问题与模块中提供的示例略有不同)。 提示2:雅可比矩阵包含测量方程关于感兴趣参数的偏导数。
# Define the H matrix - what does it contain?
# H = ...
H=I.reshape(I.shape[0],1)
y=V.reshape(V.shape[0],1)
R=np.linalg.inv(H.T@H)@(H.T@y)
print('The slope parameter of the best-fit line (i.e., the resistance) is:')
print(R[0, 0])
The slope parameter of the best-fit line (i.e., the resistance) is:
5.13444444
绘制结果
现在让我们结果。 如何将线性参数拟合与以欧姆为单位的电阻值相关联?
I_line = np.arange(0, 0.8, 0.1).reshape(8, 1)
V_line = R*I_lineplt.scatter(I, V)
plt.plot(I_line, V_line)
plt.xlabel('Current (A)')
plt.ylabel('Voltage (V)')
plt.grid(True)
plt.show()

如果您正确地实施了这些步骤,斜率参数 R ^ \hat{R} R^ 应该非常接近(在十分之几欧姆内) R = 5 Ω R = 5~\Omega R=5 Ω 的实际电阻值。 然而,估计值不会与真实电阻值完全匹配,因为我们只有有限数量的噪声测量。
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!