HashMap源码(JDK1.8)深度分析-红黑树(插入)
阅读本专栏需要了解HashMap底层数组+链表+红黑树的数据结构。红黑树的源码比较复杂,分插入和删除两期来讲,本文只说插入。文章很长,需要花一些精力仔细阅读。文章内容是本人阅读HashMap源码结合查阅资料形成,如有不对的地方,欢迎留言讨论,确实有误的我会及时更正。
红黑树时一种二叉查找树,不是平衡二叉树,这些概念不了解的,建议先去了解一下。在二叉查找树的基础上,红黑树又有以下五个性质:
性质1. 结点是红色或黑色。
性质2. 根结点是黑色。
性质3. 所有叶子都是黑色。(叶子是NIL结点)
性质4. 每个红色结点的两个子结点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色结点)
性质5. 从任一节结点到其每个叶子的所有路径都包含相同数目的黑色结点。
HashMap的putVal方法中,会判断根据Hash值计算出的数组下标对应的元素是否是红黑树节点(详见本专栏的另一盘文章《HashMap源码(JDK1.8)分析-putVal》),如果是树节点,则调用树节点的putTreeVal。我们先从putTreeVal开始分析,然后再把链表的树化说一下,最后再说插入自平衡方法balanceInsertion。
本文目录如下:
目录
putTreeVal红黑树版本的putVal方法
tieBreakOrder最终裁决
moveRootToFront将根节点移动到链表头部
treeifyBin尝试链表树化
treeify链表树化
balanceInsertion插入自平衡
再看一遍红黑树的性质
插入操作带来的红黑数变化的所有情形
红黑树平衡的旋转操作
左旋rotateLeft
右旋rotateRight
各种情形的解决办法
情形1:插入的节点是根节点
情形2:插入节点的父节点是黑节点
情形3.1和3.3:插入节点的父节点是红节点,叔叔节点也是红节点
情形3.2和3.4:当前节点的父节点为红节点,叔叔节点为空或叔叔节点是黑节点
balanceInsertion源码
putTreeVal红黑树版本的putVal方法
该方法开始先从根节点对树进行查找,查找的方法如下:
1、先通过hash值判断,应该继续在左子树还是右子树查找
2、找到hash值相同的子树后,先看子树的根节点是否是要找的key
3、如果不是,看能够通过compareto的方式继续判断应该在左子树继续查找,还是右子树继续查找(dir的值)
3.1、 判断不出来,则分别调用左右子树的find方法,看能否找到
3.1.1、找到了直接返回该节点
3.1.2、找不到,说明就是没有了
3.2、调用tieBreakOrder(k, pk)计算应该将该节点放到左子树还是右子树(dir的值)
判断结束后,通过dir的值,看左节点或有节点是否为空,为空则直接挂上,
不为空,则p指向相应的左节点或有节点,再次循环查找
//((TreeNode)p).putTreeVal(this, tab, hash, key, value);//查找的思路:// 先通过hash值判断,应该继续在左子树还是右子树查找// 找到hash值相同的子树后,先看子树的根节点是否是要找的key// 如果不是,看能够通过compareto的方式继续判断应该在左子树继续查找,还是右子树继续查找(dir的值)// 判断不出来,则分别调用左右子树的find方法,看能否找到,找到了直接返回// 找不到,说明就是没有了,此时要调用tieBreakOrder(k, pk)计算应该将该节点放到左子树还是右子树(dir的值)// 判断结束后,通过dir的值,看左节点或有节点是否为空,为空则直接挂上,// 不为空,则p指向相应的左节点或有节点,再次循环查找final TreeNode putTreeVal(HashMap map, Node[] tab,int h, K k, V v) {Class kc = null;boolean searched = false;//取根节点TreeNode root = (parent != null) ? root() : this;//从根节点开始查找for (TreeNode p = root;;) {int dir, ph; K pk;/*整个循环体可以看做是两块判断第一块判断是第一个if和下面的三个elseif,用来查找当前key和计算dir的值第二块是根据计算好的dir的值判断当前节点应该挂在p上,还是继续循环查找*///先比较Hash值,计算dirif ((ph = p.hash) > h)dir = -1;else if (ph < h)dir = 1;//算不出来,则看当前节点是否是要找的节点,是的话直接返回else if ((pk = p.key) == k || (k != null && k.equals(pk)))return p;//走到这里说明当前节点肯定不是要查找的节点//此时通过compareto的方式计算应该在左子树继续查找,还是右子树继续查找,//此时还找不到,说明就是找不到了。//接着,通过tieBreakOrder计算应该将该节点挂在左子树还是右子树else if ((kc == null &&(kc = comparableClassFor(k)) == null) ||(dir = compareComparables(kc, k, pk)) == 0) {//如果算不出来(compareComparables(kc, k, pk)) == 0),且尚未在左子树或右子树查找过,则分别遍历左子树或右子树,看能否找到。//如果已经遍历过了(searched = true),则直接走到tieBreakOrder计算最终的dirif (!searched) {TreeNode q, ch;searched = true;if (((ch = p.left) != null &&(q = ch.find(h, k, kc)) != null) ||((ch = p.right) != null &&(q = ch.find(h, k, kc)) != null))//找到了直接返回,找不到还是走到tieBreakOrder计算最终的dir,此时则认为树中没有key值return q;}dir = tieBreakOrder(k, pk);}TreeNode xp = p;//根据计算好的dir,看应该指向左子树还是右子树//如果指向的子树为空则进入if代码块直接将节点挂上if ((p = (dir <= 0) ? p.left : p.right) == null) {Node xpn = xp.next;//根据k,v,hash创建TreeNodeTreeNode x = map.newTreeNode(h, k, v, xpn);//看应该挂在左节点还是右节点if (dir <= 0)xp.left = x;elsexp.right = x;//维护好双向链表的结构,该节点放在了其父节点的后面xp.next = x;x.parent = x.prev = xp;if (xpn != null)((TreeNode)xpn).prev = x;//调用插入自平衡方法和移动根节点到链表头的方法moveRootToFront(tab, balanceInsertion(root, x));return null;}}} putTreeVal调用了tieBreakOrder、moveRootToFront、balanceInsertion三个方法,我们接着看。
tieBreakOrder最终裁决
这个方法没有什么可说的,就是强制调用了Object.hashCode()方法去计算dir,不管key本身有没有重写hashCode(),都会直接去调用原始的hashCode方法,注意即便这样也有可能两个key的HashCode是重复的。
//最终裁决方法static int tieBreakOrder(Object a, Object b) {int d;//a\b都不为nullif (a == null || b == null ||//先比较a,b的类名字符串,看返回值是不是0(d = a.getClass().getName().compareTo(b.getClass().getName())) == 0)//仍然返回0的话,调用System.identityHashCode去比较//System.identityHashCode会强制调用Object.hashCode()//a<=b返回-1,a>b返回1d = (System.identityHashCode(a) <= System.identityHashCode(b) ?-1 : 1);return d;}moveRootToFront将根节点移动到链表头部
这个方法是将树结构的root节点移动到双向链表的头部,HashMap在将链表进行树化的时候,并没有丢失链表结构,反而强化成了双向量表。在调用插入自平衡方法时,树结构的根节点可能会随着节点的旋转发生变化,该方法保证根节点永远在链表的头部。注意,它是TreeNode的一个方法。
static void moveRootToFront(Node[] tab, TreeNode root) {int n;//一些合法性校验if (root != null && tab != null && (n = tab.length) > 0) {//计算根节点的下标int index = (n - 1) & root.hash;//取到链表的头结点,即为table[index]位置的节点TreeNode first = (TreeNode)tab[index];if (root != first) {//根节点不是头结点,则开始调整//声明一个变量为根节点的next节点,可能为nullNode rn;//tab[index]赋值为根节点tab[index] = root;//根节点的prev节点TreeNode rp = root.prev;//根节点的next节点不为空if ((rn = root.next) != null)//根节点的next节点的prev指向各节点的prev((TreeNode)rn).prev = rp;//根节点的prev不为空if (rp != null)//根节点的prev节点的next节点指向根节点的next节点rp.next = rn;//如果原头结点不为空if (first != null)//原头结点的prev节点指向rootfirst.prev = root;//根节点的next指向原头节点root.next = first;//根节点的prev节点置为空root.prev = null;}//校验红黑树的正确性,使用断言的方式//断言默认是不生效的,如果要生效需要更改jvm的-ea参数//断言生效的情况下,如果下面的函数返回false,说明红黑树的正确性出现了问题,系统会强制报错//断言不生效,则此处只是个校验,不会有什么提示assert checkInvariants(root);}}
接下来我们先把树化方法讲一下,树化方法也调用了插入自平衡,讲完树化方法后,再重点说插入自平衡方法。
treeifyBin尝试链表树化
这个方法用来将tab的某个元素进行树化,它有两个入参Node
//将链表进行树化final void treeifyBin(Node[] tab, int hash) {int n, index; Node e;//判断数组长度是否超过了树化阈值MIN_TREEIFY_CAPACITY(64)//不超过64的话,优先对数组进行扩容//原因是:数组较短的话,后续扩容的可能性很大,而红黑树的扩容比较耗费性能// 因此先走扩容,避免树化后,后续频繁对树进行扩容。// 另外,作者还是希望数组尽可能长,让节点尽可能散列在数组的元素上,// 充分发挥出散列查找时间复杂度O(1)的优势。// 从数组的扩容机制就可以看出,数组扩容阈值的判断,不是数组占用量达到了阈值,// 而是节点总数达到了阈值,不管这些节点在链表还是红黑树中。// 极端情况下,所有的节点都集中在一颗红黑树上,也会触发扩容机制。if (tab == null || (n = tab.length) < MIN_TREEIFY_CAPACITY)//调用扩容方法resize();//如果已经达到了树化阈值,则开始进行树化else if ((e = tab[index = (n - 1) & hash]) != null) {//声明两个变量用来存储头结点和尾结点TreeNode hd = null, tl = null;do {//将节点转换为树节点,就是创建一个树节点,并返回/*TreeNode replacementTreeNode(Node p, Node next) {return new TreeNode<>(p.hash, p.key, p.value, next);}*/TreeNode p = replacementTreeNode(e, null);//这一段代码是创建双向链表结构if (tl == null)hd = p;else {p.prev = tl;tl.next = p;}tl = p;//循环遍历} while ((e = e.next) != null);//重新赋值table[index],并判断是否为nullif ((tab[index] = hd) != null)//开始树化hd.treeify(tab);}} treeify链表树化
接着又调用了treeify方法,这个方法是Node节点的方法,由头结点来调用。相当于从头结点开始遍历,将每个节点转换为树节点后,插入到红黑树,并做插入自平衡。
//以头节点为根节点,对链表进行树化final void treeify(Node[] tab) {//声明一个变量保存根节点TreeNode root = null;//for循环,从头结点开始遍历链表for (TreeNode x = this, next; x != null; x = next) {next = (TreeNode)x.next;//当前节点的做孩子和右孩子置为空x.left = x.right = null;//如果根节点为空,把当前节点设置为根节点//第一次你进入循环会执行该代码if (root == null) {x.parent = null;//根节点为黑节点(红黑树的性质约定)x.red = false;root = x;}else {//否则开始计算当前节点在红黑树的位置K k = x.key;int h = x.hash;Class kc = null;//for循环从根节点开始查找for (TreeNode p = root;;) {int dir, ph;K pk = p.key;//前面两个判断条件试图从hash值判断出,当前节点应该在该树节点的左子树还是右子树if ((ph = p.hash) > h)//h 小于该树节点的 hash值,则dir = - 1,意味着当前节点在该树节点的左子树dir = -1;else if (ph < h)//反之则是右子树dir = 1;//如果两个key的hash值相同(这并不少见)//检验两个对象是否具有比较资格//(kc == null && (kc = comparableClassFor(k)) == null) 这一句用来判断k的类是否实现了Comparable接口,//如果是,再执行第三个条件dir = compareComparables(kc, k, pk)) == 0,比较两个key调用compareTo的结果是不是0//不是0的话,不再进入else if,直接使用返回值//如果是0则意味着没比较出大小,此时调用tieBreakOrder做最终裁决else if ((kc == null &&(kc = comparableClassFor(k)) == null) ||(dir = compareComparables(kc, k, pk)) == 0)//最终裁决dir = tieBreakOrder(k, pk);TreeNode xp = p;//根据算出的dir来判断应该在p的左子树还是右子树继续查找。//如果要查找的子树根节点为null,则把节点挂在该处if ((p = (dir <= 0) ? p.left : p.right) == null) {//执行x的父节点为xp(即为刚才的p节点)x.parent = xp;//根据dir制定挂在xp的左孩子还是右孩子if (dir <= 0)xp.left = x;elsexp.right = x;//调用平衡树方法balanceInsertion,这个方法是插入时用来平衡红黑树的//根节点可能会随着平衡改变,因此返回新的根节点root = balanceInsertion(root, x);break;}}}}//根节点发生变化后,可能就不再是链表的头结点了//此时把根节点移动到链表的头部moveRootToFront(tab, root);} 好了,下面重点说一下最复杂的插入自平衡方法。
balanceInsertion插入自平衡
本节建议结合这红黑树插入自平衡方法balanceInsertion(文末)的源码来看。
再看一遍红黑树的性质
红黑树是一种二叉查找树(非平衡二叉树),在二叉查找树的基础上,又有以下5个性质。
性质1. 结点是红色或黑色。
性质2. 根结点是黑色。
性质3. 所有叶子都是黑色。(叶子是nil结点)
性质4. 每个红色结点的两个子结点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色结点)
性质5. 从任一节结点到其每个叶子的所有路径都包含相同数目的黑色结点。
注意:新插入的节点均为红节点,目的尽量不改变红黑树的性质5。
几个要用到的名字解释
nil节点:红黑树每个叶子节点的虚拟子节点(这也就是说为什么性质3说所有的叶子节点都是黑色nil节点),HashMap的红黑树源码并未有任何nil节点的操作,这里的nil节点帮助大家理解红黑树的属性和变换方法。
黑高:某一个树节点到其所有叶子节点的黑色节点的个数,nil节点的黑高为0。
插入操作带来的红黑数变化的所有情形
分为以下情形来处理(用x节点代表插入节点):
1.插入节点x是根节点,则直接将节点变为黑节点。满足性质2。
2.插入节点x的父节点为黑节点,不做任何操作,直接返回,因为没有破坏红黑树的任何性质。
3.插入节点x的父节点为红节点,此时又分几种情况:
3.1.x节点的父节点是x节点祖父节点的左孩子,且x节点的右叔叔节点为红节点
此时需要将x节点的父节点变色为黑节点,x的右叔叔节点变为黑节点,x节点的祖父节点变为红节点,并以x节点的祖父节点为当前节点,继续循环向上判断是否还满足红黑树的原则。
3.2.x节点的父节点是x节点祖父节点的左孩子,且x节点的右叔叔节点为黑节点(或为空,空节点也是黑节点)
此时再判断x是其父节点的左孩子还是右孩子
3.2.1.如果是右孩子,则对x节点的父节点执行左旋操作,左旋后x的父节点成为x的左孩子,符合3.2.2的情形,再执行3.2.2
3.2.2.如果是左孩子,则x的父节点变色为黑节点,x的祖父节点变色为红节点,并将x的祖父节点进行右旋
3.3.x节点的父节点是x节点祖父节点的右孩子,x节点的左叔叔为红节点
此时需要将x节点的父节点变为黑节点,x节点的左叔叔变为黑节点,x节点的祖父节点变为红节点,并以x节点的祖父节点为当前节点,继续循环向上判断是否还满足红黑树的原则。
3.4.x节点的父节点是x节点祖父节点的右孩子,x节点的左叔叔为黑节点(或为空)
仍然分两种情况,判断x节点是左孩子还是右孩子
3.4.1.如果x节点是左孩子,则将x节点的父节点进行右旋,右旋后x的父节点为x的右孩子,符合3.4.2的情形,再按3.4.2执行
3.4.2.如果x节点是右孩子,则将x节点的父节点变为黑节点,x节点的祖父节点变为红节点,然后对x节点的祖父节点进行左旋
红黑树平衡的旋转操作
分为左旋和右旋,不只是红黑树,二叉查找树和二叉平衡树,也是左旋和右旋两个操作。先看一下左旋和右旋两个基本操作,然后讲一下,为什么这样操作后就可以保证红黑树的性质。
左旋rotateLeft
旋转接点为p节点
p节点成为p节点的右孩子的左孩子,p节点的右孩子成为其父节点
p节点右孩子的左孩子成为p节点的右孩子
p节点若为根节点,则旋转后新的根节点为p节点的右孩子
如下图:
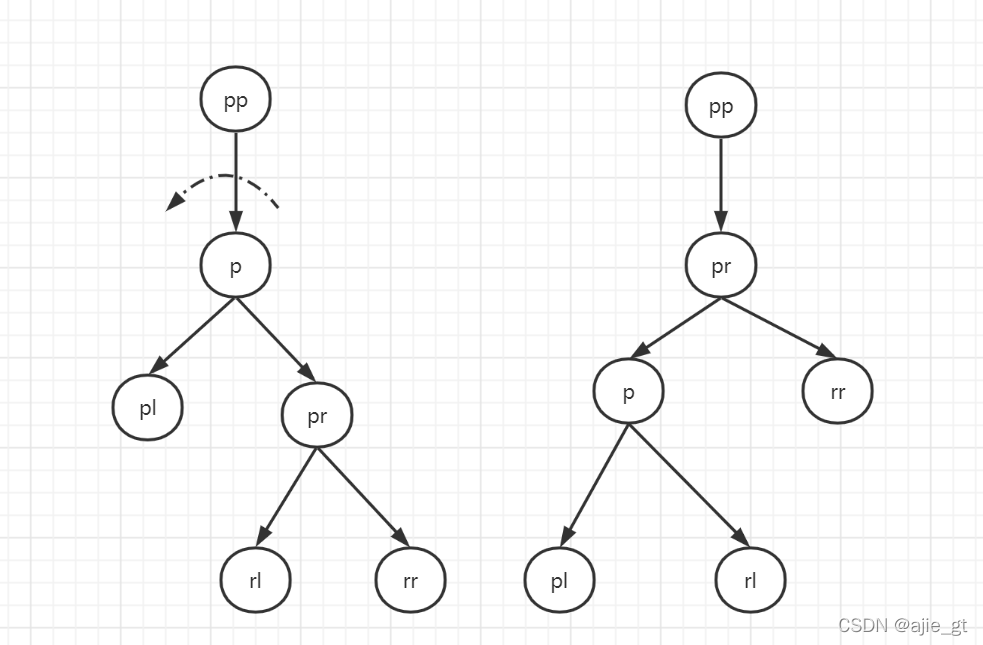
代码如下:
//将p节点左旋//p节点成为p节点的右孩子的左孩子,p节点的右孩子成为其父节点//p节点右孩子的左孩子成为p节点的右孩子//p节点若为根节点,则旋转后新的根节点为p节点的右孩子,注意变色和更新rootstatic TreeNode rotateLeft(TreeNode root,TreeNode p) {TreeNode r, pp, rl;if (p != null && (r = p.right) != null) {if ((rl = p.right = r.left) != null)rl.parent = p;if ((pp = r.parent = p.parent) == null)(root = r).red = false;else if (pp.left == p)pp.left = r;elsepp.right = r;r.left = p;p.parent = r;}return root;} 右旋rotateRight
旋转节点为p节点
p节点的左孩子成为p节点的父节点,p节点成为其左孩子的右孩子
p节点左孩子的右孩子成为p节点的左孩子
p节点若为根节点,则旋转后新的根节点为p节点的左孩子
如下图:
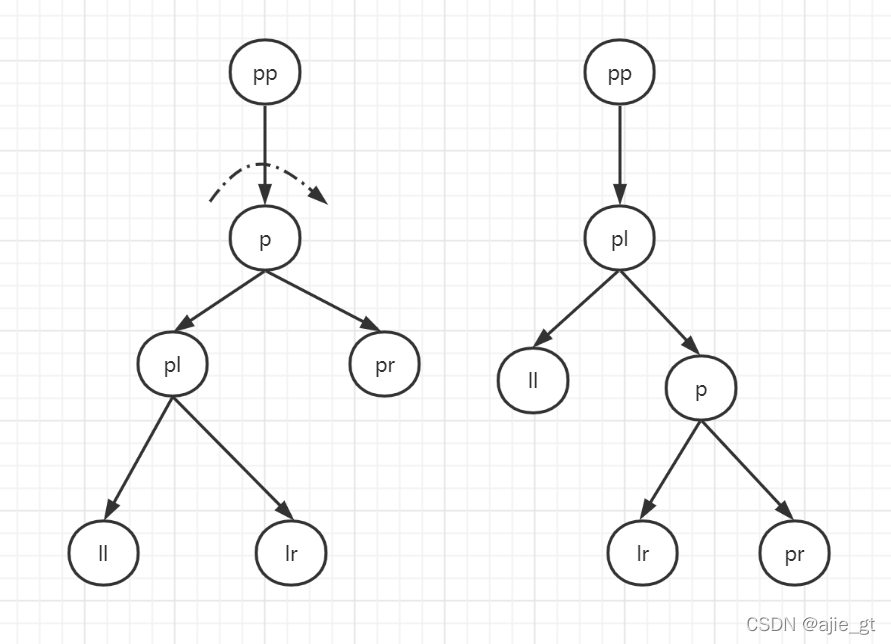
代码如下:
//将p节点右旋//p节点的左孩子成为p节点的父节点,p节点成为其左孩子的右孩子//p节点左孩子的右孩子成为p节点的左孩子//p节点若为根节点,则旋转后新的根节点为p节点的左孩子,注意变色和更新rootstatic TreeNode rotateRight(TreeNode root,TreeNode p) {TreeNode l, pp, lr;if (p != null && (l = p.left) != null) {if ((lr = p.left = l.right) != null)lr.parent = p;if ((pp = l.parent = p.parent) == null)(root = l).red = false;else if (pp.right == p)pp.right = l;elsepp.left = l;l.right = p;p.parent = l;}return root;} 各种情形的解决办法
通过图示解释一下各种情形的解决办法,以及为什么这样能保证红黑树的性质。
首先一个大前提是,我们在插入节点之前,hashMap的树结构是严格的红黑树结构,插入节点后,基于原来这个严格的红黑树进行以下处理就能保证自平衡后仍然是一个严格的红黑树。为保证尽量不破坏红黑树的规则,默认插入的节点都是红节点。
x:当前节点,xp:当前节点的父节点,xpp:当前节点的祖父节点,xppr:当前节点的右叔叔节点(对3.3和3.4来说就是xppl:当前节点的左叔叔节点)
情形1:插入的节点是根节点
balanceInsertion源码L37
这没什么可说的,就一个节点,把它变成黑节点即可。
情形2:插入节点的父节点是黑节点
balanceInsertion源码L44
这种情况直接插入并不会破坏任何红黑树的属性,所以不用做任何处理。
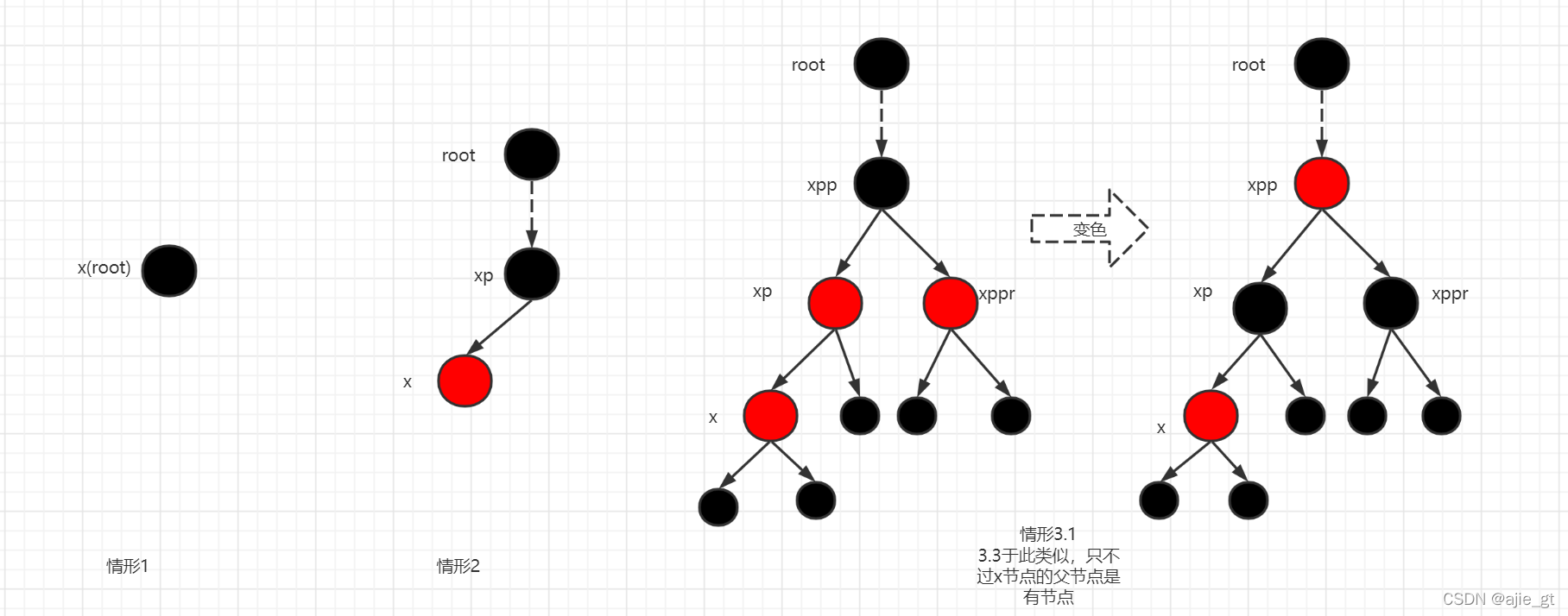
情形3.1和3.3:插入节点的父节点是红节点,叔叔节点也是红节点
balanceInsertion源码L49和L92
此时可以肯定祖父节点一定是黑节点(性质4保证),因此可以通过将父节点和叔叔节点变为黑节点,祖父节点变为红节点来保证以这个祖父节点为根节点的子树黑高不变。然后再以祖父节点为当前节点,继续向上判断是否破坏了其他树的红黑树性质,并继续循环处理,直到满足红黑树的性质。(小的黑节点是nil节点,在红黑树中不实际存在,为虚拟节点,黑高为0)
情形3.2和3.4:当前节点的父节点为红节点,叔叔节点为空或叔叔节点是黑节点
balanceInsertion源码L68-L88和L98-L111
为什么这里是当前节点而不叫插入节点,看后面“叔叔节点有可能为空(nil节点)或者一个实际存在的黑节点”。自平衡代码中通过一个无限循环体来判断各种情形,对于调整后可能不满足红黑树性质的情况,会继续执行下一次循环进行判断和处理。如果当前节点为新插入节点,则代表叔叔节点必然为空(nil节点);如果当前节点不是新插入节点(不是新插入节点的情况为上面情形3.1或3.3将插入节点的祖父节点变为红色,并将祖父节点作为当前节点继续向上判断是否破坏红黑树性质的情况,至少是第二次执行循环体),则叔叔节点必然是一个实际存在的黑节点(而且不是叶子节点)。
当前节点为新插入节点的情况
balanceInsertion源码L68和L98,叔叔节点为null的情况
如果当前节点x是新插入的节点,则这种情况下叔叔节点肯定是空节点。
下面论证一下这个论点:
假设此时右叔叔不为空,其黑高为n,则x的父节点的黑高必须为n,且n>=1(性质5决定)
由于x的父节点为一个红节点,因此x的父节点必须存在两个黑高为n的子树
显然这是不可能的,因为在x节点插入之前x的父节点必然存在一个Nil节点(黑高为0)。
下面以当前节点为插入节点(叔叔节点为nil节点)来说明,
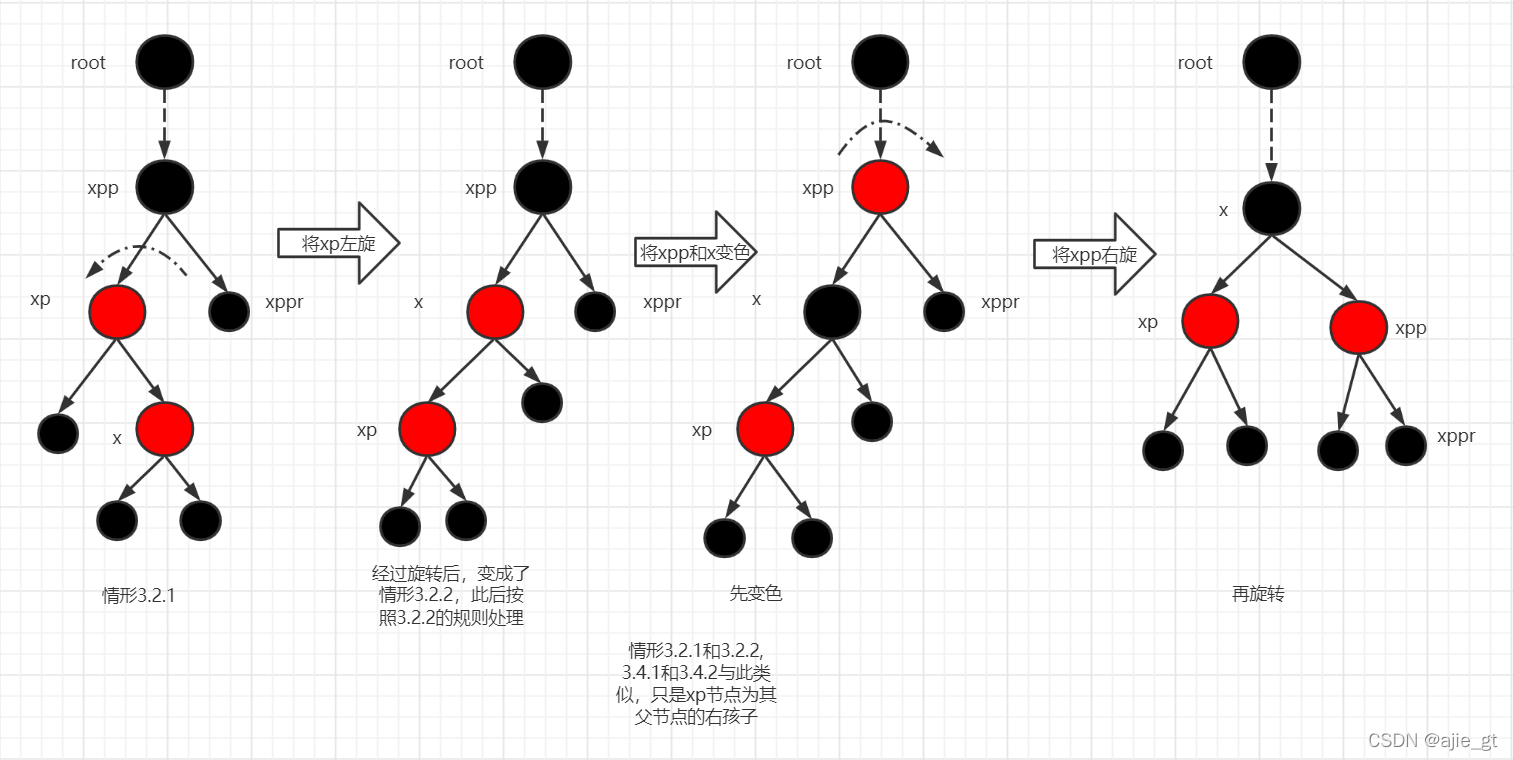
3.2和3.4是两种左右对称的情形,以3.2为例
3.2.1插入节点x节点为其父节点的右孩子节点,3.2.2插入节点x为其父节点的左孩子节点。
第一步:将xp节点左旋,变成3.2.2的情形,在按照3.2.2的情况来处理。
第二步:将x节点变为黑节点,将xpp节点变为红节点。
第三步:将xpp节点右旋。
可以看到,经过上面一顿操作后,xpp所在的子树黑高没有任何变化(保证了性质5),且没有两个连续的红节点(保证了性质4),整个操作没有对性质1、2、3有任何影响,因此仍然是严格的红黑树。
当前节点不是新插入节点的情况
balanceInsertion源码L68和L98,叔叔节点不为null且为黑节点的情况
如果当前节点不是插入节点,则只有可能是情形3.1经过操作后,祖父节点变为红节点并继续循环判断的情况(见下面的插入自平衡方法balanceInsertion源码L55)。这种情况当前x节点的叔叔节点肯定不是nil节点(红黑树的性质保证),其处理方法同上面是一样的,这里证明一下为什么这样处理不会破坏红黑树的性质5(很明显,上面已经证明了不会破坏红黑树的性质4)。
xpllt:x节点兄弟节点的左子树,xplrt:x节点兄弟节点的右子树:xlt:x节点的左子树,xrt:x节点的右子树,xpprlt:x节点叔叔节点的左子树,xpprrt:x节点叔叔节点的右子树。(x:当前节点,p:parent,l:left,r:right,t:tree(子树))
假设xpp处的黑高为n,根据红黑树的性质,
∴xp处的黑高为n-1,xppr处的黑高为n-1。
∵xp是红节点,
∴ xpl处的黑高为n-1,x处的黑高为n-1。
∵xppr为黑节点,xppr处的黑高为n-1
∴xpprlt的黑高为n-2,同样xpprrt的黑高为n-2
∵xpl为黑节点,xpl处的黑高为n-1
∴xpllt的黑高为n-2,同样xplr的黑高为n-2
∵x为红节点,x处的黑高为n-1
∴xlt处的黑高为n-1,xrt处的黑高为n-1
我们用f(x)来代表x节点处的黑高,则f(xpp) = n,f(xp) = f(xppr) = n-1, f(xpl) = f(x) = n-1,f(xpprlt) = f(xpprrt)=n-2,f(xpllt)=f(xplrt) = n-2,f(xlt) = f(xrt) = n-1。
因为下面6棵子树没有任何变化,所以其黑高是不变的,经过变换后(最右面的图):
f(xp) = f(xpl) = f(xpllt) + 1 = f(xplrt) + 1 = (n-2) + 1 = n - 1 = f(xlt)
f(xpp)= f(xppr) = f(xpprlt) + 1 = f(xpprrt) + 1 = (n-2) + 1 = n - 1 = f(xrt)
f(x) = f(xp) + 1 = f(xpp) + 1 = (n-1) + 1 = n
因此整个子树的黑高没有任何变化,可以证明,变换操作保证了红黑树的性质5。

balanceInsertion源码
//红黑树的插入自平衡方法/*红黑树是一种二叉查找树(非平衡二叉树),在二叉查找树的基础上,又有以下5个性质。性质1. 结点是红色或黑色。 性质2. 根结点是黑色。 性质3. 所有叶子都是黑色。(叶子是NIL结点) 性质4. 每个红色结点的两个子结点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色结点)性质5. 从任一节结点到其每个叶子的所有路径都包含相同数目的黑色结点。*///注意:新插入的节点均为红节点,目的尽量不改变红黑树的性质5//分为以下情况来处理//1:插入的节点是根节点,则直接将节点变为黑节点。满足性质2。//2:插入节点的父节点为黑节点,不做任何操作,直接返回,因为没有破坏红黑树的任何性质。//3:插入节点的父节点为红节点,此时又分几种情况:// 3.1:x节点的父节点是x节点祖父节点的左孩子,且x节点的右叔叔节点为红节点// 此时需要将x节点的父节点变色为黑节点,x的右叔叔节点变为黑节点,x节点的祖父节点变为红节点,并以x节点的祖父节点为当前节点,继续循环向上判断是否还满足红黑树的性质。// 3.2:x节点的父节点是x节点祖父节点的左孩子,且x节点的右叔叔节点为黑节点(或为空,空节点也是黑节点)// 此时再判断x是其父节点的左孩子还是右孩子// 3.2.1如果是右孩子,则对x节点的父节点执行左旋操作,左旋后x的父节点成为x的左孩子,符合3.2.2的情形,再执行3.2.2// 3.2.2如果是左孩子,则x的父节点变色为黑节点,x的祖父节点变色为红节点,并将x的祖父节点进行右旋// 3.3:x节点的父节点是x节点祖父节点的右孩子,x节点的左叔叔为红节点// 此时需要将x节点的父节点变为黑节点,x节点的左叔叔变为黑节点,x节点的祖父节点变为红节点,并以x节点的祖父节点为当前节点,继续循环向上判断是否还满足红黑树的原则。// 3.4:x节点的父节点是x节点祖父节点的右孩子,x节点的做叔叔为黑节点(或为空)// 仍然分两种情况,判断x节点是左孩子还是右孩子// 3.4.1如果x节点是左孩子,则将x节点的父节点进行右旋,右旋后x的父节点为x的右孩子,符合3.4.2的情形,再按3.4.2执行// 3.4.2如果x节点是右孩子,则将x节点的父节点变为黑节点,x节点的祖父节点变为红节点,然后对x节点的祖父节点进行左旋static TreeNode balanceInsertion(TreeNode root,TreeNode x) {//新插入的节点都是红节点x.red = true;//死循环判断,几个变量的含义分别为//xp:x节点的父节点,xpp:x节点的祖父节点//xppl:x节点祖父节点的左孩子节点(即x的左叔叔)//xppr:x节点祖父节点的右孩子节点(即x的右叔叔)for (TreeNode xp, xpp, xppl, xppr;;) {//x节点的parent为null,说明x节点是根节点(情形1)if ((xp = x.parent) == null) {//根节点为黑节点,因此将x节点变色黑,并返回x.red = false;return x;}//不是根节点再判断xp是否为黑节点,如果x的父节点为黑节点(情形2),则不用做任何平衡,因为此时并不违反红黑树的规则//x节点的祖父节点为null,此时也不做任何调整,此时说明x是根节点的孩子节点,而根节点是黑节点,因此也不违反红黑树的规则else if (!xp.red || (xpp = xp.parent) == null)return root;//如果x的父节点是x的祖父节点的左孩子,走到这个if说明x的父节点为红节点if (xp == (xppl = xpp.left)) {//判断判断x的右叔叔是否不为空且为红节点if ((xppr = xpp.right) != null && xppr.red) {//只需要做变色(情形3.1)//x的右叔叔节点调整为黑节点,x的父节点调整为黑节点,x的祖父节点调整为红节点xppr.red = false;xp.red = false;xpp.red = true;//将xpp作为x节点重新循环x = xpp;}//else的情况,x的右叔叔为空或为黑节点//此处需要注意,x的右叔叔为空或为黑节点是两种情况,虽然处理方式是一样的//x的右叔叔为空,是首次循环,x为插入节点时的情况,必然是这样,否则插入之前的树就不符合红黑树规则了。// 举例说明:假设此时右叔叔不为空,其黑高为n,则x的父节点的黑高必须为n,且n>=1(性质5决定)// 由于x的父节点为一个红节点,因此x的父节点必须存在两个黑高为n的子树// 显然这是不可能的,因为在x节点插入之前x的父节点必然存在一个Nil节点(黑高为0)//x的右叔叔为黑节点的情况必然不是首次循环(x为插入节点)的情况,//这种情况适用于x是经过变色后,由黑节点变为红节点,并再次进入循环后,才可能出现//可以看一下整个循环体的代码,只有3.1的情况才会导致该情况出现,3.1中将x的祖父节点变为红节点后,x指向了其祖父节点,并进行下一次循环//虽然是两种情况,但可以用同一种方法来处理else {//如果x是其父节点的右孩子(情形3.2.1)if (x == xp.right) {//进行左旋操作,并将xp节点作为x节点root = rotateLeft(root, x = xp);//xp节点作为x节点后,重新理顺xpp,xp的关系xpp = (xp = x.parent) == null ? null : xp.parent;}//如果x节点是其父节点的左孩子(情形3.2.2),直接执行这个if判断//经过上面的if内部逻辑调整后,"x是其父节点的右孩子"这种情况已调整为"x是其父节点的左孩子",再执行下面的右旋if (xp != null) {//xp节点变为黑节点xp.red = false;if (xpp != null) {//xpp节点变为红节点xpp.red = true;//将xpp节点进行右旋root = rotateRight(root, xpp);}}}}else {//情形3.3if (xppl != null && xppl.red) {xppl.red = false;xp.red = false;xpp.red = true;x = xpp;}else {if (x == xp.left) {//情形3.4.1root = rotateRight(root, x = xp);xpp = (xp = x.parent) == null ? null : xp.parent;}if (xp != null) {//情形3.4.2xp.red = false;if (xpp != null) {xpp.red = true;root = rotateLeft(root, xpp);}}}}}} 本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!