机器学习中对变量数据进行Log变化
机器学习算法中,一些算法要求数据符合正态分布,但是对于一些标签和特征来说,分布不一定符合正态分布,这个要怎么处理呢?
一个现在比较常见的方式是将数据进行Log变换,即取对数,这样可以使得数据在一定程度上符合正态分布的特征。
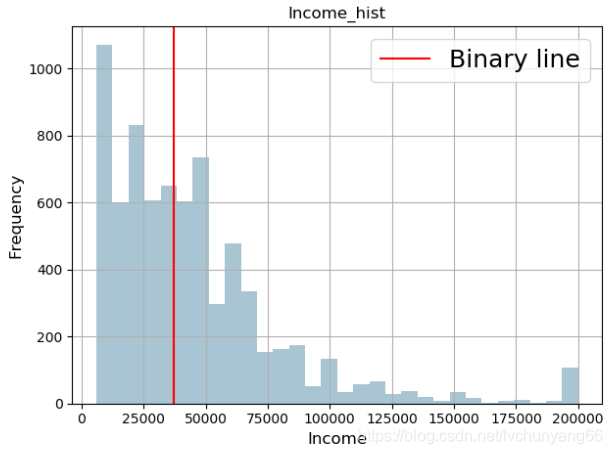
效果如下图所示:
(转换前)
(转换后)
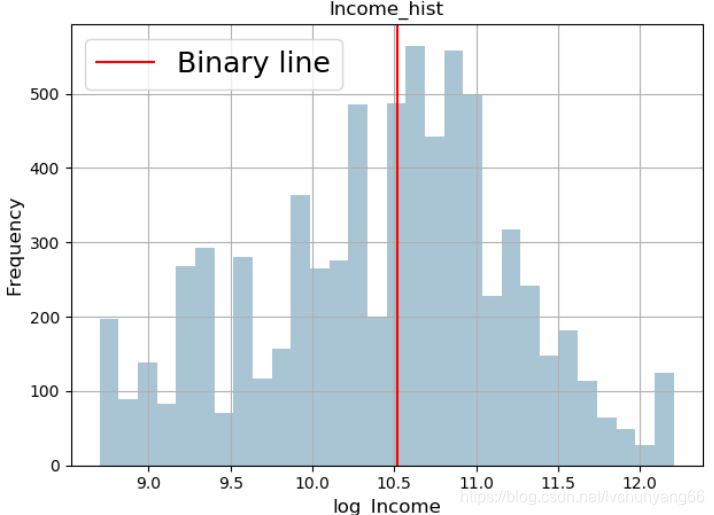
计算偏度较大的features
偏度,是统计数据分布偏斜方向和程度的度量,是统计数据分布非对称程度的数字特征。偏度亦称偏态,偏态系数。
其计算公式为:
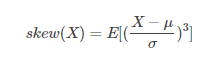
在python中用skew()计算特征分布的偏度,
#log transform skewed numeric features:
#找出df中数值型的变量
numeric_feats = all_data.dtypes[all_data.dtypes != 'object'].index
skewed_feats = all_data[numeric_feats].apply(lambda x: skew(x.dropna()))
#compute skewness
#计算偏度,找出df中数值型变量中,偏度大于0.75这个阈值的特征
skewed_feats = skewed_feats[skewed_feats > 0.75]
skewed_feats = skewed_feats.index
#对偏度较大的特征数据进行Log1p()转换。
all_data[skewed_feats] = np.log1p(all_data[skewed_feats])
数据Log变化
-
数据预处理时首先可以对偏度比较大的数据用log1p()函数进行转化,使其更加服从高斯分布,此步处理可能会使我们后续的分类结果得到一个好的结果。
-
平滑问题很容易处理掉,导致模型的结果达不到一定的标准,log1p( )能够避免复值得问题 — 复值指一个自变量对应多个因变量
log1p( ) 的使用就像是一个数据压缩到了一个区间,与数据的标准类似。其逆运算就是expm1的函数
由于使用的log1p()对数据进行了压缩,最后需要将预测出的平滑数据进行一个还原,而还原过程就是log1p的逆运算expm1.
log1p = log(x+1)
当x较大时直接计算,当x较小时用泰勒展开式计算
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!