基于PID和LQR的四旋翼无人机控制系统研究附matlab代码

✅作者简介：热爱科研的Matlab仿真开发者，修心和技术同步精进，matlab项目合作可私信。

🍎个人主页：Matlab科研工作室

🍊个人信条：格物致知。

更多Matlab仿真内容点击👇

智能优化算法       神经网络预测       雷达通信       无线传感器        电力系统

信号处理              图像处理               路径规划       元胞自动机        无人机 

⛄ 内容介绍

为提高四旋翼无人机的飞行稳定性,无人飞行器控制系统的鲁棒性和控制精度,以建立的四旋翼无人机飞行控制系统模型为基础,采用现代控制理论与传统控制论相结合的方法,针对姿态角速率,姿态角分别设计内环LQR(线性二次型调节器)控制器,及外环PID控制的双回路闭环控制器.充分利用PID控制器易于掌握且对模型要求精度低,LQR控制器能改善内回路的动态特性和稳态性能的特点,完成四旋翼无人机的飞行控制.通过实验遴选该双闭环控制器相关参数并进行优化,实验结果表明所设计的双回路控制器控制性能指标良好.

基于线性二次型调节器（Linear Quadratic Regulator，LQR）可以实现无人机的飞行控制。LQR是一种经典的优化控制方法，通过使用状态反馈和状态估计，以最小化给定性能指标为目标，设计飞行控制器。

以下是基于LQR实现无人机飞行控制的基本步骤：

1. 系统建模：需要对无人机的动力学进行建模，包括考虑飞行器的运动方程、状态空间表示等。这可以通过多旋翼或固定翼飞行器的物理特征和运数学模型。

2. 状态空间表示：将系统的运动方程转化为状态空间形式，得到状态方程： ẋ = Ax + Bu 其中，x是状态向量，A和B是系统的状态矩阵。

3. 性能评价指标：定义评价指标，如飞行稳定性、姿态跟踪精度等。根据指标选择适当的性能函数，常用的是二次型性能函数。

4. 设计LQR控制器：根据系统模型和性能指标，设计LQR控制器的增益矩阵K。LQR通过最小化状态误差和控制输入的二次代价函数来获得最优控制策略。使用方法，可以通过求解Riccati方程或优化算法来计算K矩阵。

5. 状态反馈控值，使用状态反馈控制律： u = -Kx 这将利用LQR设计的增益矩阵对系统进行控制。其中，u是控制输入向量。

6. 闭环控制：将状态反馈控制与状态估计器结合，实现无人机的闭环控制。通过续地测量、更新和修正状态，以实现稳定的飞行控制。

⛄ 部分代码

​%% declarationscT = 1.3529e-06 ;cQ = 2.1113*1e-08 ;l = 110*1e-3 ;lp = sqrt(2)/2*l ;m = 0.536 ;g = 9.81 ;rho_ground = 1.4 ;rotor_radius = 6.0*1e-2 ;hauteur_rotor = 29.3*1e-3 ;Ix = 0.029125 ;Iy = 0.029125 ;Iz = 0.055225 ;Kv_motor = 1750 ;Kv_motor_rad = Kv_motor*2*pi/60 ;km = 1/Kv_motor_rad ;Jr = 1.2991*1e-05 ;R = 0.07 ;U_sat = 12 ;Mx = [  cT cT cT cT ;        -cT*lp cT*lp cT*lp -cT*lp ;        -cT*lp -cT*lp cT*lp cT*lp ;        cQ -cQ cQ -cQ ] ;​%% Dynamic systemA = [0 0 0 1 0 0 0 0 0 0 0 0; %1     0 0 0 0 1 0 0 0 0 0 0 0; %2     0 0 0 0 0 1 0 0 0 0 0 0; %3     0 0 0 0 0 0 0 g 0 0 0 0; %4     0 0 0 0 0 0 -g 0 0 0 0 0; %5     0 0 0 0 0 0 0 0 0 0 0 0; %6     0 0 0 0 0 0 0 0 0 1 0 1; %7     0 0 0 0 0 0 0 0 0 0 1 0; %8     0 0 0 0 0 0 0 0 0 0 1 1; %9     0 0 0 0 0 0 0 0 0 0 (Iz-Iy)/Ix (Iz-Iy)/Ix; %10     0 0 0 0 0 0 0 0 0 (Ix-Iz)/Iy 0 (Ix-Iz)/Iy; %11     0 0 0 0 0 0 0 0 0 (Iy-Ix)/Iz (Iy-Ix)/Iz 0; %12       ];​B = [ 0 0 0 0;    0 0 0 0;    0 0 0 0;    0 0 0 0;    0 0 0 0;    0 0 0 1/m;    0 0 0 0;    0 0 0 0;    0 0 0 0;    1/Ix 0 0 0;    0 1/Iy 0 0;    0 0 1/Iz 0;    ];helix = [];Xeq =  [100 100 100 0 0 0 0 0 0 0 0 0];Xref = [100 100 100 0 0 0 ];​%% Position velocityApv = [ 0 0 0 1 0 0;        0 0 0 0 1 0;        0 0 0 0 0 1;        0 0 0 0 0 0;        0 0 0 0 0 0;        0 0 0 0 0 0;    ];Bpv = [ 0 0 0 0;        0 0 0 0;        0 0 0 0;        0 g 0 0;        -g 0 0 0;        0 0 0 1/m;    ];Qpv = [1 0 0 0 0 0;       0 1 0 0 0 0;       0 0 1 0 0 0;       0 0 0 50 0 0;       0 0 0 0 50 0;       0 0 0 0 0 50];Rpv = [20 0 0 0;       0 20 0 0;       0 0 1 0;       0 0 0 1];   [Kpv,S,E] = lqr(Apv,Bpv,Qpv,Rpv);​%% Angle velocityAang = zeros(3,3);Bang = [1/Ix 0 0;        0 1/Iy 0;        0 0 1/Iz;        ];Qang = [1 0 0;       0 1 0;       0 0 1];Rang = [0.05 0 0;       0 0.05 0;       0 0 0.05];[Kang,S,E] = lqr(Aang,Bang,Qang,Rang);    %% Euler anglesAeu = zeros(3,3);Beu = eye(3);Qeu = [1 0 0;       0 1 0;       0 0 1];Reu = [1 0 0;       0 1 0;       0 0 1];[Keu,S,E] = lqr(Aeu,Beu,Qeu,Reu);​​

⛄ 运行结果

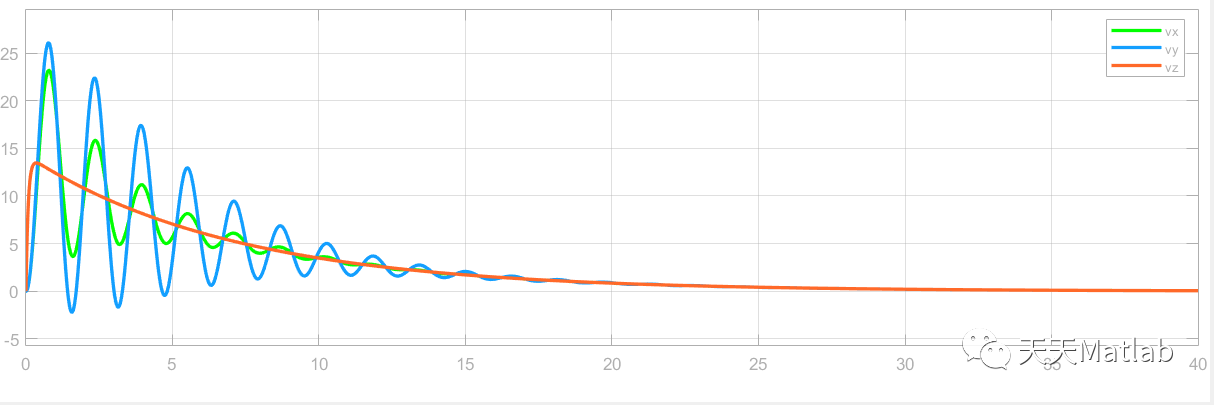
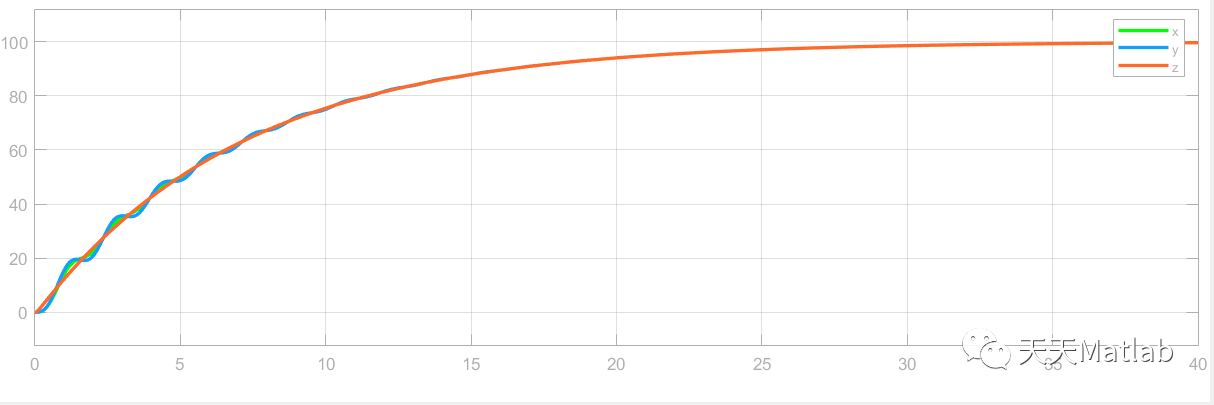
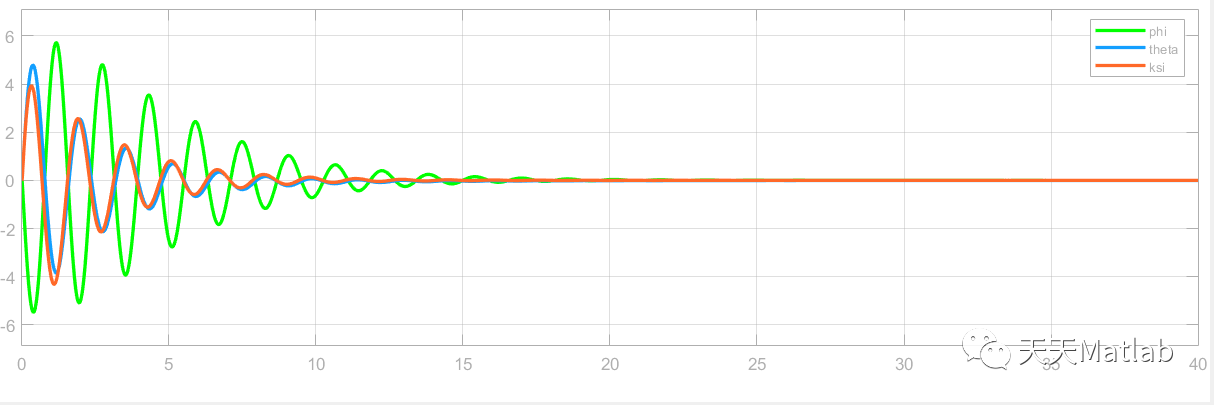
⛄ 参考文献

[1] 马敏,许中冲,常辰飞,等.基于PID和LQR的四旋翼无人机控制系统研究[J].测控技术, 2016, 35(10):5.DOI:10.3969/j.issn.1000-8829.2016.10.011.

[2] 黄丹,周少武,吴新开,等.基于LQR最优调节器的倒立摆控制系统[J].微计算机信息, 2004, 20(2):3.DOI:10.3969/j.issn.1008-0570.2004.02.018.

⛳️ 代码获取关注我

❤️部分理论引用网络文献，若有侵权联系博主删除

❤️ 关注我领取海量matlab电子书和数学建模资料

🍅 仿真咨询

1.卷积神经网络（CNN）、LSTM、支持向量机（SVM）、最小二乘支持向量机（LSSVM）、极限学习机（ELM）、核极限学习机（KELM）、BP、RBF、宽度学习、DBN、RF、RBF、DELM实现风电预测、光伏预测、电池寿命预测、辐射源识别、交通流预测、负荷预测、股价预测、PM2.5浓度预测、电池健康状态预测、水体光学参数反演、NLOS信号识别、地铁停车精准预测、变压器故障诊断

2.图像识别、图像分割、图像检测、图像隐藏、图像配准、图像拼接、图像融合、图像增强、图像压缩感知

3.旅行商问题（TSP）、车辆路径问题（VRP、MVRP、CVRP、VRPTW等）、无人机三维路径规划、无人机协同、无人机编队、机器人路径规划、栅格地图路径规划、多式联运运输问题、车辆协同无人机路径规划

4.无人机路径规划、无人机控制、无人机编队、无人机协同、无人机任务分配

5.传感器部署优化、通信协议优化、路由优化、目标定位

6.信号识别、信号加密、信号去噪、信号增强、雷达信号处理、信号水印嵌入提取、肌电信号、脑电信号

7.生产调度、经济调度、装配线调度、充电优化、车间调度、发车优化、水库调度、三维装箱、物流选址、货位优化

8.微电网优化、无功优化、配电网重构、储能配置

9.元胞自动机交通流 人群疏散 病毒扩散 晶体生长

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！