JZ4-重建二叉树

【题目描述】
输入某二叉树的前序遍历和中序遍历的结果，请重建出该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。
eg. 例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6}，则重建二叉树并返回。

【二叉树的补充知识】

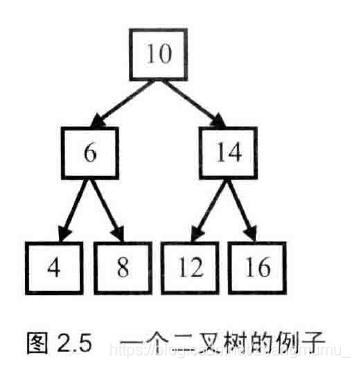
• 前序遍历：先访问根节点，再访问左子节点，最后访问右子节点。图2.5中的二叉树前序遍历顺序是10、6、4、8、14、12、16。
• 中序遍历：先访问左子节点，再访问根节点，最后访问右子节点。图2.5中的二叉树中序遍历顺序是4、6、8、10、12、14、16。
• 后序遍历：先访问左子节点，再访问右子节点，最后访问根节点。图2.5中的二叉树后序遍历顺序是4、8、6、12、16、14、10。

【官方解法】
重点：前序和中序的特点及递归。
详细的思路步骤见注释！

/*** Definition for binary tree* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode(int x) : val(x), left(NULL), right(NULL) {}* };*/
class Solution {
public://这个函数等下在下面调用，配合官方给得初始api接口//函数的输入依次是前序数组、前序数组最左边元素下角标、最右边元素下角标、中序数组、中序数组最左边下角标、最右边下角标。TreeNode* rebuild(vector<int>& pre, int pre_left, int pre_right, vector<int>& vin, int vin_left, int vin_right) {if (pre_left > pre_right||vin_left > vin_right) return nullptr;//养成好习惯，判空操作 TreeNode* root = new TreeNode(pre[pre_left]);//树的根节点为前序数组第一个元素//在中序数组中进行遍历，直到找到与根节点元素值相同的值的下角标ifor (int i=vin_left; i<=vin_right; ++i) {if (vin[i] == root->val) {//将左子树与右子树找到后，进行递归操作。root->left = rebuild(pre, pre_left+1, pre_left+i-vin_left, vin, vin_left, i-1);root->right = rebuild(pre, pre_left+i-vin_left+1, pre_right, vin, i+1, vin_right);break;}}return root;}//官方给的api接口TreeNode* reConstructBinaryTree(vector<int> pre,vector<int> vin) {//调用rebuild函数return rebuild(pre, 0, pre.size()-1, vin, 0, vin.size()-1);}
};

【B站解法】
思路与官方一样，代码稍有不同。

/*** Definition for binary tree* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode(int x) : val(x), left(NULL), right(NULL) {}* };*/
class Solution {
public:unordered_map<int,int> pos;TreeNode* reConstructBinaryTree(vector<int> pre,vector<int> vin) {int n = pre.size();for(int i = 0; i < n; i ++)pos[vin[i]] = i;return dfs(pre, vin, 0, n - 1, 0, n - 1);}TreeNode* dfs(vector<int> pre,vector<int> vin, int pl, int pr, int vl, int vr){//前序 根左右  pre[pl]//中序 左根右if(pl > pr) return NULL;//找根节点TreeNode* root = new TreeNode(pre[pl]);//左子树的长度kint k = pos[pre[pl]] - vl;//vl + k 根节点root -> left = dfs(pre, vin, pl + 1, pl + k, vl, vl + k - 1);root -> right = dfs(pre, vin,pl + k + 1, pr, vl + k + 1, vr);return root;}};

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！