机器人学学习笔记（1）20211118

课程连接在此：【机器人理论最好中文入门课程 没有之一】 机械臂 系统 结构 旋转矩阵 变换矩阵 DH模型 运动学正逆解 轨迹规划 动力学 控制 遥控操作 教程_哔哩哔哩_bilibili

Chapter1—Spatial Representation and Transformation

1.1Position，Orientation and Frames

①Position Vector

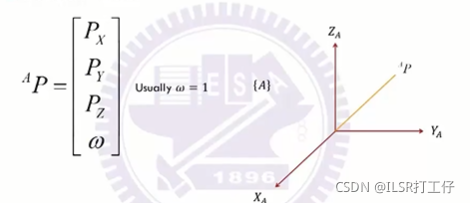
在A坐标系中表示p的位置

② Orientation 

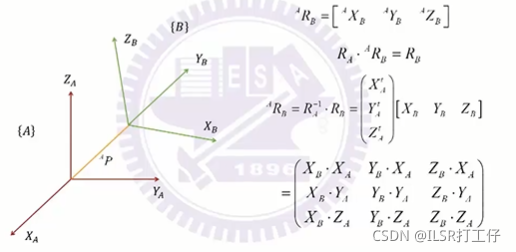
（9个元素有3个自由度是因为有6个限制因素：3*长度=1；3个向量两两互相垂直；）

旋转矩阵的范矩阵是其转置

1.2Mapping Between Frames 

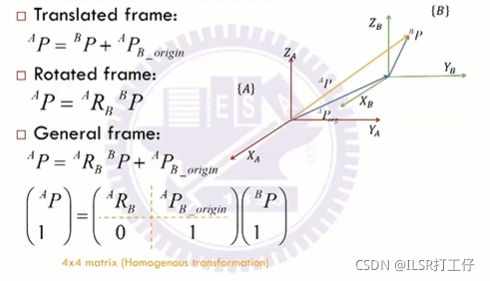
• 平行运动具有可交换性
• 旋转没有交换性

Rotation（not commutative）

 选择特殊轴（xyz）作为旋转轴——（把复杂系统变简单）分量彼此不会有关系

General

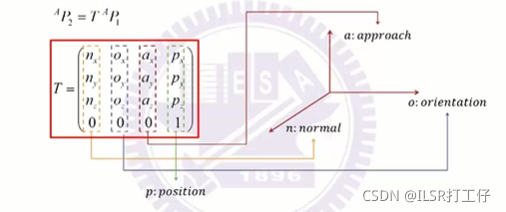
 顺着z轴转和移动z是最在意的方向，y是被选定的方向，x是在其基础上就定下来的

前乘与后乘的选择

后乘：A×B表示B相对于A旋转

前乘：B×A表示基座是世界坐标系

Compound

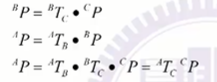
Inversion 

1.3 Transfomation

  General Rotstion Transformation

Rotation about an arbitrary vector k from origin

First find a coordinate frame C

Rotating T about is equivalent to rotating Xaround Z axis of frame C 

Given a rotational transformation R

1.4

Equate R to () 

Define Trace (A)=sum of diagonal components of matrix A 

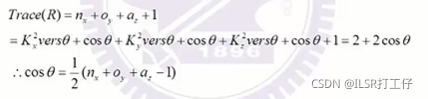
 接近0时，突变比较明显，所以在计算时计算量很大，因此选择tan

 有正负合理，有两个解。选择正号的，选择角度比较小的，整的时候小于180°

Another set：

 From the largest element of noa，the largest of k（xyz）can be determined

1.5Three Angle Rotation : Euler angles,RPY Angles

Euler Angels:

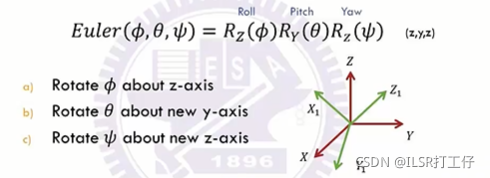
 当y轴转0时会出现退化

RPY Angels

 Euler transformation solution

 For Euler z-y-z

1.6 specification of position

Cylindrical Coordinates

**

 旋转轴和平移轴时可能会比较简单；

Spheriacal Coordiantes

 Summary

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！