张量网络编程学习笔记（3-2）：TN_Tutorial自动微分门量子线路的模块化编程：AD_Circuits/ADgate.py + /ADQC_QSP1.py + /ADQC_QSP2.py

文件参照 TN_Tutorial.AD_Circuits 的 ADgate.py，ADQC_QSP1.py，ADQC_QSP2.py

本文仅从本人复习需要出发：作为对首都师范大学冉仕举老师课程内容的整理、归纳以及补充

课程详情：张量网络PyThon编程：3.4 量子线路模块化编程(a) ADGate类_哔哩哔哩_bilibili

冉仕举老师本人空间：StringCNU的个人空间_哔哩哔哩_bilibili

github文件_TN_Tutorial：Add files via upload · ranshiju/Python-for-Tensor-Network-Tutorial@c76f4a2 (github.com)

* 模块化编程（1）- 系统地调用门（ADGate）：

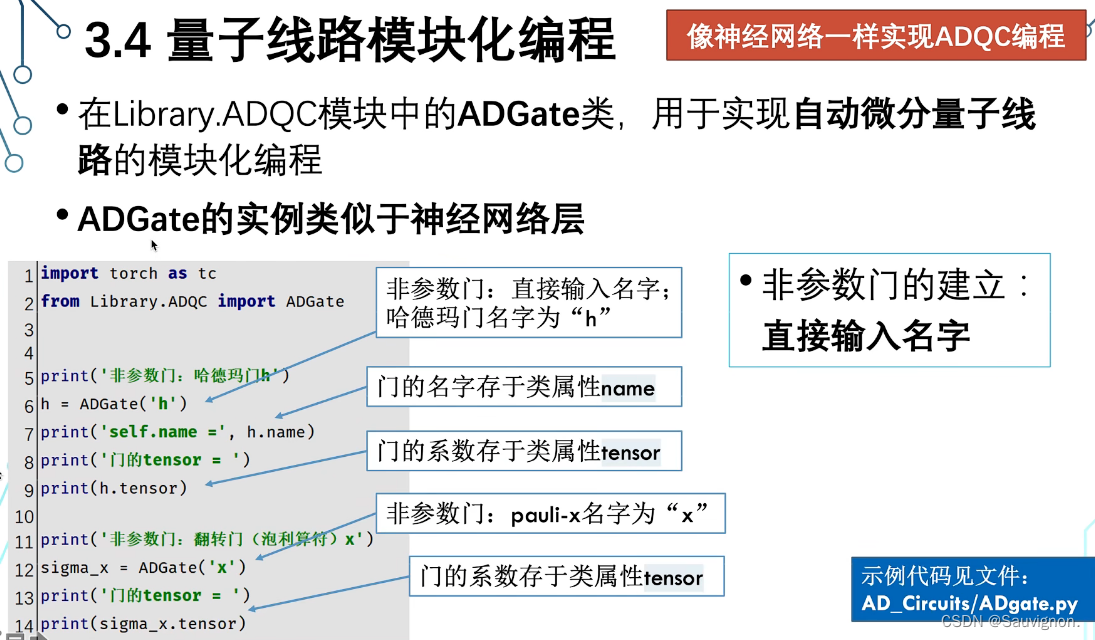
（1）ADQC怎样建立门的：(看源码)，重要属性：self.name, self.paras, self.tensor 变分or固定门

# ============================ 以下是非参数门，============================if self.name in ['x', 'y', 'z']:self.tensor = mf.pauli_operators(self.name)self.tensor = self.tensor.to(device=self.device, dtype=self.dtype)self.variational = Falseelif self.name in ['hadamard', 'h']:self.tensor = mf.hadamard()self.tensor = self.tensor.to(device=self.device, dtype=self.dtype)self.variational = Falseelif self.name in ['gate_no_variation']:self.paras = parasself.tensor = parasself.variational = False
# ============================ 以下是参数门，==============================elif self.name == 'rotate':if paras is None:self.paras = tc.randn((4, ))self.paras = self.paras.to(device=self.device)elif self.name in ['rotate_x', 'rotate_y', 'rotate_z', 'phase_shift']:if paras is None:self.paras = tc.randn(1)self.paras = self.paras.to(device=self.device)elif self.name == 'evolve_variational_mag':  # 单体磁场演化, shape=(2, )assert 'tau' in self.settingsassert 'h_directions' in self.settingsif paras is None:self.paras = tc.randn((len(self.settings['h_directions']), ))self.paras = self.paras.to(device=self.device, dtype=tc.float64)elif self.name == 'latent':if paras is None:if self.pos is None:ndim = 2else:ndim = len(self.pos)if qudit_dims is None:qudit_dims = [2] * ndimdim_t = math.prod(qudit_dims)if 'initial_way_latent' in self.settings:if self.settings['initial_way_latent'] == 'identity':self.paras = tc.eye(dim_t, dim_t) + 1e-5 * tc.randn((dim_t, dim_t))else:self.paras = tc.randn((dim_t, dim_t))self.paras = self.paras.to(device=self.device, dtype=self.dtype)elif self.name == 'arbitrary':  # 传入一个paras矩阵作为门assert type(paras) is tc.Tensorself.paras = paras.to(device=self.device, dtype=self.dtype)self.tensor = self.parasif self.variational:self.paras = nn.Parameter(self.paras, requires_grad=True)self.renew_gate()

更新门参数注意要赋值到 gate.paras.data =tc.tensor (...) ，paras有一个自动微分属性：除非手动将待传系数张量给赋予自动微分属性：tc.nn.Parameters(tc.tensor(...) ) , 加入require_grad = True

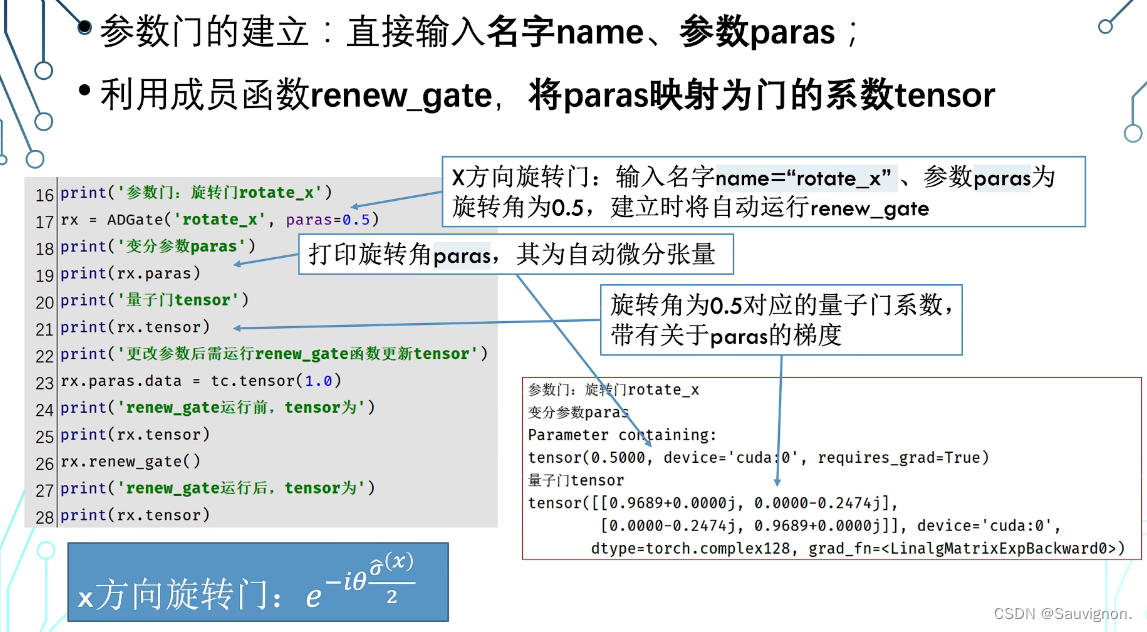
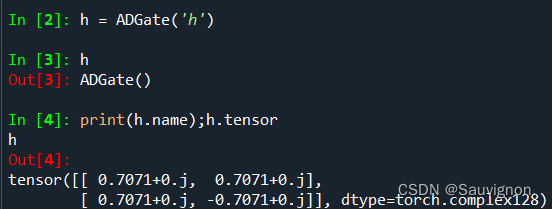
我们在命令行里测试一下：非参数门：hadamard

单参数门 ： rotate_x (0.5) ~ (1.0)

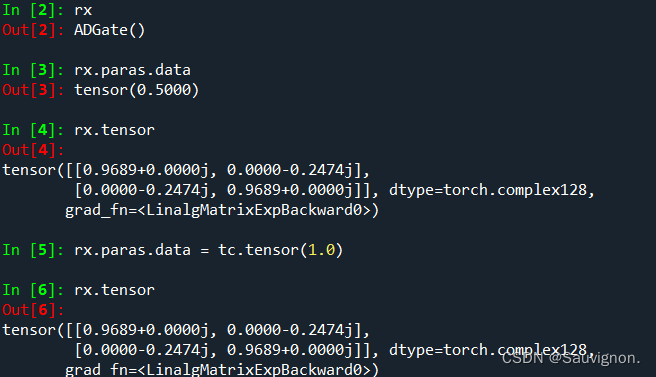
（注意，需要renew转角，否则就是临时储存在gate.paras.data里面）

 矩阵参数门：latent，arbitary（U4门）

     latent_gate 内部的自动更新.renew_gate( )  是怎么实现的 以及 初始化的特色：

        elif self.name == 'latent':# 无参数初始化if paras is None:# 默认二体门if self.pos is None:ndim = 2else:ndim = len(self.pos)# 默认2-qbitif qudit_dims is None:qudit_dims = [2] * ndimdim_t = math.prod(qudit_dims)if 'initial_way_latent' in self.settings:# 深层隐门网络,初始化建议是I + [ \epsilon ]# 这样可以缓解梯度消失if self.settings['initial_way_latent'] == 'identity':self.paras = tc.eye(dim_t, dim_t) + 1e-5 * tc.randn((dim_t, dim_t))else:self.paras = tc.randn((dim_t, dim_t))# 含参数初始化self.paras = self.paras.to(device=self.device, dtype=self.dtype)

  可本人测试了一下，肉眼单次看tensor好像两者规格上没有什么显著差别（）

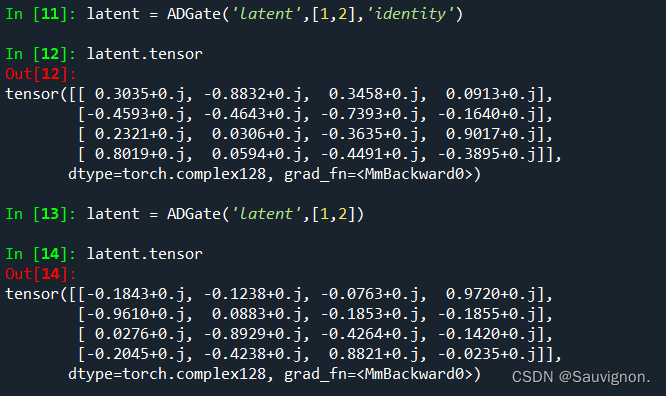
   U4 门暂且不测试了，，，

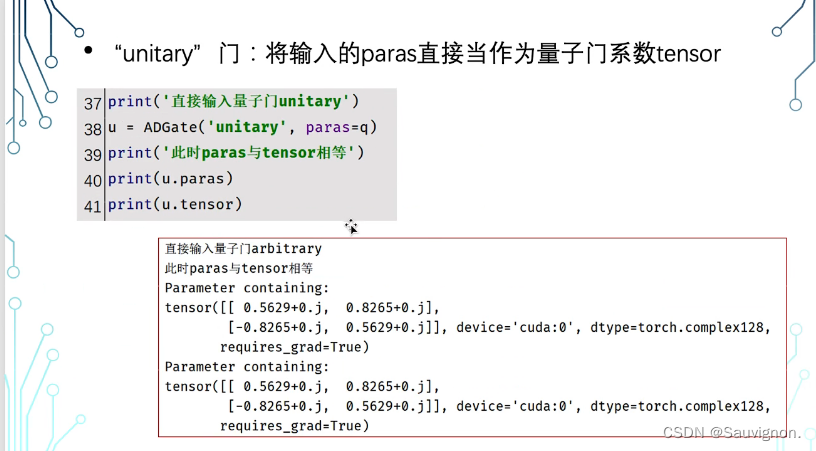
* 模块化编程（2）- 把一组门给打包：qc = ADQC.ADQC_basic 

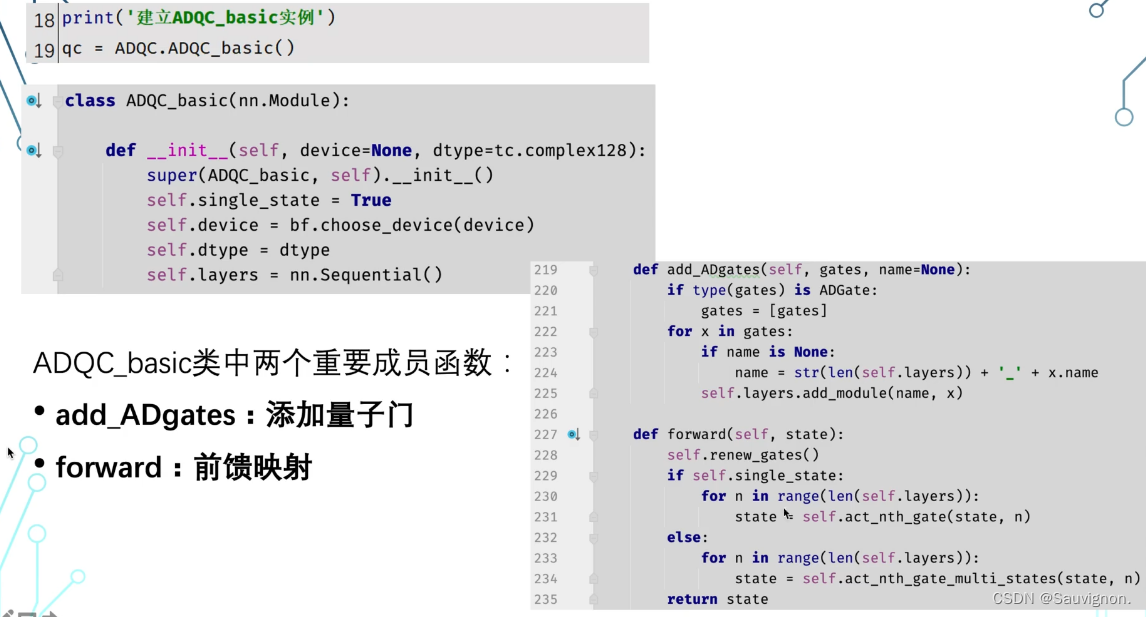
 回到态制备问题，如图例先是经典变分门线路 ：

  还是要先初始化量子态：

num_qubits = 3
# 初始化目标态
psi_target = tc.randn((2**num_qubits, ),dtype=tc.complex128, device=device)
psi_target /= psi_target.norm()
#--------------------------------------------------------------#
# 初始化量子态|000>,仅作示例,将在每一轮优化里重新定义一次
psi = state_all_up(n_qubit=num_qubits, d=2).to(device=device, dtype=psi_target.dtype)
psi = qc(psi)​

  逐行逐门添加的 （ADQC_QSP1.py）： 

# print('建立ADQC_basic实例')
qc = ADQC.ADQC_basic()
# print('在ADQC_basic实例中添加ADgate实例')
qc.add_ADgates(ADQC.ADGate('rotate', pos=0))
qc.add_ADgates(ADQC.ADGate('x', pos=1, pos_control=0))
qc.add_ADgates(ADQC.ADGate('rotate', pos=0))
qc.add_ADgates(ADQC.ADGate('rotate', pos=1))
qc.add_ADgates(ADQC.ADGate('x', pos=2, pos_control=1))
qc.add_ADgates(ADQC.ADGate('rotate', pos=1))
qc.add_ADgates(ADQC.ADGate('rotate', pos=2))
qc.add_ADgates(ADQC.ADGate('x', pos=0, pos_control=2))
qc.add_ADgates(ADQC.ADGate('rotate', pos=2))# print('打印各个门及变分参数')
for x in qc.state_dict():print(x, qc.state_dict()[x])

  有封装好的 全latent_gate 线路（ADQC_QSP2.py） ：

num_qubits = 3​# print('建立ADQC_basic实例')
qc = ADQC.ADQC_LatentGates(# 其实 lattice='brick' or 'stair',# 两种选择等价lattice = 'brick',num_q = num_qubits,depth = 2)
# print('每层二体门作用的位置为：')
print(qc.pos)
# 会返回：[[0, 1], [1, 2]]# print('ADQC的变分参数维数为：')
for x in qc.state_dict():print(qc.state_dict()[x].shape)​

搭建基于ADQC_latent的分类器，有封装好的线路（ADQC_iris数据集分类）：

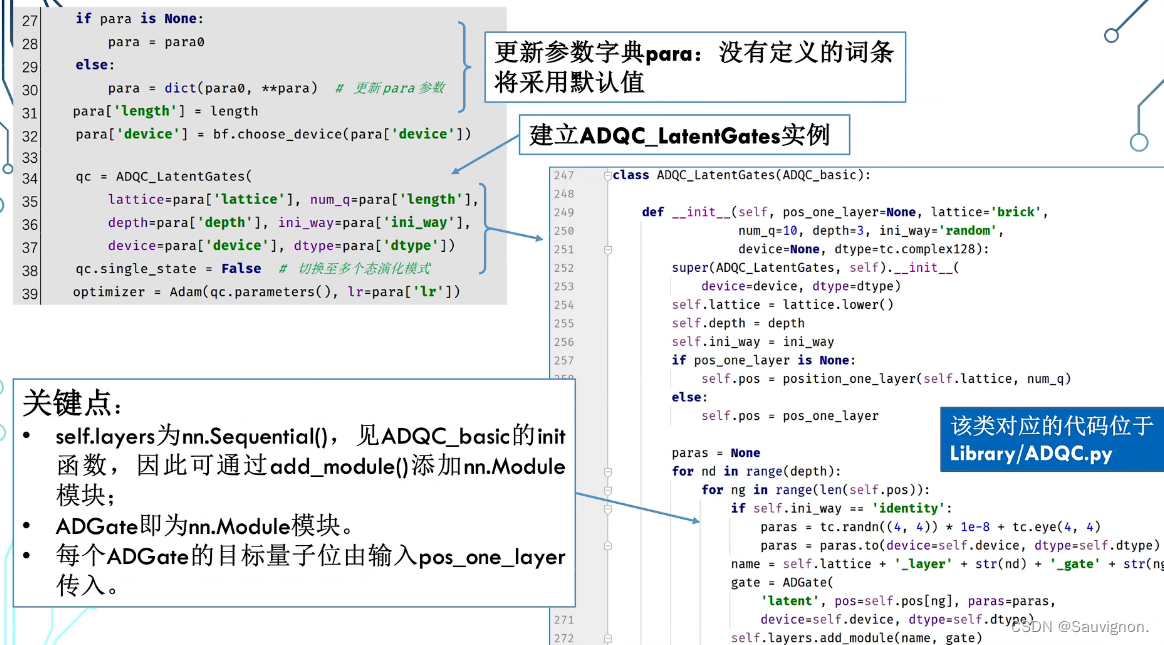
实现ADQC_LatentGates对线路的打包：开两个循环 nd 和 ng ：

逐深度与逐层对 LatentGates进行添加

向 nn.Sequential 写入 add_module() ：ADGate，是用 nn.Module建立的实例

这些参数是量子门的变分参数。self.Layers,作为储存全部量子门的属性，由Sequential建立

 运行属性的原理（single_state），我们留在下一节细讲：

毕竟是变分算法，实现参数更新：向前传播 + optimizer + 反向传播 ~ 写法类似于神经网络：

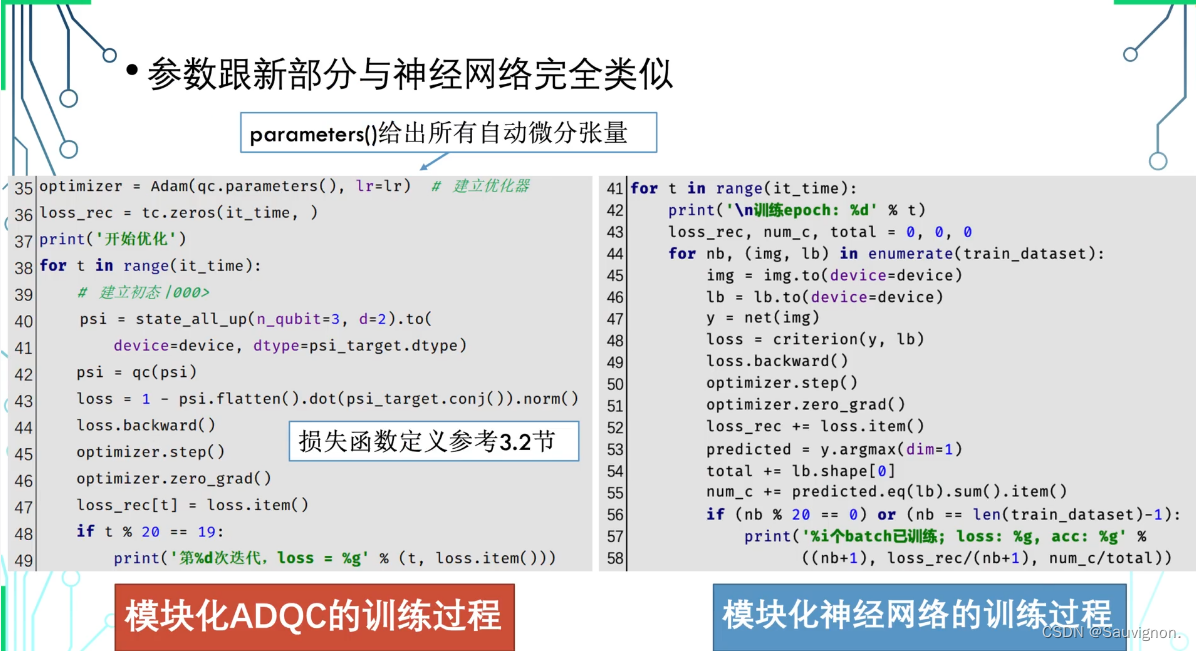
注释一下：ADQC训练过程 

optimizer = Adam(qc.parameters(), lr=lr)  # 建立优化器
loss_rec = tc.zeros(it_time, )
# 储存 loss_rec,后面打印
print('开始优化')
for t in range(it_time):# 建立初态|000>psi = state_all_up(n_qubit=num_qubits, d=2).to(device=device, dtype=psi_target.dtype)psi = qc(psi)# 向前传播,同：qc,forward(psi)loss = 1 - psi.flatten().dot(psi_target.conj()).norm()loss.backward()optimizer.step()optimizer.zero_grad()loss_rec[t] = loss.item()if t % 20 == 19:print('第%d次迭代，loss = %g' % (t, loss.item()))

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！