NOIP 2021 数列 解题报告
原题目如下：
洛谷有相应题目，链接[NOIP2021] 数列 - 洛谷
根据题目，直观的想法，首先计算出所有合法的序列{ai}，对于每一个合法序列求出对应权值，最后求总。于是简单的求法，就是枚举所有的序列，判断是否合法，合法就求出权值。每个ai有m+1种选择，总共枚举量是(m+1)n, 判断合法是O(n)的复杂度，求权值也是O(n)，总复杂度O(n*mn)。题目的数据范围，1 ≤ k ≤ n ≤ 30，0 ≤ m ≤ 100，1≤vi≤998244353。这么大的数据量，指数复杂度，显然是不可行的。所以需要仔细分析下题目的数学特性。
分析数学问题，最简单的思路是从限制入手，条件越多，限制越多，往往就越简单。题目有几个限制：
- ai取值范围在0~m。这个条件可以理解为，从0~m中取n个数，可以重复取数。
- S的二进制表示1的个数不超过k。由
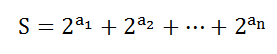，可以看出，当ai = c时，实际上是在S的第c位置1，如果有ai = aj = c，那么就会产生进位，使得第c+1位为1。这个性质很重要，因为，进位只会向高位进位。那么我们分析问题，是否就可以从最低位分析起，一步一步往高位分析？毕竟高位的进位不会影响低位，所以问题只需往一个方向（高位）推进。
让我们先考虑S的第0位，亦即从0-m中取到0的情况。
1）如果0不取，那么问题直接缩减为1~m中取n个数的子问题。
2）如果只取了一个0，那么S的第0位为1，S里的其他位置，最多只能有k-1个位为1。问题缩减为，从1~m中取出n-1个数，使得S的第1位以上的所有位，最多只有k-1个1。这样取数能有多少种不同的取数方式。这样问题规模就变小了。再考虑上到底是哪个ai = 0就可以了。
3）如果取了多个0，比如3个，那么S的最后2位都为1了，这时发现问题稍微复杂了点。因为第1位以上的二进制位被置为1了，那么问题规模缩小之后，与原问题就不是完全一样。（原问题S的所有位刚开始都是0）。所以需要记录哪些位已经被置1。这其实就是动态规划里常用的“状态压缩”方法。就是递推到子问题时候，需要记录S的初始状态。S最多位数为m + ceil(logn)（如果全部ai都选择m，那么就会一直进位到第logn位），m=100，状态太多，没法记录。不够好在logn很小，n=30，logn上取整也就是5。而我们是从低位一步一步往高位递推的，那么进位最多也就往高位进位到第5位。这完全可以记录下来。
经过以上分析，整个解题思路就清晰了。用递推可以解决这问题。从ai=m开始，往ai=0递推。递推到第Vi时，记录当前S第i位以上还能有多少位可以置1，S第i位以上有哪些位初始状态已经置1即可。完整解法如下。
令g [i][n’][k’][s’] 表示，当S的第i ~ i+5位初始状态为s’的情况下，从i~m中取n’个数（可重复取），取数后S为1的位的个数不超过k’。此时，合法数列{ai}的方案总数。有
公式中除法为下取整，C(n’, j)为组合公式，即从n’个数中取j个数，有多少种取法。因为数列{ai}是有序的，选择了j个i之后，需要选定数列的哪j个值为i。但是题中要求求得权值和，仅仅有方案总数是不够的。需要在计算方案总数时候顺带把权值和计算好了。权值为Vai的连乘，乘法是符合分配率的。用p[i][n’][k’][s’] 表示 g [i][n’][k’][s’]对应的某个具体方案。我们递推时，先考虑i取多少个数，再递推，比如i取c个数，那么对应的子方案即为 {i}*c + p[i+1][n’-c] （此处忽略后两维信息，不影响分析）。子方案的权值为 w[i+1]，那么p[i][n’][k’][s’]的权值即为 Vi^c * w[i+1]。如果有多个子方案，比如w1, w2, w3等，那么总的权值之和就是 Vi^c * w1 + Vi^c * w2 + Vi^c * w3 + … = Vi^c * (w1 + w2 + … )。也就是说，可以先计算出子问题的权值之和，再直接乘以Vi即可。
设f [i][n’][k’][s’] 表示 g [i][n’][k’][s’] 对应所有方案的权值之和，那么
f [0][n][k][0] 即为问题答案。计算过程中记得取模就行。状态总数m*n*k*n，状态转移计算量为O(n)，总的复杂度为O(m*n^4)，对于题目数据量没问题。
本人微信公众号也发布了相同文章：NOIP2021“数列”解题报告
程序：（因为f[i]只需要依赖到f[i+1]，用滚动数组节约空间）
#include
#include
#define NN 103
#define NN2 32
#define MM 998244353
#define I64 long longI64 f[2][NN2][NN2][NN2];
I64 (*f1)[NN2][NN2], (*f2)[NN2][NN2];
I64 pow_v[NN][NN2];void cal_c_powv(I64 c[][NN2], int v[], int m, int n)
{int i, j;c[0][0] = 1;for (i=1; i=0; i--){I64 (*tmp)[NN2][NN2] = f1;f1 = f2; f2 = tmp;memset(f2, 0, sizeof(I64)*NN2*NN2*NN2);f2[0][0][0] = 1;for (n=0; n<=N; n++) for (k=1; k<=K; k++) for (s=0; s<=(N-n)/2; s++){for (j=0; j<=n; j++) {f2[n][k][s] += pow_v[i][j]*f1[n-j][k-(s+j)%2][(s+j)/2]%MM*c[n][j]%MM;}f2[n][k][s] %= MM;}}printf("%lld\n", f2[N][K][0]);return 0;
}
本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！