iOS LeetCode ☞ 最大正方形

在一个由 '0' 和 '1' 组成的二维矩阵内，找到只包含 '1' 的最大正方形，并返回其面积。

示例 1：

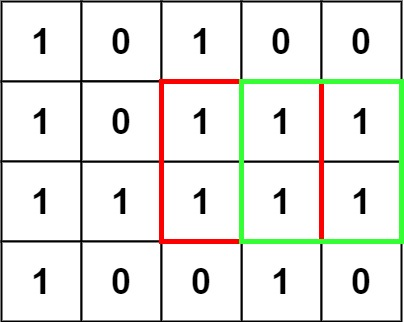
输入：matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]]
输出：4

示例 2：

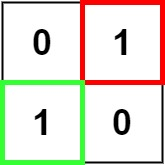
输入：matrix = [["0","1"],["1","0"]]
输出：1

示例 3：

输入：matrix = [["0"]]
输出：0

提示：

• m == matrix.length
• n == matrix[i].length
• 1 <= m, n <= 300
• matrix[i][j] 为 '0' 或 '1'

解题思路

我们用 dp(i, j) 表示以 (i, j) 为右下角，且只包含 1 的正方形的边长最大值。如果我们能计算出所有 dp(i, j) 的值，那么其中的最大值即为矩阵中只包含 1 的正方形的边长最大值，其平方即为最大正方形的面积。

那么如何计算 dp 中的每个元素值呢？对于每个位置 (i, j)，检查在矩阵中该位置的值：

• 如果该位置的值是 0，则 dp(i, j) = 0，因为当前位置不可能在由 1 组成的正方形中；

• 如果该位置的值是 1，则 dp(i, j) 的值由其上方、左方和左上方的三个相邻位置的 dp 值决定。具体而言，当前位置的元素值等于三个相邻位置的元素中的最小值加 11，状态转移方程如下：
  dp(i, j) = min(dp(i - 1, j), dp(i - 1, j - 1), dp(i, j - 1)) + 1

• 此外，还需要考虑边界条件。如果 i 和 j 中至少有一个为 0，则以位置 (i, j) 为右下角的最大正方形的边长只能是 1，因此 dp(i, j) = 1。

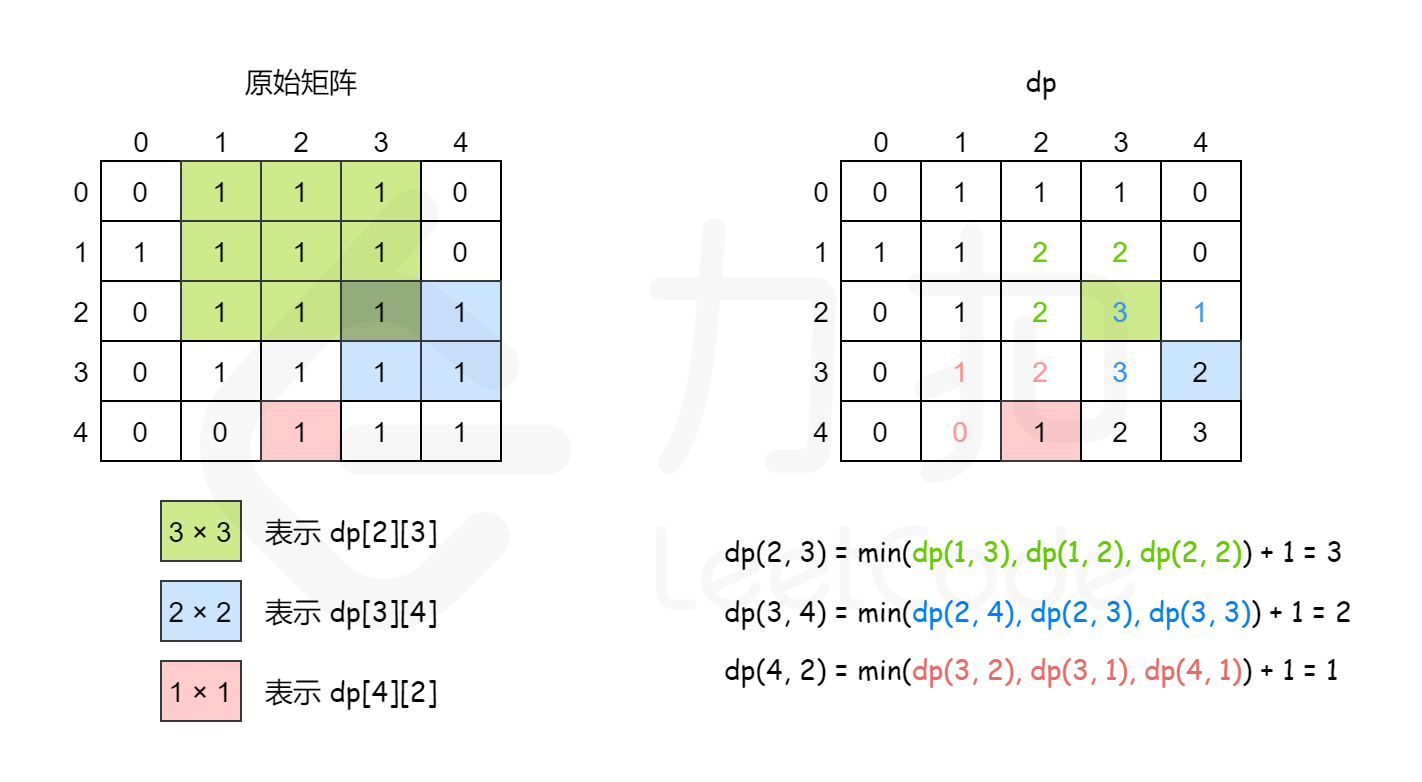
以下用一个例子具体说明。原始矩阵如下。

0 1 1 1 0
1 1 1 1 0
0 1 1 1 1
0 1 1 1 1
0 0 1 1 1

对应的 dp 值如下。

0 1 1 1 0
1 1 2 2 0
0 1 2 3 1
0 1 2 3 2
0 0 1 2 3

下图也给出了计算 dp 值的过程。

代码

	// 221. 最大正方形func maximalSquare(_ matrix: [[Character]]) -> Int {var maxSide = 0if matrix.count == 0 || matrix[0].count == 0 {return maxSide}let rows = matrix.count, columns = matrix[0].countvar dp = [[Int]](repeating: [Int](repeating: 0, count: columns), count: rows)for i in 0..<rows {for j in 0..<columns {if matrix[i][j] == "1" {if i == 0 || j == 0 {dp[i][j] = 1} else {dp[i][j] = min(min(dp[i - 1][j], dp[i][j - 1]), dp[i - 1][j - 1]) + 1}maxSide = max(maxSide, dp[i][j])}}}return maxSide * maxSide}

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！