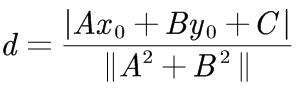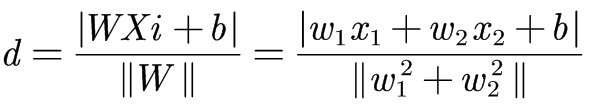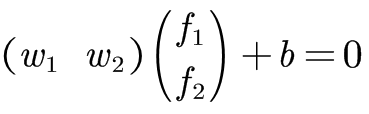【机器学习】支持向量机 SVM 原理详解 详细数学推导

前排提示 多公式预警，如果想真正掌握、想对SVM的推导和原理理解透彻，就请耐心的看完推导过程，博主发现很多书籍文献资料上推导过程大多有所省略，这对数学基础不牢靠的同学来说不太友好（比如博主自己 - -#），所以在此给出最细致的推导过程。

由于公式符号繁多，博主也经过了多次修正检查，如有疏漏或不对的地方还请指正（公式编辑真的打的累死惹）~~

支持向量机 SVM(support vector machine)算法原理：

（首先给出一个图，svm最终目的就是要求解图中的超平面g，也叫决策边界。其中样本G,R,S可称为 支持向量）

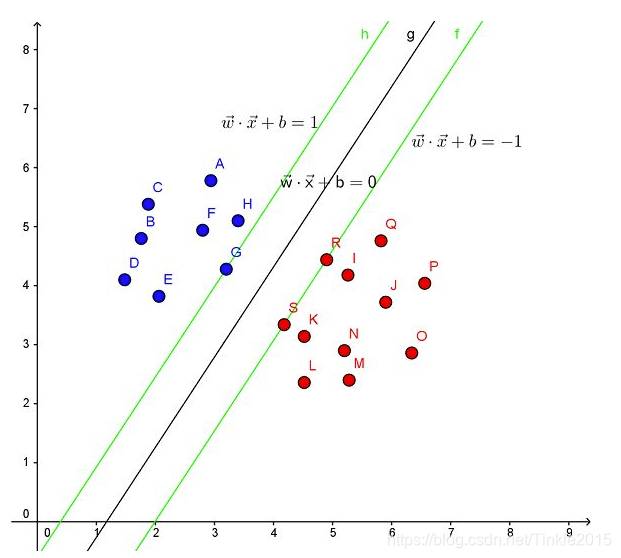
        将含两种类别的样本空间通过一个决策边界分开，使得离决策边界最近的样本点能够尽可能远离决策边界 (通俗理解：找到一条线，使得离该线最近的点能够最远)，下面直接进入正题开始推导：

    1.点面距离公式 =》svm的中最优解问题：
    ===》几何公式：
        点（x0，y0）到直线 Ax + By + C = 0 的距离   
    ===》样本空间下描述:（含x轴y轴的二维平面，等价于 含两种特征的样本空间）
        在含两种特征f1,f2的样本空间中，

        某个样本点Xi(特征f1 = x1,特征f2 = x2) 与某个特征划分边界D: w1f1 +w2f2 + b = 0 的欧氏距离为：

       
        将特征划分边界 写成向量形式=》
        其中,F=(f1,f2)表示样本空间中各个维度的特征,样本点        【0.3】

    ===》样本空间  推广至N维：
        N维特征空间有样本点

        特征划分平面D': w1'f1'+w2'f2'+...+wn'fn' +  b' = 0 即 ： 
                【0.4】
    决策方程的变换&

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！