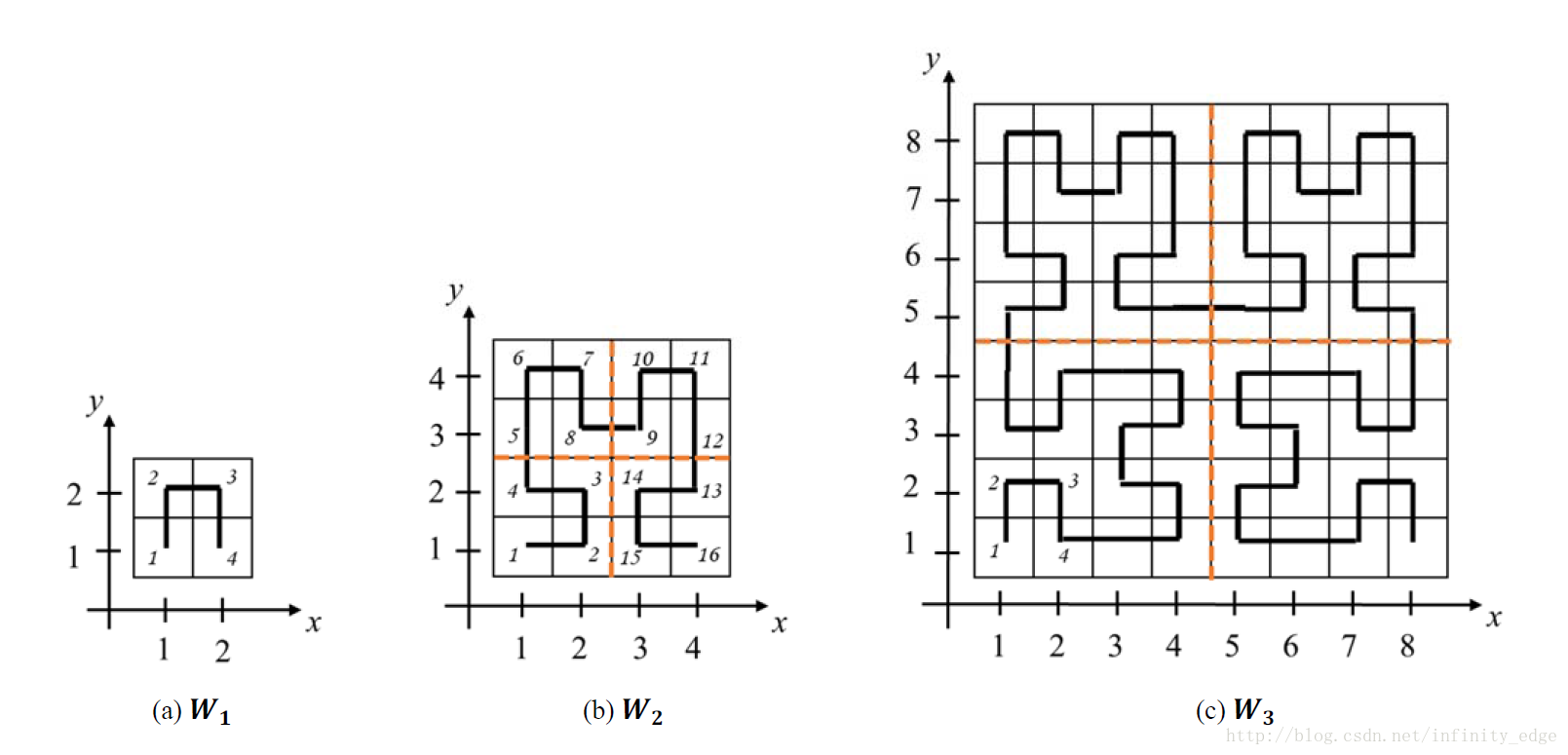
「备战PKUWC2018」2017-2018 ACM-ICPC, Asia Daejeon Regional Contest

这些题很不错，一股劣质NOIP模拟赛的味道，以后出题可以拿来用（雾）

A. Broadcast Stations

坑。

B. Connect3

题意：两个人玩在一个 $4 \times 4$ 的方格里进行的游戏。黑方先手，轮流在格子里放棋子。一个格子能被放棋子当且仅当该格下方所有格子都放满了棋子。一方获胜的条件是当且仅当存在横向，纵向或斜向的三个格子，都放着该色棋子。告诉黑方第一次放的棋子所在的列，与白方最后一次放棋子且获胜的格子的坐标，问游戏结束时合法的局面有多少种。

题解：由于有用的状态只有 $(2^5)^4 = 2^{20}$ 种，直接暴力搜索既可。代码有些恶心。

My Code：

#include
#define pi acos(-1)
#define MAXN 1048576
#define eps 1e-1using namespace std;
typedef long long ll;
typedef complex<double> E;int px, py;int vis[MAXN * 2];int ans;void dfs(int state, int cur, int x, int y){int a[4][4]; int tp[4];for(int i = 0; i < 4; i ++){int S = (state >> (i * 5)) & 31;tp[i] = 4; int tmp = 16;while(S & tmp) tp[i] --, tmp >>= 1;if(tp[i] == -1) tp[i] = 0;for(int j = 0; j < tp[i]; j ++){a[i][j] = (S >> j) & 1;}}
//                  for(int ii = 0; ii < 4; ii ++){
//                      printf("%d ", tp[ii]);
//                      for(int jj = 0; jj < tp[ii]; jj ++){
//                          printf("%d ", a[ii][jj]);
//                      }
//                      printf("\n");
//                  }
//                  printf("\n");for(int i = 0; i < 4; i ++){for(int j = 0; j < tp[i]; j ++){int flag = 1; for(int k = 0; k < 3; k ++){if(i + k >= 4){flag = 0;break;}if(tp[i + k] <= j){flag = 0;break;}if(a[i + k][j] != a[i][j]) {flag = 0;break;}}if(flag == 1){if(cur == 0 && x == px && y == py){if(vis[state]) return;vis[state] = 1;ans++;}return;}flag = 1; for(int k = 0; k < 3; k ++){if(i + k >= 4){flag = 0;break;}if(tp[i + k] <= j + k){flag = 0;break;}if(a[i + k][j + k] != a[i][j]){flag = 0;break;}}if(flag == 1){if(cur == 0 && x == px && y == py){if(vis[state]) return;vis[state] = 1;ans++;}return;}flag = 1;for(int k = 0; k < 3; k ++){if(i + k >= 4){flag = 0;break;}if(tp[i + k] <= j - k || j - k < 0){flag = 0;break;}if(a[i + k][j - k] != a[i][j]){flag = 0;break;}}if(flag == 1){if(cur == 0 && x == px && y == py){if(vis[state]) return;vis[state] = 1;ans++;}return;}flag = 1; for(int k = 0; k < 3; k ++){if(tp[i] <= j + k){flag = 0;break;}if(a[i][j + k] != a[i][j]){flag = 0;break;}}if(flag == 1){//if(state == 882230)printf("%d\n", state);if(cur == 0 && x == px && y == py){if(vis[state]) return;vis[state] = 1;ans++;}return;}}}for(int i = 0; i < 4; i ++){if(tp[i] != 4){a[i][tp[i]] = (cur ^ 1);tp[i]++;int S = state;S ^= (1 << (tp[i] + i * 5));S &= (1048575 ^ (1 << (tp[i] - 1 + i * 5)));S |= (a[i][tp[i] - 1] << (tp[i] - 1 + i * 5));dfs(S, cur ^ 1, tp[i] - 1, i);tp[i] --;//  printf("aa\n");}}
}int st;
int main(){scanf("%d%d%d", &st, &px, &py);st --; px --; py --;dfs(2 << (st * 5) ^ (1048575), 1, 0, st);printf("%d\n", ans);return 0;
}

C. Game Map

题意： $N$ 个点，$M$ 条边的无向连通图，求一个最长的序列 $\{a_k\}$，使得对于任意 $i < k$， 都有 $a_i$ 与 $a_{i + 1}$ 相邻，且与 $a_i$ 相邻的点数量严格小于与 $a_{i + 1}$ 相邻的点的数量。

$N \leq 100000, M \leq 300000$

题解：签到题之一，根据题目要求可以将原图变成 $\mathrm{DAG}$， 直接 $\mathrm{DP}$ 既可。

My Code:

#include
#define pi acos(-1)
#define MAXN 1048576
#define eps 1e-9using namespace std;
typedef long long ll;struct edge{int to, nxt;
}e[600005];int h[300005], cnt;void addedge(int x, int y){cnt++; e[cnt].to = y; e[cnt].nxt = h[x]; h[x] = cnt;cnt++; e[cnt].to = x; e[cnt].nxt = h[y]; h[y] = cnt;
}int f[300005], vis[300005];
int du[300005];
vector<int> v[300005];
int dfs(int x){if(vis[x]) return f[x];vis[x] = 1; f[x] = 1;for(int i = h[x]; i; i = e[i].nxt){if(du[e[i].to] <= du[x]) continue;f[x] = max(f[x], dfs(e[i].to) + 1);}return f[x];
}int n, m;
int main(){scanf("%d%d", &n, &m);for(int i = 1; i <= m; i ++){int x, y;scanf("%d%d", &x, &y);x++; y++;addedge(x, y);v[x].push_back(y);v[y].push_back(x);}for(int i = 1; i <= n; i ++){sort(v[i].begin(), v[i].end());for(int j = 0; j < v[i].size(); j ++){if(j == 0){du[i] ++;}else if(v[i][j] != v[i][j - 1]){du[i] ++;}}}for(int i = 1; i <= n; i ++){if(!vis[i]) dfs(i);}int ans = 0;for(int i = 1; i <= n; i ++){ans = max(ans, f[i]);}printf("%d\n", ans);return 0;
}

D. Happy Number

题意： 定义 $f(n)$ 为 $n$ 各位数字的平方和。 定义一个数 $n$ 若能经过有限步 $n \leftarrow f(n)$ 变换为 $1$ 则这个数为 $\mathrm{Happy}$ 的。给你一个数，问其是否为$\mathrm{Happy}$ 的。

题解：签到题。直接用 map 记忆化搜索一下既可。

My Code：

#include
#define pi acos(-1)
#define MAXN 1048576
#define eps 1e-9using namespace std;
typedef long long ll;
unordered_map<int, int> mp;int n;int solve(int x){if(x == 1) return 1;if(mp.count(x)) return 0;mp[x] = 1;int sum = 0;while(x){sum = sum + (x % 10) * (x % 10);x /= 10;}return solve(sum);
}int main(){scanf("%d", &n);int flag = solve(n);if(flag == 1){printf("HAPPY\n");}else{printf("UNHAPPY\n");}return 0;
}

E. How Many to Be Happy?

题意：$N$ 个点 $M$ 条边的无向图，边权互不相同。定义 $h(i)$ 为第 $i$ 条边成为最小生成树中的边最少需要删去的边的数量，求 $\sum_{i = 1}^m h(i)$ 。

$N \leq 100$ $M \leq 500$

题解：注意每条边要成为最小生成树上的边只绘删去权值比它小的边，于是对于每一条边跑一遍最小割既可。

Hash_Table’s Code：

#include
using namespace std;
const int maxn = 1009;
const int inf = 0x3f3f3f3f;int first[maxn],cur[maxn],d[maxn];
bool vis[maxn];
struct edg{int next,to,cap,flow;}e[maxn*5];
struct line{int x,y,val;}a[maxn];
int n,m,s,t,e_sum,ans;
vector<int> idx[maxn];
queue<int> q;inline int read()
{int x=0,f=1;char ch=getchar();while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}return x*f;
}
bool cmp(const line &x,const line &y){return x.valvoid add_edg(int x,int y,int z)
{e_sum++;e[e_sum].next=first[x];first[x]=e_sum;e[e_sum].to=y;e[e_sum].cap=z;e[e_sum].flow=0;
}
void insert(int x,int y,int z)
{add_edg(x,y,z);add_edg(y,x,0);
}bool bfs()
{while(!q.empty())q.pop();memset(vis,0,sizeof vis);q.push(s);vis[s]=1;d[s]=1;while(!q.empty()){int x=q.front();q.pop();for(int i=first[x];i;i=e[i].next){int w=e[i].to;if(e[i].cap>e[i].flow&&!vis[w]){q.push(w);vis[w]=1;d[w]=d[x]+1;if(w==t) return true;}}}return false;
}
int dfs(int x,int mr)
{if(x==t||mr==0) return mr;int &i=cur[x],tot=0;for(;i;i=e[i].next){int w=e[i].to;if(e[i].cap>e[i].flow&&d[w]==d[x]+1){int flow=dfs(w,min(mr,e[i].cap-e[i].flow));if(flow){tot+=flow;mr-=flow;e[i].flow+=flow;e[((i-1)^1)+1].flow-=flow;if(mr==0) return tot;}}}return tot;
}int dinic()
{int res=0;while(bfs()){for(int i=1;i<=n;i++) cur[i]=first[i];res+=dfs(s,inf);}return res;
}
int calc(int x)
{e_sum=0;memset(first,0,sizeof first);for(int i=1;i<=m;i++) if(a[x].val>a[i].val){insert(a[i].x,a[i].y,1);insert(a[i].y,a[i].x,1);}s=a[x].x;t=a[x].y;return dinic();
}int main()
{n=read();m=read();for(int i=1;i<=m;i++) a[i]=(line){read(),read(),read()},idx[a[i].val].push_back(i);sort(a+1,a+1+m,cmp);for(int i=1;i<=m;i++) ans+=calc(i);
/*  for(int i=1;i<=500;i++){int sz=idx[i].size();for(int j=0;jcout<return 0;
}

F. Philosopher’s Walk

有一个哲♂学迷宫，边长为 $2$ 的正整数次方，每个格子的长度为 $1\mathrm{m}$ ，路线如下图所示，是一个分型图：

由于迷宫有很多拐角，利于哲♂学家思♂考，因此每天都有大量哲♂学家前往，他们都是从迷宫的左下角进入。由于迷宫是未知♂领域，有不少哲♂学家在里面迷路，但是他们都能记得自己走了多少米。你需要根据哲♂学家提供的距离来判断哲♂学家所处的坐标，从而驾驶直升机将其解♂救出来。

迷宫边长 $\leq 2^{15}$ 。

题解：签到题。根据走的步数判断在四个小区域中的哪一个，然后递归实现。

My Code：

#include
#define pi acos(-1)
#define MAXN 1048576
#define eps 1e-9using namespace std;
typedef long long ll;
typedef pair<int, int> P;P solve(int n, int m){if(n == 2){if(m == 0) return make_pair(1, 1);if(m == 1) return make_pair(1, 2);if(m == 2) return make_pair(2, 2);if(m == 3) return make_pair(2, 1);}int k = n / 2;int t1 = m / (k * k);if(t1 == 0){P tmp = solve(n >> 1, m % (k * k));swap(tmp.first, tmp.second);return tmp;}if(t1 == 1){P tmp = solve(n >> 1, m % (k * k));tmp.second += k;return tmp;}if(t1 == 2){P tmp = solve(n >> 1, m % (k * k));tmp.first += k; tmp.second += k;return tmp;}if(t1 == 3){P tmp = solve(n >> 1, m % (k * k));P ret;ret.first = k - tmp.second + 1;ret.second = k - tmp.first + 1;ret.first += k;return ret;}
}int n, m;
int main(){scanf("%d%d", &n, &m);m--;P tmp = solve(n, m);printf("%d %d\n", tmp.first, tmp.second);return 0;
}

G. Rectilinear Regions

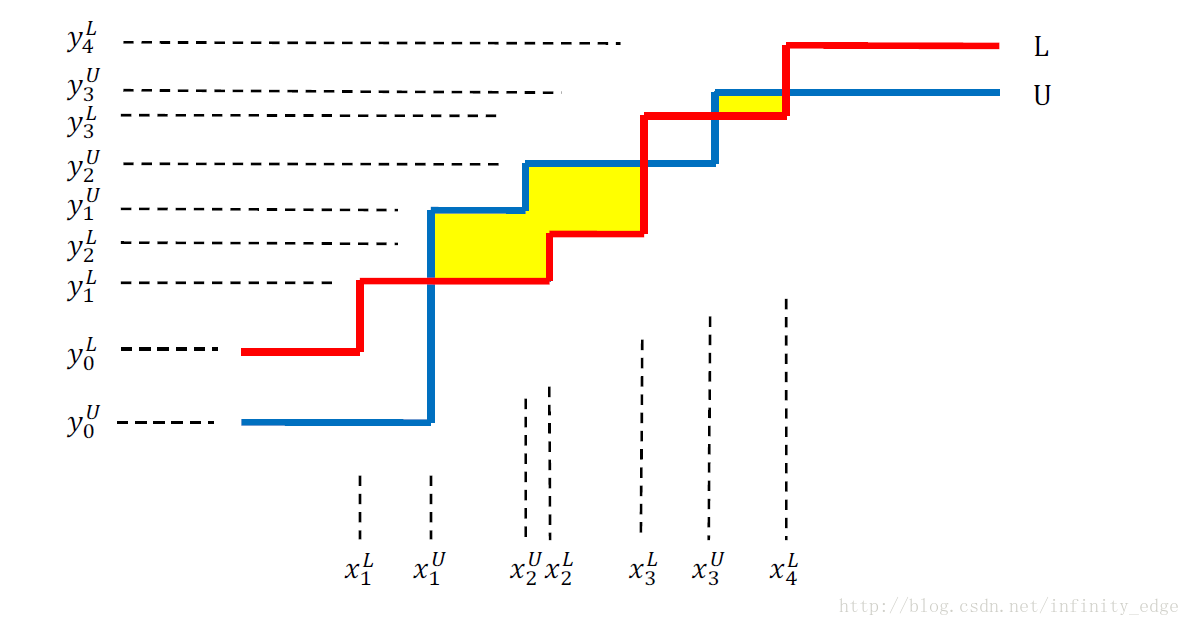
题意：有两条阶梯形线（一红一蓝），求红线与蓝线所围成的封闭图形且红线在下（如图中的黄色区域）的个数与面积和。

折点数 $\leq 25000$ 。

题解：如果两条线的单调性不同，答案为 $0$， 若都是单调递减，将纵坐标取反后交换两条直线。就变成了都是单调递增的情况。
这时我们按照折点的横坐标排一遍序，扫一遍统计答案既可。

My Code：

#include
#define pi acos(-1)
#define MAXN 1048576
#define eps 1e-1using namespace std;
typedef long long ll;
typedef complex<double> E;struct node {int x, y, id;
} a[100005], b[100005], c[200005];
int cmp(node a, node b){return a.x < b.x;
}
int n, m;
int dy0, dy1;
int main() {scanf("%d%d", &n, &m);scanf("%d", &dy0);for(int i = 1; i <= n; i ++) {scanf("%d%d", &a[i].x, &a[i].y);a[i].id = 0;}scanf("%d", &dy1);for(int i = 1; i <= m; i ++) {scanf("%d%d", &b[i].x, &b[i].y);b[i].id = 1;}int d0 = a[1].y > dy0;int d1 = b[1].y > dy1;if(d0 != d1) {printf("0 0\n");return 0;}if(d1 == 0) {dy0 *= -1;dy1 *= -1;for(int i = 1; i <= n; i ++) {a[i].y = -a[i].y;a[i].id = 1;}for(int i = 1; i <= m; i ++) {b[i].y = -b[i].y;b[i].id = 0;}swap(dy0, dy1);swap(a, b);swap(n, m);}for(int i = 1; i <= n; i ++) {c[i] = a[i];}for(int i = 1; i <= m; i ++) {c[n + i] = b[i];}sort(c + 1, c + n + m + 1, cmp);int cnt = 0;ll ans = 0;ll tmp = 0;int lst = -1;bool flag = dy1 > dy0;for(int i = 1; i <= n + m; i ++) {if(c[i].id == 0) {if(lst != -1) {tmp = tmp + 1ll * (c[i].x - lst) * (dy1 - dy0);if (c[i].y < dy1) lst = c[i].x;else lst = -1, ++cnt, ans += tmp, tmp = 0;}dy0 = c[i].y;if (dy0 >= dy1) flag = false;}else{if(lst != -1) {tmp = tmp + 1ll * (c[i].x - lst) * (dy1 - dy0);lst = c[i].x;}dy1 = c[i].y;if (!flag && lst == -1 && dy1 > dy0) {lst = c[i].x;}}}printf("%d %I64d\n", cnt, ans);return 0;
}

H. Rock Paper Scissors

题意：你和电脑玩剪刀石头布，给出电脑和你的出拳序列（长度分别为 $n, m$ 且 $m \leq n$）。你需要找到一个开始的位置 $pos$ ，从 $pos$ 开始进行游戏，比较 $a[pos + i]$ 与 $b[i]$ （$a[]$ 为电脑的出拳序列，$b[]$ 为你的出拳序列），直到一方的出拳序列结束为止。问你最多能够赢几局。

$1 \leq m \leq n \leq 10^5$

题解：枚举你出的每一种拳，将其设为 $1$， 其他的设为 $0$ ，将电脑序列中你能赢的拳设为 $1$， 其他的设为 $0$ ，则对于每一个pos，只比较你的该种出拳能够胜利的局数为

My Code：

#include
#define pi acos(-1)
#define MAXN 1048576
#define eps 1e-1using namespace std;
typedef long long ll;
typedef complex<double> E;void bit_reverse(int N, E *r){for(int i = 0, j = 0; i < N; i ++){if(i > j) swap(r[i], r[j]);for(int l = N >> 1; (j ^= l) < l; l >>= 1);}
}void fft(E *r, int N, int f){bit_reverse(N, r);for(int i = 2; i <= N; i <<= 1){int m = i >> 1;for(int j = 0; j < N; j += i){E w(1, 0); E wn(cos(2 * pi / i), f * sin(2 * pi / i));for(int k = 0; k < m; k ++){E z = r[j + k + m] * w;r[j + k + m] = r[j + k] - z;r[j + k] = r[j + k] + z;w *= wn;}}}if(f == -1){for(int i = 0; i < N; i ++) r[i] /= N;}
}
E a[MAXN], b[MAXN];
int ans1[MAXN], ans2[MAXN], ans3[MAXN];
int m, n, N;
char S1[300005], S2[300005];
int s1[300005], s2[300005];int main(){scanf("%d%d", &n, &m);N = 1;while(N <= (m + n + m)) N <<= 1;scanf("%s", S2 + 1);scanf("%s", S1 + 1);for(int i = 1; i <= m / 2; i ++){swap(S1[i], S1[m - i + 1]);}for(int i = 1; i <= m; i ++){if(S1[i] == 'R') s1[i] = 1;else s1[i] = 0;}for(int i = 1; i <= n; i ++){if(S2[i] == 'S') s2[i] = 1;else s2[i] = 0;}for(int i = 0; i < N; i ++) a[i] = b[i] = 0;for(int i = 1; i <= m; i ++){a[i - 1] = 1ll * s1[i];}for(int i = 1; i <= n; i ++){b[i - 1] = 1ll * s2[i];}fft(a, N, 1); fft(b, N, 1);for(int i = 0; i < N; i ++) a[i] *= b[i];fft(a, N, -1);for(int i = m; i <= n + m - 1; i ++){ans1[i - m + 1] += int(a[i - 1].real() + 0.01);}for(int i = 1; i <= m; i ++){if(S1[i] == 'S') s1[i] = 1;else s1[i] = 0;}for(int i = 1; i <= n; i ++){if(S2[i] == 'P') s2[i] = 1;else s2[i] = 0;}for(int i = 0; i < N; i ++) a[i] = b[i] = 0;for(int i = 1; i <= m; i ++){a[i - 1] = 1ll * s1[i];}for(int i = 1; i <= n; i ++){b[i - 1] = 1ll * s2[i];}fft(a, N, 1); fft(b, N, 1);for(int i = 0; i < N; i ++) a[i] *= b[i];fft(a, N, -1);for(int i = m; i <= n + m - 1; i ++){ans2[i - m + 1] += int(a[i - 1].real() + 0.01);}for(int i = 1; i <= m; i ++){if(S1[i] == 'P') s1[i] = 1;else s1[i] = 0;}for(int i = 1; i <= n; i ++){if(S2[i] == 'R') s2[i] = 1;else s2[i] = 0;}for(int i = 0; i < N; i ++) a[i] = b[i] = 0;for(int i = 1; i <= m; i ++){a[i - 1] = 1ll * s1[i];}for(int i = 1; i <= n; i ++){b[i - 1] = 1ll * s2[i];}fft(a, N, 1); fft(b, N, 1);for(int i = 0; i < N; i ++) a[i] *= b[i];fft(a, N, -1);for(int i = m; i <= n + m - 1; i ++){ans3[i - m + 1] += int(a[i - 1].real() + 0.01);}int tot = 0;for(int i = 1; i <= n; i ++){tot = max(tot, ans1[i] + ans2[i] + ans3[i]);}printf("%d\n", tot);return 0;
}

I. Slot Machines

题意：有一种老虎机，每次玩都绘在 $0 \sim 999999$ 中随机生成一个数。由于这种老虎机过于落后，生成的是一个伪随机数，即存在数 $p, k$ 使得对于任何 $i > k$，都有 $a_{i + p} = a_i$
即 $p$ 为循环节，$k$ 为循环起始位置。
为了拿到大奖，你现在得到了该老虎机的一部分随机数序列，准备分析它最可能的循环节。最可能循环节的 $p + k$ 最小，求最可能的循环节的 $p$ 与 $k$ 。

题解：我们把序列反过来，求出它的 $\mathrm{next}$ 数组。可以证明前 $n$ 个数的最短循环节为 $i - next[i]$ 。然后枚举每个位置更新答案即可。

My Code

#include
#define pi acos(-1)
#define MAXN 1048576
#define eps 1e-9using namespace std;
typedef long long ll;
typedef pair<int, int> P;int nxt[1000005];
int a[1000005];
int b[1000005];
int n, m;
int main(){scanf("%d", &n);for(int i = 1; i <= n; i ++) scanf("%d", &a[i]);for(int i = 1; i <= n; i ++) b[n - i + 1] = a[i];nxt[1] = 0;for(int i = 1; i < n; i ++){int j = nxt[i];while(j && b[j + 1] != b[i + 1]) j = nxt[j];nxt[i + 1] = (b[j + 1] == b[i + 1]) ? j + 1 : 0;}int ans = 0x3f3f3f3f, p = 0, k = 0;for(int i = 1; i <= n; i ++){int np = (n - i + 1 - nxt[n - i + 1]);if(i + np < ans || (i + np == ans && np < p)){ans = i + np;k = i - 1; p = np;}}printf("%d %d\n", k, p);return 0;
}

J. Strongly Matchable

坑。

K. Untangling Chain

题意：平面直角坐标系中有一个拐点数为 $n$ 的折线，每条边均与坐标轴平行。现在你需要修改每条边的长度（但方向不能改变），使得所有边之间除了相邻边的公共端点之外没有交点，要求每条边的长度不超过 $n$。

$n \leq 10000$

题解：我们记录一下当前折线覆盖的横纵坐标的最小值与最大值，贪心得使该边的长度恰好将该边的另一个端点越过当前横（纵）坐标的最小（最大）值，这样由于只有 $90°$ 转弯，下一条边就一定不会与之前的边冲突。

My Code：

#include
#define pi acos(-1)
#define MAXN 1048576
#define eps 1e-1using namespace std;
typedef long long ll;
typedef complex<double> E;const int dx[] = {0, 1, 0, -1};
const int dy[] = {1, 0, -1, 0};int a[100005], d[100005];
int n;
int main(){scanf("%d", &n);for(int i = 1; i <= n; i ++){scanf("%d%d", &a[i], &d[i]);    }int di = 0;int minx = 0, maxx = 0, miny = 0, maxy = 0;int px = 0, py = 0;for(int i = 1; i <= n; i ++){if(di == 0){a[i] = maxx + 1 - px;px += a[i];maxx = max(maxx, px);}if(di == 1){a[i] = maxy + 1 - py;py += a[i];maxy = max(maxy, py);}if(di == 2){a[i] = px - minx + 1;px -= a[i];minx = min(minx, px);}if(di == 3){a[i] = py - miny + 1;py -= a[i];miny = min(miny, py);}di = (di + d[i] + 4) % 4;}for(int i = 1; i <= n; i ++){printf("%d ", a[i]);    }return 0;
}

L. Vacation Plans

坑。

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！