常用的数据结构以及常用的算法
常用的数据结构以及常用的算法
常用数据结构
数据结构是计算机存储、组织数据的方式。
数据结构是指相互之间存在一种或多种特定关系的数据元素的集合。
通常情况下,精心选择的数据结构可以带来更高的运行或者存储效率。
数据结构往往同高效的检索算法和索引技术有关。
一、线性表
线性结构: 最常用、最简单的一种数据结构。
线性表: 典型的线性结构。基本特点是线性表中的
数据元素有序且有限。结构中:
① 存在一个唯一的被称为“第一个”的数据元素;
② 存在一个唯一的被称为“最后一个”的数据元素;
③ 除第一个元素外,每个元素均有唯一一个直接前驱;
④ 除最后一个元素外,每个元素均有唯一一个直接后继
线性表按存储方式可分为顺序表和链表。
线性表的基本运算是指对线性表的操作,常见的包括:求长度、置空表、遍历、查找、修改、删除、插入、排序等。
此外还有复杂的运算,比如线性表的合并、反转、求中值、删除重复元素等。
链表包括单链表、循环链表、双向链表和静态链表等。
链表采用动态存储分配方式,需要时申请,不需要时释放。
操作时间复杂度:插入、删除O(1),查询、修改、遍历、求长度O(n)。
空间性能方面,顺序表的存储空间是静态分配的,需提前确定其大小,更改的话容易造成浪费。
适用于存储规模确定,不经常变更或变更不大的场合;动态链表是动态分配空间的,不容易溢出。适用于长度变化大的场合。但由于要存储指针,故空间利用率较低。
二、栈和队列
栈(Stack):是限制在表的一端进行插入和删除操作的线性表。
又称为后进先出LIFO (Last In First Out)或先进后出FILO (First In Last Out)线性表。
栈顶(Top):允许进行插入、删除操作的一端,又称为表尾。
用栈顶指针(top)来指示栈顶元素。
栈底(Bottom,Base):是固定端,又称为表头。
空栈:当表中没有元素时称为空栈。
设栈S=(a1,a2,…an),则a1称为栈底元素,an为栈顶元素,如图所示。 栈中元素按a1,a2,…an的次序进栈,退栈的第一个元素应为栈顶元素。即栈的修改是按后进先出的原则进行的。

队列(Queue):也是运算受限的线性表。
是一种先进先出(First In First Out ,简称FIFO)的线性表。
只允许在表的一端进行插入,而在另一端进行删除。
队首(front) :允许进行删除的一端称为队首。
队尾(rear) :允许进行插入的一端称为队尾。
队列中没有元素时称为空队列。在空队列中依次加入元素a1, a2, …, an之后,a1是队首元素,an是队尾元素。显然退出队列的次序也只能是a1, a2, …, an ,即队列的修改是依先进先出的原则进行的,如图所示。

三、数和二叉树
树(Tree)是n(n≧0)个结点的有限集合T,若n=0时称为空树,否则非空树:
⑴有且只有一个特殊的称为树的根(Root)结点;
⑵ 若n>1时,其余的结点被分为m(m>0)个互不相交的子集T1, T2, …Tm,其中每个子集本身又是一棵树,称其为根的子树(Subtree)。
二叉树(Binary tree):
(1)每个结点至多只有两棵子树(即二叉树中不存在度大于2的结点) (2)子树有序(有左右之分),次序不能颠倒
二叉树非常重要。
(1)结构简单,存储效率高
(2)操作算法相对简单,任何树都很容易转化成二叉树结构。
树的结构十分直观,而树的很多概念定义都有一个相同的特点:
递归,也就是说,一棵树要满足某种性质,往往要求每个节点都必须满足。
例如,在定义一棵二叉搜索树时,每个节点也都必须是一棵二叉搜索树。
正因为树有这样的性质,大部分关于树的面试题都与递归有关,换句话说,面试官希望通过一道关于树的问题来考察你对于递归算法掌握的熟练程度。
树的形状:在面试中常考的树的形状有:普通二叉树、平衡二叉树、完全二叉树、二叉搜索树、四叉树(Quadtree)、多叉树(N-ary Tree)。
四、图
图(Graph)是一种比线性表和树更为复杂的数据结构。线性结构:是研究数据元素之间的一对一关系。在这种结构中,除第一个和最后一个元素外,任何一个元素都有唯一的一个直接前驱和直接后继。
树结构:是研究数据元素之间的一对多的关系。
在这种结构中,每个元素对下(层)可以有0个或多个元素相联系,对上(层)只有唯一的一个元素相关,数据元素之间有明显的层次关系。
图结构:是研究数据元素之间的多对多的关系。在这种结构中,任意两个元素之间可能存在关系。即结点之间的关系可以是任意的,图中任意元素之间都可能相关。
一个图(G)定义为一个偶对(V,E) ,记为G=(V,E) 。其中: V是顶点(Vertex)的非空有限集合,记为V(G);E为两个顶点间的关系集合,记为E(G) ,其元素是图的弧(Arc)或者边 (Edge)
常用算法
算法(Algorithm)是指解题方案的准确而完整的描述。
是一系列解决问题的清晰指令,算法代表着用系统的方法描述解决问题的策略机制。
也就是说,能够对一定规范的输入,在有限时间内获得所要求的输出。
如果一个算法有缺陷,或不适合于某个问题,执行这个算法将不会解决这个问题。
不同的算法可能用不同的时间、空间或效率来完成同样的任务。
一个算法的优劣可以用空间复杂度与时间复杂度来衡量。
| 排序方法 | 时间复杂度 |
|---|---|
| 直接插入排序 | O(n²) |
| 希尔排序 | O(n㏒2n) |
| 冒泡排序 | O(n²) |
| 快速排序 | O(n㏒2n) |
| 直接选择排序 | O(n²) |
一、直接插入排序
1、排序思想
将待排序的记录Ri,插入到已排好序的记录表R1, R2,…., Ri-1中,得到一个新的、记录数增加1的有序表。 直到所有的记录都插入完为止。
设待排序的记录顺序存放在数组R[1…n]中,在排序的某一时刻,将记录序列分成两部分:
◆ R[1…i-1]:已排好序的有序部分;
◆ R[i…n]:未排好序的无序部分。
显然,在刚开始排序时,R[1]是已经排好序的。
例:设有关键字序列为:7, 4, -2, 19, 13, 6,直接插入排序的过程如图所示:

2、算法实现
void straight_insert_sort(Sqlist *L){int i, j ;for (i=2; i<=L->length; i++){L->R[0]=L->R[i]; j=i-1; /* 设置哨兵 */while( LT(L->R[0].key, L->R[j].key) ){L->R[j+1]=L->R[j];j--;} /* 查找插入位置 */ L->R[j+1]=L->R[0]; /* 插入到相应位置 */ }}
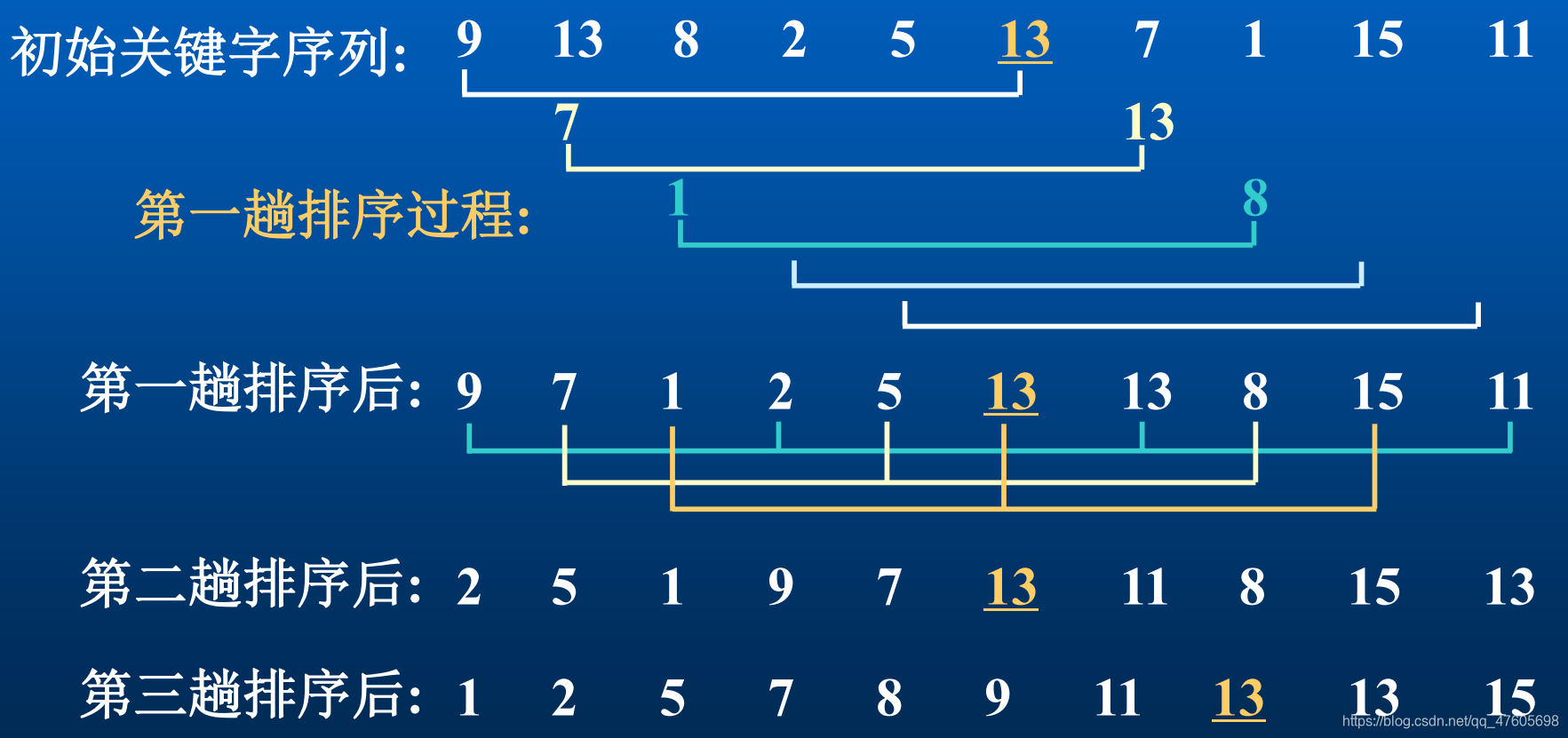
二、希尔排序
1、排序思想
① 先取一个正整数d1(d1
2、算法实现
先给出一趟希尔排序的算法,类似直接插入排序。
void shell_pass(Sqlist *L, int d){
/* 对顺序表L进行一趟希尔排序, 增量为d */int j, k ;for (j=d+1; j<=L->length; j++){ L->R[0]=L->R[j] ; /* 设置监视哨兵 */k=j-d ;while (k>0&<(L->R[0].key, L->R[k].key) ){L->R[k+d]=L->R[k] ; k=k-d ; }L->R[k+j]=L->R[0] ;}
}
然后在根据增量数组dk进行希尔排序。
void shell_sort(Sqlist *L, int dk[], int t)/* 按增量序列dk[0 … t-1],对顺序表L进行希尔排序 */
{ int m ;for (m=0; m<=t; m++)shll_pass(L, dk[m]) ;
}
三、冒泡排序
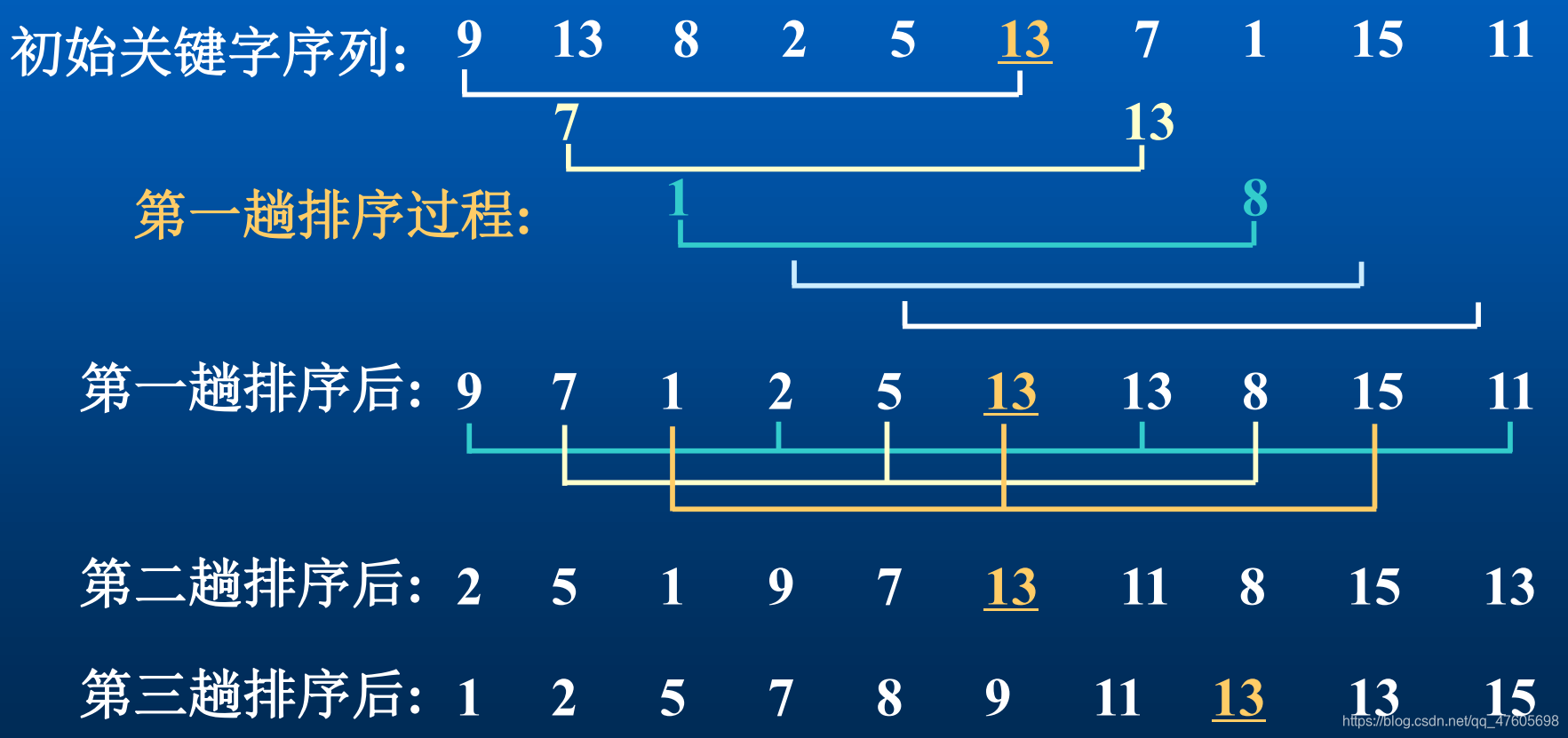
1、算法思想
依次比较相邻的两个记录的关键字,若两个记录是反序的(即前一个记录的关键字大于后前一个记录的关键字),则进行交换,直到没有反序的记录为止。 ① 首先将L->R[1]与L->R[2]的关键字进行比较,若为反序(L->R[1]的关键字大于L->R[2]的关键字),则交换两个记录;然后比较L->R[2]与L->R[3]的关键字,依此类推,直到L->R[n-1]与 L->R[n]的关键字比较后为止,称为一趟冒泡排序, L->R[n]为关键字最大的记录。
② 然后进行第二趟冒泡排序,对前n-1个记录进行同样的操作。 一般地,第i趟冒泡排序是对L->R[1 … n-i+1]中的记录进行的,因此,若待排序的记录有n个,则要经过n-1趟冒泡排序才能使所有的记录有序。
设有9个待排序的记录,关键字分别为23, 38, 22, 45, 23, 67, 31, 15, 41,冒泡排序的过程如图所示。
2、算法实现
#define FALSE 0
#define TRUE 1
void Bubble_Sort(Sqlist *L){int j ,k , flag ;for (j=0; j<L->length; j++){/* 共有n-1趟排序 */flag=TRUE ;for (k=1; k<=L->length-j; k++) /* 一趟排序 */if (LT(L->R[k+1].key, L->R[k].key ) ){flag=FALSE ; L->R[0]=L->R[k] ; L->R[k]=L->R[k+1] ; L->R[k+1]=L->R[0] ; }if (flag==TRUE) break ;}
}
四、快速排序
1、算法思想
通过一趟排序,将待排序记录分割成独立的两部分,其中一部分记录的关键字均比另一部分记录的关键字小,再分别对这两部分记录进行下一趟排序,以达到整个序列有序。
设待排序的记录序列是R[s…t] ,在记录序列中任取一个记录(一般取R[s])作为参照(又称为基准或枢 轴),以R[s].key为基准重新排列其余的所有记录,
方法是:
◆ 所有关键字比基准小的放R[s]之前;
◆ 所有关键字比基准大的放R[s]之后。
以R[s].key最后所在位置i作为分界,将序列R[s…t]分割成两个子序列,称为一趟快速排序。
设有6个待排序的记录,关键字分别为29, 38, 22, 45, 23, 67,一趟快速排序的过程如图所示。

2、算法实现
递归算法
void quick_Sort(Sqlist *L , int low, int high){int k ;if (low<high) {k=quick_one_pass(L, low, high);quick_Sort(L, low, k-1);quick_Sort(L, k+1, high);} /* 序列分为两部分后分别对每个子序列排序
}
非递归算法
# define MAX_STACK 100
void quick_Sort(Sqlist *L , int low, int high){int k , stack[MAX_STACK] , top=0; do {while (low<high){k=quick_one_pass(L,low,high); stack[++top]=high ; stack[++top]=k+1 ;/* 第二个子序列的上,下界分别入栈 */high=k-1 ; }if (top!=0) {low=stack[top--] ; high=stack[top--] ; }}while (top!=0&&low<high) ;
}
五、简单选择排序
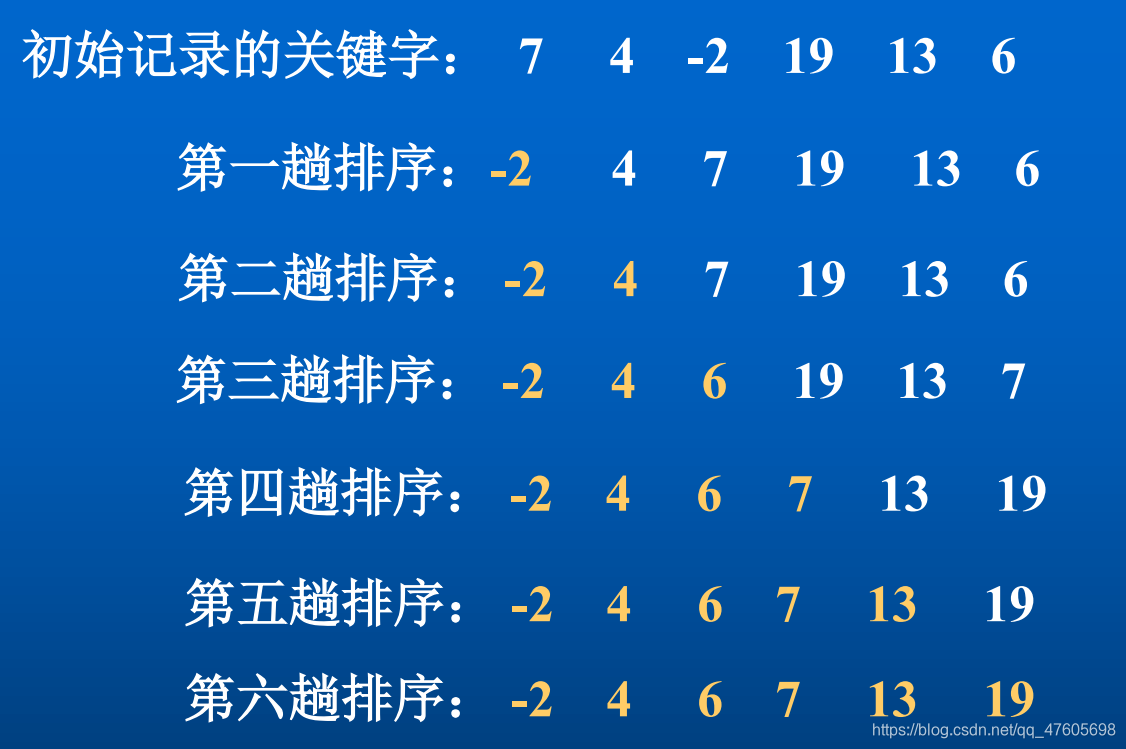
1、算法思想
简单选择排序(Simple Selection Sort ,又称为直接选择排序)的基本操作是:通过n-i次关键字间的比较,从n-i+1个记录中选取关键字最小的记录,然后和第i个记录进行交换,i=1, 2, … n-1 。
例:设有关键字序列为:7, 4, -2, 19, 13, 6,直接选择排序的过程如下图所示。
2、算法实现
void simple_selection_sort(Sqlist *L){int m, n , k;for (m=1; m<L->length; m++){k=m ; for (n=m+1; n<=L->length; n++)if ( LT(L->R[n].key, L->R[k].key) ) k=n ;if (k!=m) /* 记录交换 */{L->R[0]=L->R[m]; L->R[m]=L->R[k];L->R[k]=L->R[0];} } }
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!