机器学习：线性判别分析从理论到公式推导（LDA）

机器学习：线性判别分析从理论到公式推导（LDA）

• 数据定义
• 理论概述与变量定义
• 公式推导

数据定义

DataSet X：= ( x i , y i ) i = 1 N , 令 X 的每个观测值 x i ∈ R p {(x_i,y_i)}_{i=1}^N,令X的每个观测值xi \in R^p (xi​,yi​)i=1N​,令X的每个观测值xi∈Rp，Y的每个元素 y i ∈ R y_i\in R yi​∈R，我们继续化简，X= [ x 11 x 12 . . . x 1 p x 21 x 22 . . . x 2 p . . . . . . x n 1 x n 2 . . . x n p ] (1) \left[ \begin{matrix} x_{11} & x_{12} &... x_{1p} \\ x_{21} & x_{22} &... x_{2p} \\ \\...... \\x_{n1} & x_{n2} &... x_{_{np}} \end{matrix} \right]\tag{1} ⎣ ⎡​x11​x21​......xn1​​x12​x22​xn2​​...x1p​...x2p​...xnp​​​⎦ ⎤​(1)
Y= [ y 1 y 2 . . . . . . y n ] (2) \left[ \begin{matrix} y_{1} \\ y_{2} \\ \\...... \\y_n \end{matrix} \right]\tag{2} ⎣ ⎡​y1​y2​......yn​​⎦ ⎤​(2)
其中 y i 为 + 1 的输入 C 1 类别， y i 为 − 1 的输入 C 2 y_i为+1的输入C1类别，y_i为-1的输入C2 yi​为+1的输入C1类别，yi​为−1的输入C2类别。 X c 1 = ( x i ∣ y i = + 1 ) X_c1=(x_i|y_i=+1) Xc​1=(xi​∣yi​=+1) X c 2 = ( x i ∣ y i = − 1 ) Xc2=(x_i|y_i=-1) Xc2=(xi​∣yi​=−1)

理论概述与变量定义

为了方便可视化，我们先令数据集的维度p=1，也就是每个观测值 x i x_i xi​的维度为1。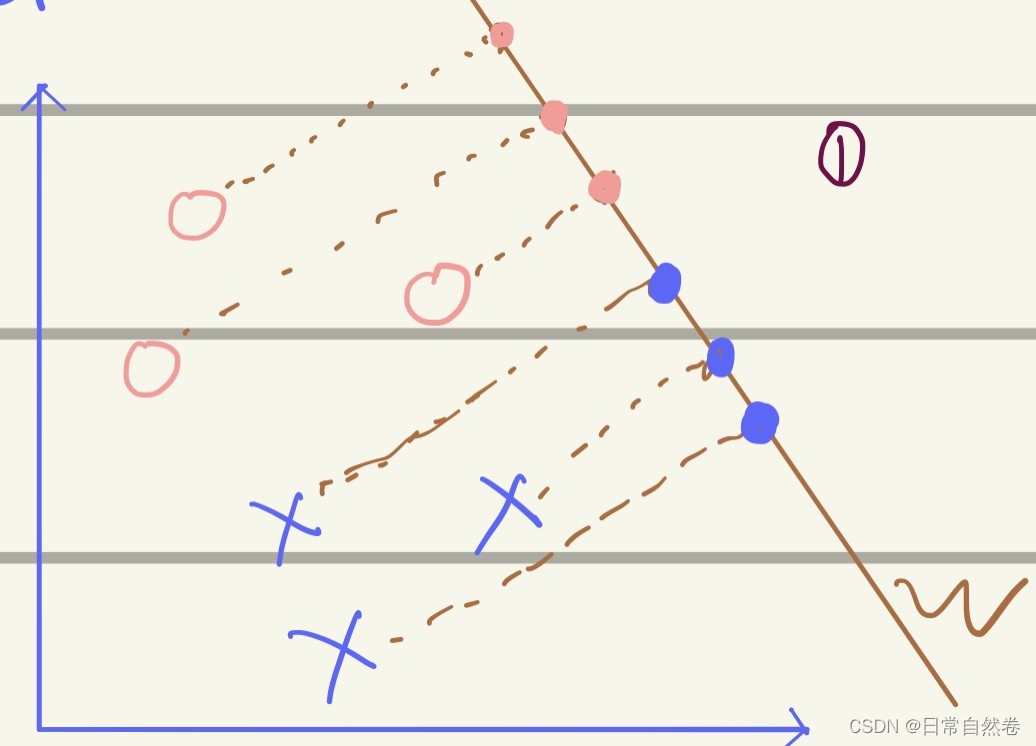
从图中我们可以看到，把这些坐标点投影到一维直线w上，可以发现，当观测值 x i x_i xi​如果投影到了一个合适的Vector上，就会很容易的在Vector上找到一个threshold（阈值），把⭕️与❌分开，但是如果，没有找到一个很好的Vector，就会像下面这幅图：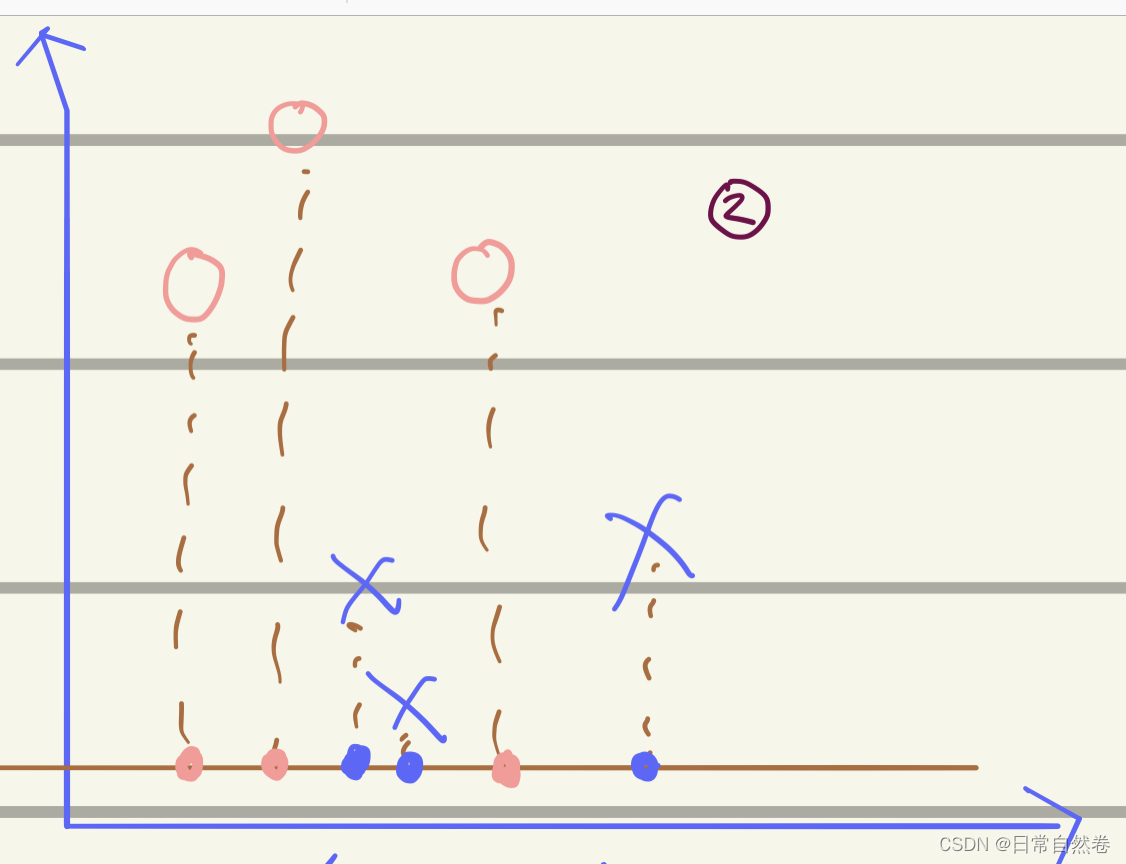
我们会发现，这两类数据交替出现，不能找一个一个合适的阈值将这两类数据分开。，所以我们要是想把这些数据分开就需要找到一个合适的Vector的方向。
我们通过观察投影到Vector w上面的坐标，我们发现当两类数据的距离越大分类效果越好，每一个分类内之间的数据约紧凑越好。也就是我们要找到一个Vector可以让投影在Vector 上的数据实现：类内小，类间大，还有一种解释：高内聚，松耦合，我起初听到这几句话的时候，感觉特别晦涩难懂，我们通过数学的口吻来解释：
类内小：也就是一个类别的观测值的在Vector上面的投影值之间方差足够小。
类间大：也就是说两个类别的观测值的在Vector上面的投影值的均值差距足够大。
我们现在已经有数据了，那么我们可以通过这个条件来反推出Vector的方向。
下面我们用公式表示：
观测值在Vector上面的投影可以表示为： z i = w T x i z_i=w^Tx_i zi​=wTxi​,这里我们假设Vector的模$｜w｜$的值为1（因为我们主要关心的是Vector的方向，长度是可以自由伸缩的）

公式推导

x i 与 w 的点乘表示为： ∣ x i ∣ ∗ ∣ w ∣ ∗ c o s θ , 因为 ∣ w ∣ = 1 , 所以 x i ⋅ w = ∣ x i ∣ ⋅ c o s θ x_i与w的点乘表示为：|x_i|*|w|*cos\theta,因为|w|=1,所以x_i\cdot w =|x_i|\cdot cos\theta xi​与w的点乘表示为：∣xi​∣∗∣w∣∗cosθ,因为∣w∣=1,所以xi​⋅w=∣xi​∣⋅cosθ
均值： 1 N ∑ i = 1 N x i = z i \frac{1}{N} \sum_{i=1}^Nx_i=z_i N1​∑i=1N​xi​=zi​
方差： 1 N ∑ i = 1 N ( x i − z i ) ( x i − z i ) T \frac{1}{N}\sum_{i=1}^{N}(x_i-z_i)(x_i-z_i)^T N1​∑i=1N​(xi​−zi​)(xi​−zi​)T
C1：
均值： 1 N 1 ∑ i = 1 N 1 x i = z i \frac{1}{N_1} \sum_{i=1}^{N_1}x_i=z_i N1​1​∑i=1N1​​xi​=zi​
方差： 1 N 1 ∑ i = 1 N 1 ( x i − z i ) ( x i − z i ) T = s 1 \frac{1}{N_1}\sum_{i=1}^{{N_1}}(x_i-z_i)(x_i-z_i)^T=s_1 N1​1​∑i=1N1​​(xi​−zi​)(xi​−zi​)T=s1​
C2：
均值： 1 N 2 ∑ i = 1 N 2 x i = z i \frac{1}{N_2} \sum_{i=1}^{N_2}x_i=z_i N2​1​∑i=1N2​​xi​=zi​
方差： 1 N 2 ∑ i = 1 N 2 ( x i − z i ) ( x i − z i ) T = s 2 \frac{1}{N_2}\sum_{i=1}^{{N_2}}(x_i-z_i)(x_i-z_i)^T=s_2 N2​1​∑i=1N2​​(xi​−zi​)(xi​−zi​)T=s2​

类间： ( z 1 − z 2 ) 2 (z_1-z_2)^2 (z1​−z2​)2
类内： s 1 + s 2 s_1+s_2 s1​+s2​
为了让类内小，类间大，
目标函数 J ( w ) = ( z 1 − z 2 ) 2 s 1 + s 2 J(w)=\frac{(z_1-z_2)^2}{s_1+s_2} J(w)=s1​+s2​(z1​−z2​)2​
化简分子：
( z 1 − z 2 ) 2 = ( 1 N 1 ∑ i = 1 N w t x i − 1 N 2 ∑ i = 1 N w t x i ) 2 (z_1-z_2)^2 = (\frac{1}{N_1}\sum_{i=1}^Nw^tx_i-\frac{1}{N_2}\sum_{i=1}^Nw^tx_i)^2 (z1​−z2​)2=(N1​1​∑i=1N​wtxi​−N2​1​∑i=1N​wtxi​)2
= ( w t ( 1 N 1 ∑ i = 1 N x i − 1 N 2 ∑ i = 1 N x i ) ) ) 2 =(w^t(\frac{1}{N_1}\sum_{i=1}^Nx_i-\frac{1}{N_2}\sum_{i=1}^Nx_i)))^2 =(wt(N1​1​∑i=1N​xi​−N2​1​∑i=1N​xi​)))2
= ( w t ( x 1 ‾ − x 2 ‾ ) ) 2 =(w^t(\overline{x_1}-\overline{x_2}))^2 =(wt(x1​​−x2​​))2
= w t ( x 1 ‾ − x 2 ‾ ) ( x 1 ‾ − x 2 ‾ ) T w =w^t(\overline{x_1}-\overline{x_2})(\overline{x_1}-\overline{x_2})^Tw =wt(x1​​−x2​​)(x1​​−x2​​)Tw

s 1 + s 2 = 1 N 1 ∑ i = 1 N ( z i − z c 1 ‾ ) ( z i − z c 1 ‾ ) T + 1 N 2 ∑ i = 1 N ( z i − z c 2 ‾ ) ( z i − z c 2 ‾ ) T s_1+s_2=\frac{1}{N_1}\sum_{i=1}^N(z_i-\overline{z_{c1}})(z_i-\overline{z_{c1}})^T+\frac{1}{N_2}\sum_{i=1}^N(z_i-\overline{z_{c2}})(z_i-\overline{z_{c2}})^T s1​+s2​=N1​1​∑i=1N​(zi​−zc1​​)(zi​−zc1​​)T+N2​1​∑i=1N​(zi​−zc2​​)(zi​−zc2​​)T
提取w，最终化简结果
= w T ( s c 1 + s c 2 ) w =w^T(s_{c1}+s_{c2})w =wT(sc1​+sc2​)w
J ( w ) = w t ( x 1 ‾ − x 2 ‾ ) ( x 1 ‾ − x 2 ‾ ) T w w T ( s c 1 + s c 2 ) w J(w)=\frac{w^t(\overline{x_1}-\overline{x_2})(\overline{x_1}-\overline{x_2})^Tw}{w^T(s_{c1}+s_{c2})w} J(w)=wT(sc1​+sc2​)wwt(x1​​−x2​​)(x1​​−x2​​)Tw​
我们令类间方差差 s b = ( x 1 ‾ − x 2 ‾ ) ( x 1 ‾ − x 2 ‾ ) s_b=(\overline{x_1}-\overline{x_2})(\overline{x_1}-\overline{x_2}) sb​=(x1​​−x2​​)(x1​​−x2​​)

令类内方差： s w = s c 1 + s c 2 s_w=s_{c1}+s_{c2} sw​=sc1​+sc2​
所以 J ( w ) = w T s w w w T s b w J(w)=\frac{w^Ts_ww}{w^Ts_bw} J(w)=wTsb​wwTsw​w​
我们对目标函数求偏导数，令其等于0.最终得到：
w = w T S w w w T s b w s w − 1 s b w w=\frac{w^TS_ww}{w^Ts_bw}s_w^{-1}s_bw w=wTsb​wwTSw​w​sw−1​sb​w
由上面推到中可知：$w的size为1\ast ps的size为p\ast$，所以 w T S w w w^TS_ww wTSw​w与 w T s b w w^Ts_bw wTsb​w为一维常数，
由于我们最终需要求的是Vector 的方向，所以我们约去与方向无关的变量。
w 正比于 s w − 1 ( x 1 ‾ − x 2 ‾ ) w正比于s_w^{-1}(\overline{x_1}-\overline{x_2}) w正比于sw−1​(x1​​−x2​​),它的方向也就是最终我们要找的向量的方向。

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！