支持向量机-线性不可分情况

上节回顾

线性可分情况下，支持向量机寻找最佳超平面的优化问题可以表示为：
最 小 化 ( M i n i m i z e ) : 1 2 ∥ ω ∥ 2 限 制 条 件 : y i ( ω T x i + b ) ≥ 1 , ( i = 1 ∼ N ) \begin{aligned} 最小化 (Minimize): & \quad \frac{1}{2} \left\| \omega \right\| ^2 \\ 限制条件: & \quad y_i(\omega^Tx_i + b ) \geq 1 , (i = 1 \sim N) \end{aligned} 最小化(Minimize):限制条件:​21​∥ω∥2yi​(ωTxi​+b)≥1,(i=1∼N)​

线性不可分情况

如果训练样本集是线性不可分的，那么以上优化问题的解，是什么呢？

在稍微思考下，以上的问题，是没有解的。

即：不存在 $\omega 和b$ 满足上面所有的 $N$ 个限制条件。

对于线性不可分的情况，我们要适当的放松限制条件。使上面的最优化问题变得有解。

放松限制条件的基本思路

放 松 限 制 条 件 的 基 本 思 路 ⇓ 对 每 个 训 练 样 本 及 标 签 ( X i , Y i ) ⇓ 松 弛 变 量 δ i ( s l a c k    v a r i a b l e ) \begin{aligned} 放松限制&条件的基本思路 \\ &\Downarrow \\ 对每个训练样&本及标签(X_i,Y_i) \\ &\Downarrow \\ 松弛&变量\delta_i \\ (slack \ \ &variable) \end{aligned} 放松限制对每个训练样松弛(slack  ​条件的基本思路⇓本及标签(Xi​,Yi​)⇓变量δi​variable)​

于是，我们可以将上面的 $N$ 个不等式的限制条件放松为如下的 $N$ 个不等式。
限 制 条 件 改 写 : y i ( ω T X i + b ) ≥ 1 − δ i , ( i = 1 ∼ N ) 限制条件改写: \quad y_i(\omega^TX_i + b) \geq 1 - \delta_i , (i = 1 \sim N ) 限制条件改写:yi​(ωTXi​+b)≥1−δi​,(i=1∼N)
只要松弛变量足够的大，上面的N个不等式的限制条件，是一定能够成立的。

当然，我们还要加入一些新的限制。阻止 δ i \delta_i δi​ 无限制的扩大，让他限制在一定的合理范围之内。。

最终的优化版本
最 小 化 : 1 2 ∣ ∣ ω ∣ ∣ 2 + C ∑ i = 1 N δ i   或   1 2 ∣ ∣ ω ∣ ∣ 2 + C ∑ i = 1 N δ i 2 限 制 条 件 : ( 1 ) δ i ≥ 0 , ( i = 1 ∼ N ) ( 2 ) y i ( w T X i + b ) ≥ 1 − δ i , ( i = 1 ∼ N ) \begin{aligned} 最小化: &\quad \frac{1}{2} \left|| \omega \right|| ^2 + C\sum^N_{i=1} \delta_i \ 或 \ \frac{1}{2} \left|| \omega \right||^2 + C \sum^N_{i=1}\delta_i^2 \\ 限制条件: &\\ &(1)\quad \delta_i \geq 0 , (i = 1\sim N) \\ &(2)\quad y_i(w^TX_i +b) \geq 1- \delta_i,(i=1\sim N) \end{aligned} 最小化:限制条件:​21​∣∣ω∣∣2+Ci=1∑N​δi​ 或 21​∣∣ω∣∣2+Ci=1∑N​δi2​(1)δi​≥0,(i=1∼N)(2)yi​(wTXi​+b)≥1−δi​,(i=1∼N)​
限制条件一，保证了每个δi是大于等于零的；限制条件二，使以前难以达到的不等式变得容易达到。
以 前 的 目 标 函 数 只 需 要 最 小 化    1 2 ∣ ∣ ω ∣ ∣ 2 现 在 的 目 标 函 数 增 加 了 一 项     所 有 δ i 的 和 \begin{aligned} 以前的目标函数只需要最小化 \ \ & \frac{1}{2} \left|| \omega \right||^2 \\ 现在的目标函数增加了一项 \ \ \ & 所有 \delta_i 的和 \end{aligned} 以前的目标函数只需要最小化  现在的目标函数增加了一项   ​21​∣∣ω∣∣2所有δi​的和​
既要让 $\omega$ 越小越好，同时也要让 δ i \delta_i δi​ 越小越好。

其中，有一个比例因子 $C$ ，起到了平衡两项权重的作用。

在实际的应用当中，也可以取另一种目标函数，用 δ i 2 \delta_i^2 δi2​ 代替 δ i \delta_i δi​ ，二者间的差距很小，可以看出，他们都是凸优化问题，都可以被高效的求解

其中比例因子 $C$ 是人为设定的，我们把人为设定的参数叫做算法的超参数（HYPER PARAMETER）。

在实验中，我们会不断变化 $C$ 的值，同时测试算法的识别率，选取效果最好的值作为超参数 $C$ 的取值。

可以看出，如果一个算法的超参数越多，那么手动调参的时间也就越多。这样，算法的自动性也会降低。

支持向量机是超参数很少的算法模型。

超参数很多的模型有人工神经网络，卷积神经网络等等。

以下，是在线性不可分的情况下应用支持向量机的例子。

这里，$C$ 取了 10000，让 $\delta$ 的权重别的很大，使得它本身的值在优化过程中变得很小，接近于零，使得超平面和线性可分情况保持基本一致。
在 线 性 不 可 分 情 况 下 应 用 支 持 向 量 机 取 目 标 函 数 : 1 2 ∣ ∣ ω ∣ ∣ 2 + C ∑ i = 1 N δ i   , C = 10000 超 平 面 和 线 性 可 分 情 况 保 持 基 本 一 致 \begin{aligned} 在线性不可分情&况下应用支持向量机 \\ &取目标函数: \frac{1}{2} \left|| \omega \right|| ^2 + C\sum^N_{i=1} \delta_i \ , C = 10000 \\ &超平面和线性可分情况保持基本一致 \end{aligned} 在线性不可分情​况下应用支持向量机取目标函数:21​∣∣ω∣∣2+Ci=1∑N​δi​ ,C=10000超平面和线性可分情况保持基本一致​

虽然支持向量机求出了一个超平面，但是这个解远远不能让人满意。分错了将近一半的训练样本，跟瞎猜没有区别。

那么问题出在哪里？

我们的算法模型是线性的，也就说我们假设分开两类的函数是直线或超平面，我们是在一簇直线或超平面中选择最适合分开两类样本的一条直线或超平面，但是线性模型的表现力是不够的，在这个例子中，很明显，能分开他们的是某种曲线，例如中间这个椭圆。

如果我们坚持分开两类的必须是直线，无论我们怎么选择，最终的结果都是不能使人满意的，因此，我们只能扩大可选的函数范围。

使他超越线性，才能使他应对各种复杂的线性不可分的情况。

思考

一个模型中的训练样本如下图所示，问能否对 X 1 , X 2 X_1,X_2 X1​,X2​ 两个向量做某种非线性变换，把本来线性不可分的训练样本集变为线性可分？

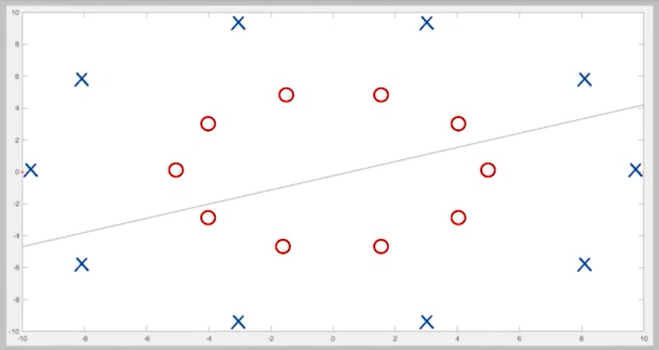
低维到高维映射

如何扩大可选函数的范围，从而提高支持向量机处理非线性可分问题的能力？

支持向量机在这方面是独树一帜的，其他的算法比如人工神经网络、决策树等是直接产生更多可选函数。

例如在人工神经网络中，通过多层非线性函数的组合，能够产生类似于椭圆这样的曲线，从而分开这幅图中圆圈和叉。

支持向量机却不是直接产生，而是通过将特征空间由低维映射到高维，然后在高维的特征空间中，仍然用线性的超平面对数据进行分类。下面给出两张直观的图片。

再给一个具体的例子，这是一个在低维线性不可分，而在高维中线性可分的例子。考察如下图所示的训练样本。

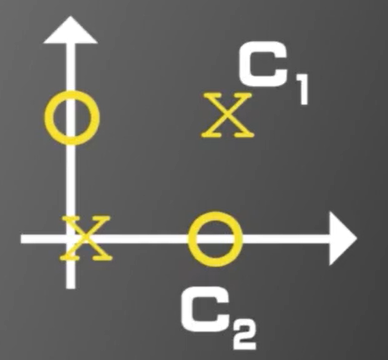
x 1 = [ 0 0 ] ∈ C 1 x 2 = [ 1 1 ] ∈ C 1 x 3 = [ 1 0 ] ∈ C 2 x 4 = [ 0 1 ] ∈ C 2 x_1 = \begin{bmatrix} 0 \\ 0 \end{bmatrix} \in C_1 \qquad x_2 = \begin{bmatrix} 1 \\ 1 \end{bmatrix} \in C_1 \qquad x_3 = \begin{bmatrix} 1 \\ 0 \end{bmatrix} \in C_2 \qquad x_4 = \begin{bmatrix} 0 \\ 1 \end{bmatrix} \in C_2 \qquad x1​=[00​]∈C1​x2​=[11​]∈C1​x3​=[10​]∈C2​x4​=[01​]∈C2​

构造一个二维到五维的映射 $\phi (x)$
φ ( x ) : x = [ a b ] → φ ( x ) = [ a 2 b 2 a b a b ] \varphi(x) : x = \begin{bmatrix} a \\ b \end{bmatrix} \rightarrow \varphi(x) = \begin{bmatrix} a^2 \\ b^2 \\a \\ b \\ ab \end{bmatrix} φ(x):x=[ab​]→φ(x)=⎣⎢⎢⎢⎢⎡​a2b2abab​⎦⎥⎥⎥⎥⎤​
那么，可以得到如下经过变换的四个样本：
φ ( x 1 ) = [ 0 0 0 0 0 ] φ ( x 2 ) = [ 1 1 1 1 1 ] φ ( x 3 ) = [ 1 0 1 0 0 ] φ ( x 4 ) = [ 0 1 0 1 0 ] \varphi(x_1) = \begin{bmatrix} 0 \\ 0 \\0 \\ 0 \\ 0 \end{bmatrix} \qquad \varphi(x_2) = \begin{bmatrix} 1 \\ 1\\1 \\ 1 \\ 1 \end{bmatrix} \qquad \varphi(x_3) = \begin{bmatrix} 1 \\ 0 \\1 \\ 0 \\ 0 \end{bmatrix} \qquad \varphi(x_4) = \begin{bmatrix} 0 \\ 1 \\0 \\ 1 \\ 0 \end{bmatrix} \qquad φ(x1​)=⎣⎢⎢⎢⎢⎡​00000​⎦⎥⎥⎥⎥⎤​φ(x2​)=⎣⎢⎢⎢⎢⎡​11111​⎦⎥⎥⎥⎥⎤​φ(x3​)=⎣⎢⎢⎢⎢⎡​10100​⎦⎥⎥⎥⎥⎤​φ(x4​)=⎣⎢⎢⎢⎢⎡​01010​⎦⎥⎥⎥⎥⎤​
经过此变换，原问题变得线性可分。
设 ： ω = [ − 1 − 1 − 1 − 1 6 ] b = 1 ω T φ ( x 1 ) + b = 1 ≥ 0 ω T φ ( x 2 ) + b = 3 ≥ 0 ω T φ ( x 3 ) + b = − 1 < 0 ω T φ ( x 4 ) + b = − 1 < 0 经 由 二 维 到 五 维 的 映 射 φ ( x ) 线 性 不 可 分 ⇓ 线 性 可 分 \begin{aligned} 设： \omega = \begin{bmatrix} -1 \\ -1 \\ -1 \\-1 \\ 6 \end{bmatrix} & \qquad b=1 \\ \omega^T\varphi(x_1)+b=1 \geq 0 & \qquad \omega^T\varphi(x_2)+b=3 \geq 0 \\ \omega^T\varphi(x_3)+b=-1 \lt 0 & \qquad \omega^T\varphi(x_4)+b=-1 \lt 0 \\ \\ 经由二维到&五维的映射\varphi(x) \\ 线性&不可分 \\ &\Downarrow \\ 线&性可分 \end{aligned} 设：ω=⎣⎢⎢⎢⎢⎡​−1−1−1−16​⎦⎥⎥⎥⎥⎤​ωTφ(x1​)+b=1≥0ωTφ(x3​)+b=−1<0经由二维到线性线​b=1ωTφ(x2​)+b=3≥0ωTφ(x4​)+b=−1<0五维的映射φ(x)不可分⇓性可分​
我们这里不加证明的给出一个定理。
定理： 在 一 个 M 维 空 间 上 随 机 取 N 个 训 练 样 本 ， 随 机 的 对 每 个 训 练 样 本 赋 予 标 签 + 1 或 − 1 假 设 : 这 些 训 练 样 本 线 性 可 分 的 概 率 为 P ( M ) 当 M → ∞ 时 ， P ( M ) = 1 \begin{aligned} &\textbf{定理：} \newline \\ &&&在一个M维空间上随机取N个训练样本，随机的对每个训练样本赋予标签 +1 或 -1 \newline \\ &假设: \newline \\ &&&这些训练样本线性可分的概率为P(M) \newline \\ &&&当 \quad M \rightarrow \infty \quad 时，\quad P(M)=1 \end{aligned} ​定理：假设:​​在一个M维空间上随机取N个训练样本，随机的对每个训练样本赋予标签+1或−1这些训练样本线性可分的概率为P(M)当M→∞时，P(M)=1​
当特征空间的维度 $M$ 增加时，待估计参数 $(\omega ,b)$ 的维度也在跟随增加。

同时，整个算法模型的自由度也随之增加。

当然，这就更有可能分开低维空间无法分开的数据。
将 训 练 样 本 由 低 维 映 射 到 高 维 ⇓ 增 大 线 性 可 分 的 概 率 \begin{aligned} 将训练样本&由低维映射到高维 \newline \\ &\Downarrow \newline \\ 增大线性&可分的概率 \end{aligned} 将训练样本增大线性​由低维映射到高维⇓可分的概率​
那么如何设计这个 $\phi (x)$ 就成为最关键的问题。

我们先放下对 $\phi (x)$ 的具体形式的探讨，先假设 $\phi (x)$ 已经确定。

来观察支持向量机优化问题将会做什么样的改变。
低 维 : 最 小 化 : 1 2 ∣ ∣ ω ∣ ∣ 2 + C ∑ i = 1 N δ i   或   1 2 ∣ ∣ ω ∣ ∣ 2 + C ∑ i = 1 N δ i 2 限 制 条 件 : ( 1 )   δ i ≥ 0 , ( i = 1 ∼ N ) ( 2 )   y i ( w T X i + b ) ≥ 1 − δ i , ( i = 1 ∼ N ) ⇓ x → φ ( x ) 高 维 : 最 小 化 : 1 2 ∣ ∣ ω ∣ ∣ 2 + C ∑ i = 1

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！