非线性数据结构之二叉树
目录
一.了解树形结构
1.树形结构图
2.树的有关概念
3.树的表示结构
二.认识二叉树
1.什么是二叉树
2.特殊的二叉树
(1)满二叉树
(2)完全二叉树
3.二叉树的一些性质
4.二叉树的基本操作
(1)二叉树的存储
(2)二叉树的基本操作
(3)代码实现二叉树的创建和前中后递归遍历
一.了解树形结构
树是一种非线性的数据结构,它是由n(n>=0)个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。
1.树形结构图
注意:树结构不能有交集,否则就变为了图结构。
如图所示:
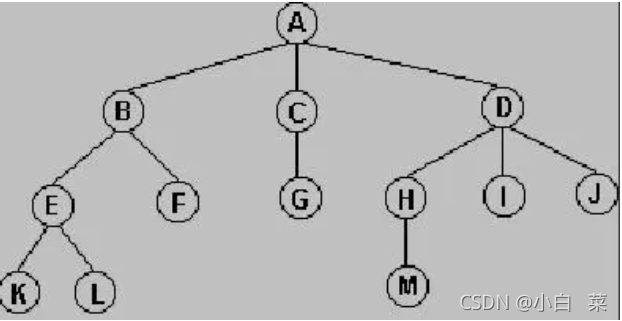
2.树的有关概念
(1)其中A没有前驱只有后继,称为根结点。K,L,F,M,I,J称为叶子结点,叶子结点只有前驱,没有后继。
(2)结点的度:该结点子树的个数,上图A的度为3;树的度:该树中所有结点度的最大值,上图树的度为3。
(3)树的深度:从根结点开始为第1层,依次往下,上图树深度为4。
(4)兄弟结点:同一个双亲结点的结点。堂兄弟结点:双亲在同一层。
(5)有m棵互不相交的树为森林(m>=0).
3.树的表示结构
(1)双亲表示法
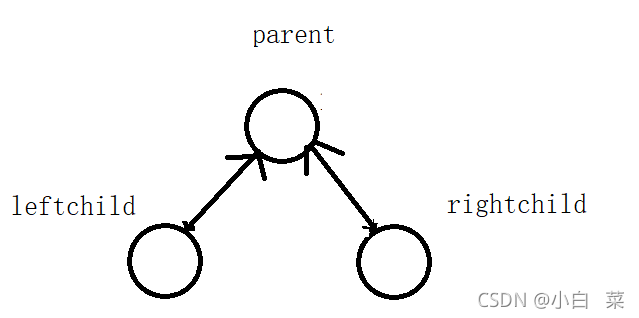
(2)孩子表示法:通过给结点设置左引用和右引用来表示左右孩子
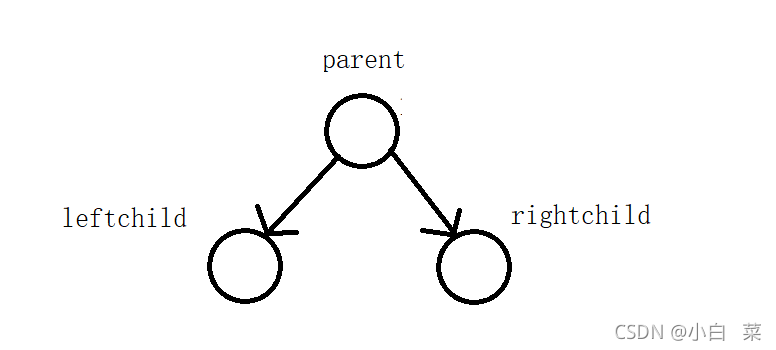
(3)孩子双亲表示法
(4)孩子兄弟表示法

4.树的应用
电脑或手机中的文件管理就是按照树的结构来进行管理。
二.认识二叉树
1.什么是二叉树
二叉树中每一个子树的度都不大于2,每一个子树只有左子树和右子树之分,要么存在,要么为空。
以下都为二叉树
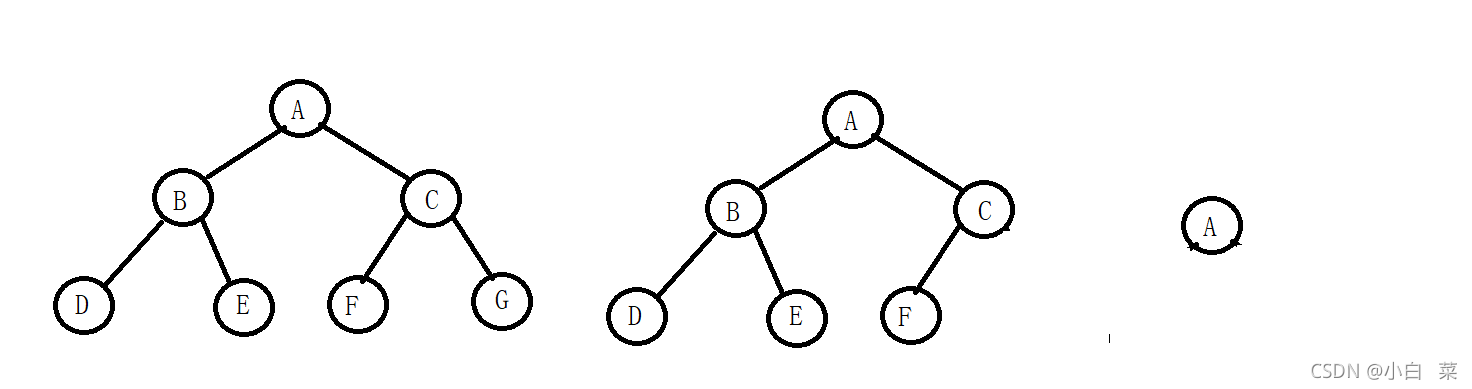
2.特殊的二叉树
(1)满二叉树
一棵二叉树,如果每层的结点数都达到最大值,则这棵二叉树就是满二叉树。也就是说,如果一棵
二叉树的层数为K,且结点总数是 ,则它就是满二叉树。
每一层结点数都为该层结点数的最大值。

(2)完全二叉树
结构为满二叉树的一个子结构。

注意:下面的二叉树不是完全二叉树

3.二叉树的一些性质
(1) 若规定根结点的层数为1,则一棵非空二叉树的第i层上最多有 二叉树的存储分为顺序存储和链式存储。 其中的链式存储是根据一个一个的结点引用来进行连接,下面关于二叉树的一些基本操作是根据孩子表示法来进行存储的。 1.二叉树的创建 这里对于二叉树的创建是根据所给的前序遍历结果的数组中的值来进行创建的 2.递归遍历二叉树 前序遍历:访问根结点--->根的左子树--->根的右子树 先将跟的结果进行打印,然后递归接着往左子树中找根结点,左子树遍历完后再往右子树中重新开始根左右的操作即可。 前序遍历递归示意图: 中序遍历:根的左子树--->根节点--->根的右子树 后序遍历:根的左子树--->根的右子树--->根节点 中序和后序示意图和上面类似,只不过执行的顺序不同。![]() (i>0)个结点
(i>0)个结点
(2)若规定只有根结点的二叉树的深度为1,则深度为K的二叉树的最大结点数是 2^k - 1(k>=0)
(3) 对任何一棵二叉树, 如果其叶结点个数为 n0, 度为2的非叶结点个数为 n2,则有n0=n2+1
(4)具有n个结点的完全二叉树的深度k为 ![]() 上取整
上取整
(5) 对于具有n个结点的完全二叉树,如果按照从上至下从左至右的顺序对所有节点从0开始编号,则对于序号为i的结点有:
若i>0,双亲序号:(i-1)/2;i=0,i为根结点编号,无双亲结点
若2i+1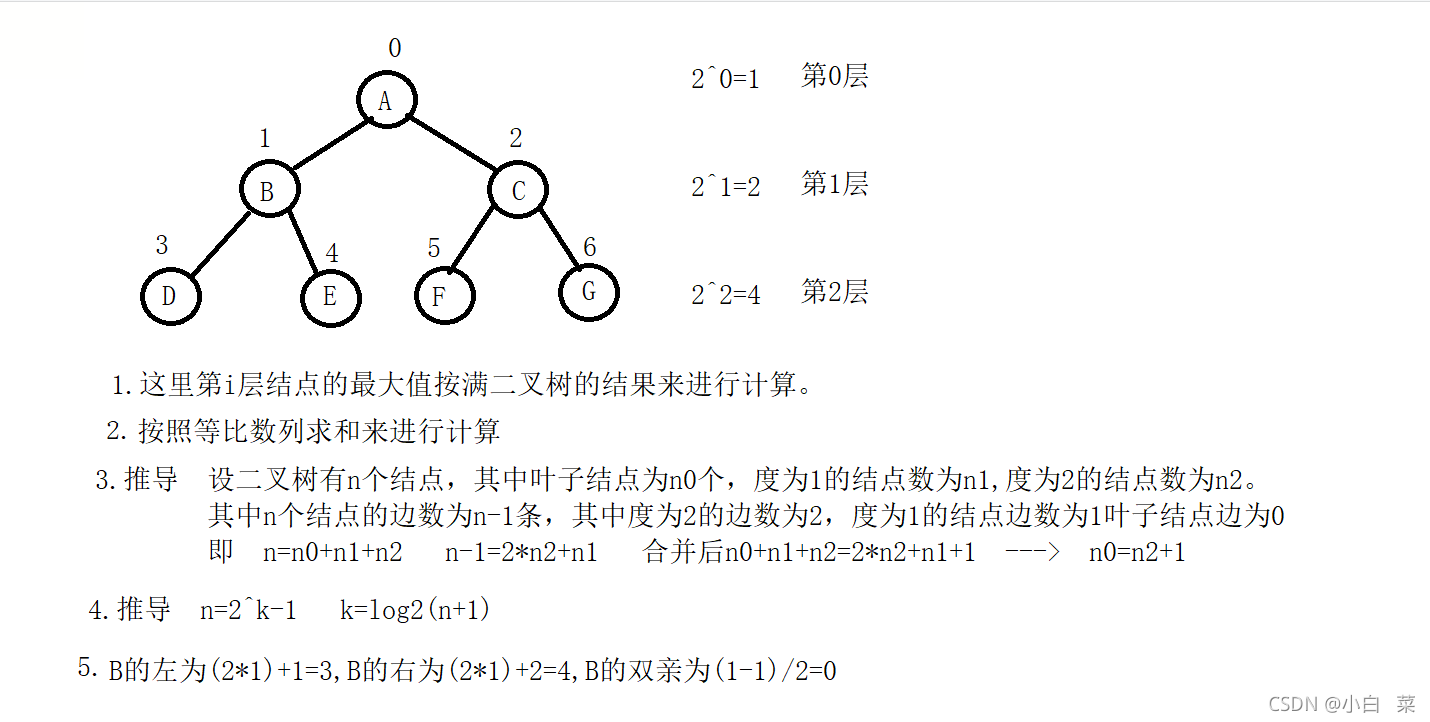
4.二叉树的基本操作
(1)二叉树的存储
(2)二叉树的基本操作


(3)代码实现二叉树的创建和前中后递归遍历
package structdata.binarytree;public class MyBinaryTree {public static void main(String[] args) {BinaryTree bt = new BinaryTree();int[] arr= {1,2,3,-1,-1,-1,4,5,-1,-1,6};bt.createTree(arr);bt.preOrder();//123456bt.inOrder();//321546bt.postOrder();//325641}}
class BinaryTree {private Node root;private int index;public Node createTree(int[] arr){return createTree(root,arr);}//递归创建二叉树private Node createTree(Node troot,int[] arr) {if(index>=arr.length){return null;}if(arr[index]!=-1){Node node=new Node(arr[index]);troot=node;++index;troot.left= createTree(troot.left,arr);++index;troot.right = createTree(troot.right,arr);}return root=troot;}public void preOrder() {System.out.println("前序遍历");preoOrder(root);System.out.println();}public void inOrder(){System.out.println("中序遍历");inOrder(root);System.out.println();}public void postOrder(){System.out.println("后序遍历");postOrder(root);System.out.println();}//前序(根左右)private void preoOrder(Node treeRoot) {if (treeRoot != null) {System.out.print(treeRoot.val + " ");preoOrder(treeRoot.left);preoOrder(treeRoot.right);}}//中序(左根右)private void inOrder(Node treeRoot){if(treeRoot!=null){inOrder(treeRoot.left);System.out.print(treeRoot.val+" ");inOrder(treeRoot.right);}}//后序(左右根)private void postOrder(Node treeNode){if(treeNode!=null){postOrder(treeNode.left);postOrder(treeNode.right);System.out.print(treeNode.val+" ");}}}
//定义结点
class Node{int val;Node left;Node right;public Node(int val) {this.val = val;}
}
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!