矩阵相乘最少计算次数问题

矩阵相乘最少计算次数

题目描述

不同的计算顺序的乘法计算次数是不一样的，如 $(AB)C$ 和 $A(BC)$的乘法计算次数分别为 p 0 p 1 p 2 + p 0 p 2 p 3 p_0p_1p _2 + p_0p_2p_3 p0​p1​p2​+p0​p2​p3​ 和 p 1 p 2 p 3 + p 0 p 1 p 3 p_1p_2 p_3 + p_0p_1p_3 p1​p2​p3​+p0​p1​p3​。

$n$ 个矩阵相乘 A 1 A 2 ⋅ ⋅ ⋅ A n A_1A_2···A_n A1​A2​⋅⋅⋅An​，矩阵 A i A_i Ai​的维度为 p i − 1 × p i p_{i-1}×p_i pi−1​×pi​，求$n$ 个矩阵相乘的最少计算次数。

题目分析

矩阵 A m n B n k A_{mn}B_{nk} Amn​Bnk​的乘法计算次数为 $m\times n\times k$。

N个矩阵相乘， A 1 A 2 ⋅ ⋅ ⋅ A n A_1A_2···A_n A1​A2​⋅⋅⋅An​可以看作一个多部决策的问题 A 1 A 2 ⋅ ⋅ ⋅ A n A_1A_2···A_n A1​A2​⋅⋅⋅An​可以分成 ( A 1 A 2 ⋅ ⋅ ⋅ A k ) ( A k + 1 A 2 ⋅ ⋅ ⋅ A n ) (A_1A_2···A_k)(A_{k+1}A_2···A_n) (A1​A2​⋅⋅⋅Ak​)(Ak+1​A2​⋅⋅⋅An​)两部分相乘，再依次对每个子部分进行划分。

令$OPT(i,j)$表示 A i A i + 1 ⋅ ⋅ ⋅ A j A_iA_{i+1}···A_j Ai​Ai+1​⋅⋅⋅Aj​所需要的最少乘法次数，那么：
O P T ( i , j ) = { 0 if  i = j min ⁡ i ≤ k ≤ j ( O P T ( i , k ) + O P T ( k + 1 , j ) + p i − 1 p k p j ) otherwise OPT(i, j) = \begin{cases} 0 &\text{if } i =j \\ \min_{i\leq k \leq j} (OPT(i, k) + OPT(k+1, j) + p_{i-1}p_kp_j )&\text{otherwise} \end{cases} OPT(i,j)={0mini≤k≤j​(OPT(i,k)+OPT(k+1,j)+pi−1​pk​pj​)​if i=jotherwise​

算法一

上述算法的伪代码如下：

上述算法的复杂度：
T ( n ) = ∑ k = 1 n − 1 ( T ( k ) + T ( n − k ) + O ( 1 ) ) T(n) = \sum_{k=1}^{n-1} (T(k) + T(n-k) + O(1)) T(n)=k=1∑n−1​(T(k)+T(n−k)+O(1))
数学归纳法证明上述算法的复杂度为指数级别 T ( n ) = O ( 2 n − 1 ) T(n)=O(2^{n-1}) T(n)=O(2n−1)，推导部分的过程， $n>2$ 时：
T ( n ) = ∑ k = 1 n − 1 ( T ( k ) + T ( n − k ) + O ( 1 ) ) = 2 ∑ k = 1 n − 1 T ( k ) + O ( n − 1 ) ≥ 2 ∑ k = 1 n − 1 2 k − 1 + n − 1 ≥ 2 n − 2 + n − 1 ≥ 2 n − 1 = O ( 2 n − 1 ) \begin{aligned} T(n) &= \sum_{k=1}^{n-1} (T(k) + T(n-k) + O(1)) \\ &= 2\sum_{k=1}^{n-1} T(k)+O(n-1) \\ &\geq 2\sum_{k=1}^{n-1} 2^{k-1}+n -1\\ &\geq 2^n -2 + n -1\\ & \geq 2^{n-1} = O(2^{n-1}) \end{aligned} T(n)​=k=1∑n−1​(T(k)+T(n−k)+O(1))=2k=1∑n−1​T(k)+O(n−1)≥2k=1∑n−1​2k−1+n−1≥2n−2+n−1≥2n−1=O(2n−1)​

优化一

上述算法时间复杂度非常高的原因是因为存在很多冗余计算，类似于斐波那契数列 $f(n)=f(n-1)+f(n-2)$，在递归过程中很多 $OPT(i,j)$会被重复计算。设置一个记忆数组 $OPT[i,j]$保存已经计算过的 $OPT(i,j)$来避免重复计算。

时间复杂度简化为 O ( n 3 ) O(n^3) O(n3)，可以看成求解一个 $OPT[i,j]$的数组，大小为 $n\times n$，即需要计算 O ( n 2 ) O(n^2) O(n2)次，每个元素的求解的复杂度为 $O(n)$ （遍历区间 $[i,j]$ 内所有的 $k$ ），所以算法复杂度为 O ( n 3 ) O(n^3) O(n3)。

优化二

使用数组去掉递归过程（空间优化，时间复杂度不变）。

回溯寻找计算顺序

必须再求出最优解之后，才能回溯寻找最优计算序列。
根据每次计算时的 $k$，回溯寻找最优序列。

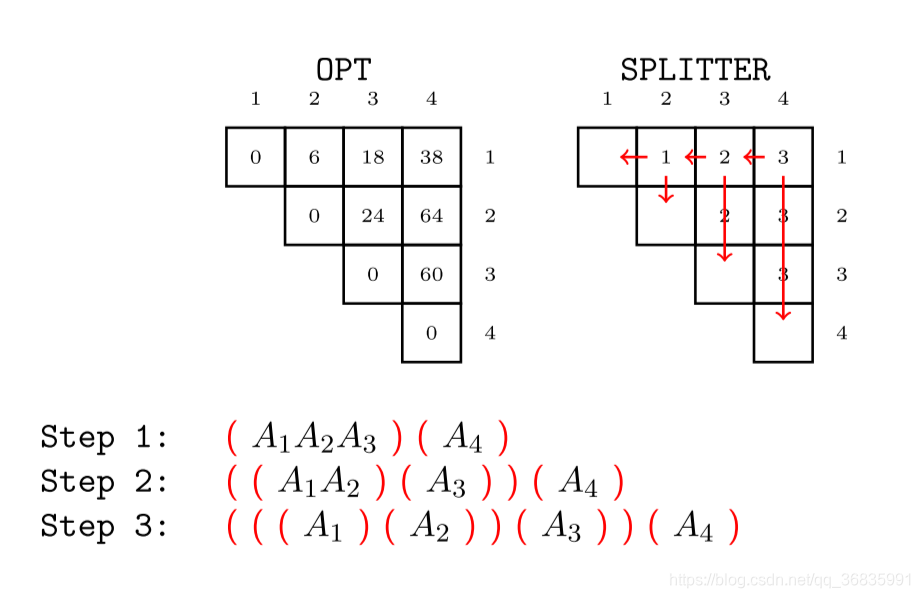
算法四

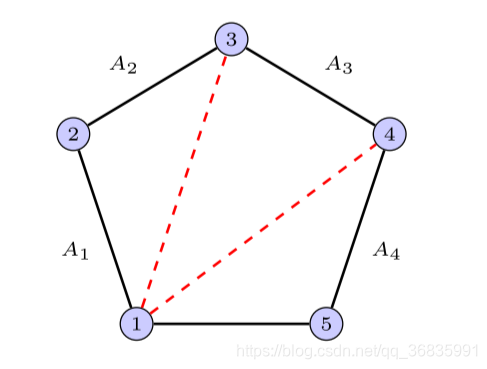
$n$ 个矩阵依次构成一个 $n+1$边形的前 $n$ 条边，每条边根据矩阵的维度存在一个权重，那么对多边形进行三角化分（划分成多个三角形），红边代表划分的三角的边，其权重由多边形的边的权重相乘得到。最少乘法计算量即所有红边的权重和最小。

See Hu and Shing 1981论文提出了 $O(n\log n)$的算法，过于复杂本文不再介绍。

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！