【机器学习】白话朴素贝叶斯算法
朴素贝叶斯
- 一、条件概率
- 二、贝叶斯公式
- 三、贝叶斯公式的应用
- 四、朴素贝叶斯代码
朴素贝叶斯算法依据概率论中 贝叶斯定理建立的模型,前提假设是 各个特征之间相互独立(这也是**“朴素”的含义**),因为实际场景中多个特征一般存在相关性,所以针对特征之间存在强相关性的场景往往会分类不准。朴素贝叶斯算法最常见的应用场景是垃圾邮件分类。
一、条件概率
定义:条件概率是指事件A在事件B发生的条件下发生的概率,条件概率表示为:P(A|B)。
为了更加清楚的理解这个公式的背景,我们现在假设一个古典的概率场景:有一个装了7个石块的罐子,其中4块是红色的,3块是白色的。
- Q1:如果从罐子里面随机取出一块石头,那么是白色的可能性有多大?
- A1:根据古典概型的计算公式:P(white)=3/7 ,同样地,可以知道取出红色石头的概率是4/7.
现在呢,我们将这7块石头分别放到两个桶中,并且标记为A桶和B桶,其中A桶:2块白色、2块红色;B桶:1块白色、2块红色,现在再让你计算取出的石头是红色还是白色的概率。由于石头分配的信息量不同,我们把从A桶中取出白色石头的概率记作P(white | A),理解为:已知从A桶取出石头的条件下,取出白色石头的概率,也就是条件概率啦。P(white|A)=1/2
假如我们仍然将A、B两桶中的7块石头看作是一个系统,那么取出的石头来自A桶的概率为4/7 ,很好理解,因为系统中的7块石头有4块是属于A桶的;但是这块从A桶中取出的石头又恰好是白色的概率呢?P(A and white) = 4/7*2/4=2/7
所以就推导出了条件概率的公式:
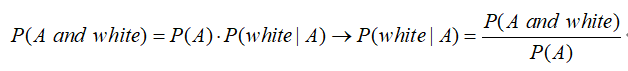
根据上面的场景验证一下这个公式:
- P(A and white):从A桶中取出并且是白色 = 2/7
- P(A):从A桶中取出石头的概率 = 4/7
- P(white | B):已知是从A桶中取得的,且石头为白色 = 1/2
二、贝叶斯公式
已知事件A在事件B发生的条件下发生的概率是
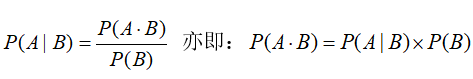
理解为:条件A和B同时发生的概率等于B事件发生的概率乘以B条件下A事件发生的概率。
 这个就是大名鼎鼎的贝叶斯公式了。贝叶斯公式告诉我们如何交换条件概率的条件与结果,即如果已知
这个就是大名鼎鼎的贝叶斯公式了。贝叶斯公式告诉我们如何交换条件概率的条件与结果,即如果已知P(B | A),要求P(A | B),可以使用上述计算方法。
三、贝叶斯公式的应用
逆概问题:人们已经能够根据古典概型计算“正向概率”(先验概率),如“假设袋子里面有N个白球,M个黑球,你伸手进去摸,摸出黑球的概率是多大”。 反过来,一个自然而然的问题是:“如果我们事先并不知道袋子里面黑白球的比例,而是闭着眼睛摸出一个(或好几个)球,观察这些取出来的球的颜色之后,那么我们可以就此对袋子里面的黑白球的比例作出什么样的推测”。就是所谓的逆向概率问题。
这背后的深刻原因在于,现实世界本身就是不确定的,人类的观察能力是有局限性的。沿用刚才那个袋子里面取球的比方,我们往往只能知道从里面取出来的球是什么颜色,而并不能直接看到袋子里面实际的情况。
例:讨论学生是否会购买电脑的分类问题,我们收集了如下的数据集:
| Age | Income | Student | Credit_rating | Buys_computer |
|---|---|---|---|---|
| <=30 | high | no | fair | no |
| <=30 | high | no | excellent | no |
| 31~40 | high | no | fair | yes |
| >40 | medium | no | fair | yes |
| >40 | low | yes | fair | yes |
| >40 | low | yes | excellent | no |
| 31~40 | low | yes | excellent | yes |
| <=30 | medium | no | fair | no |
| <=30 | low | yes | fair | yes |
| >40 | medium | yes | fair | yes |
| <=30 | medium | no | excellent | yes |
| 31~40 | medium | no | excellent | yes |
| 31~40 | high | yes | fair | yes |
| >40 | medium | no | excellent | no |
现在又来了一个新样本是:X = (age≤30,Income=Medium,Student=yes,Credit_rating=Fair),请你预测这个未知元组X是否会购买电脑。

这是属于一个二分类的问题,同理,可以计算出这个元组X的Buys_computer中no的概率如下:

贝叶斯分类器的基本方法:在统计资料的基础上,依据某些特征,计算各个类别的概率,从而实现分类。朴素贝叶斯方法的优势在于它易于实现,而且在大多数情况下能够获得较好的分类准确率。它的劣势在于它的类条件独立性假设,如果数据的各个属性之间有比较强的依赖关系,朴素贝叶斯方法往往不能取得较好的结果。
上面分类的过程有一个小细节,不知道读者有没有注意到,那就是忽略了
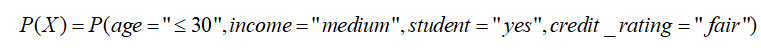
的计算,实际根据已有的样本进行计算时,等于0,导致了分母为0的情况发生。
拉普拉斯修正:由于特征空间较为稀疏,因此,常常出现概率为0的情况,在这种情况下,需要对其进行一些修正。常见的修正方法是拉普拉斯修正法,就是使得计算条件概率时,分子加1。
四、朴素贝叶斯代码
- 运行环境:Jupyter Notebook
- 数据集:学生基本信息表
# 读取学生基本信息
import numpy as np
import pandas as pd
df = pd.read_table(r'.\学生基本信息表.txt',encoding='utf8',delimiter=',
',index_col=0)
# 由于所提供的数据中包含了字母字符串,需要对数据进一步处理
'''Age 1-3代表 <=30 31~40 >40 Income 1-3代表 low medium high Student 0-1代表 no yes Credit_rating 1-2代表 fair excellent Buys_computer 0-1代表 no yes
'''
df['Age']=df['Age'].map({'<=30':1,'31~40':2,'>40':3})
df['Income']=df['Income'].map({'low':1,'medium':2,'high':3})
df['Student']=df['Student'].map({'no':0,'yes':1})
df['Credit_rating']=df['Credit_rating'].map({'fair':1,'excellent':2})
df['Buys_computer']=df['Buys_computer'].map({'no':0,'yes':1})
Xtrain = df.iloc[:,:-1]
Xtrain = np.array(Xtrain)
# 标签
Ytrain = df.iloc[:,-1]
from sklearn.naive_bayes import GaussianNB #高斯朴素贝叶斯
'''
GaussianNB 参数只有一个:先验概率priors
MultinomialNB参数有三个:alpha是常量,一般取值1,fit_prior是否考虑先验概率,class_prior自行输入先验概率
BernoulliNB参数有四个:前三个与MultinomialNB一样,第四个binarize 标签二值化
'''
# 构建模型
clf = GaussianNB()
# 拟合:训练模型
clf.fit(Xtrain,Ytrain)
# 数据样本是X=(age<=30, Income=Medium, Student=yes, Credit_rating=Fair)
X_pre = np.array([[1,2,1,1]]) # 预测
result = clf.predict(X_pre)
if result == 1:print("分类结果:Buys_computer='yes'")
else:print("分类结果:Buys_computer='no'")
由于算法的数学计算比较多,涉及太多公式,造成阅读不便还请谅解!
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!