机器人中的数值优化|【五】BFGS算法非凸/非光滑处理

机器人中的数值优化|【五】BFGS算法的非凸/非光滑处理

往期内容回顾

机器人中的数值优化|【一】数值优化基础
机器人中的数值优化|【二】最速下降法，可行牛顿法的python实现，以Rosenbrock function为例
机器人中的数值优化|【三】无约束优化，拟牛顿法理论与推导
机器人中的数值优化|【四】L-BFGS理论推导与延伸

在往期中我们对拟牛顿法以及BFGS等算法进行了详细的推导和学习，但是之前讨论的都为在保证函数凸且光滑的情况，那么如果函数非凸或者非光滑呢？我们在本节中进行一下研究。

非光滑的函数BFGS优化算法

Weak Wolfe Condition

sufficient decrease condition:
S ( α ) : f ( x k ) − f ( x k + α d ) ≥ − c 1 α d T ∇ f ( x k ) S(\alpha):f(x^k)-f(x^k+\alpha d)\ge-c_1 \alpha d^T\nabla f(x^k) S(α):f(xk)−f(xk+αd)≥−c1​αdT∇f(xk)

curvature condition:
C ( α ) : d T ∇ f ( x k + α d ) ≥ c 2 d T ∇ f ( x k ) C(\alpha):d^T\nabla f(x^k+\alpha d)\ge c_2 d^T \nabla f(x^k) C(α):dT∇f(xk+αd)≥c2​dT∇f(xk)

Lewis & Overton line search:

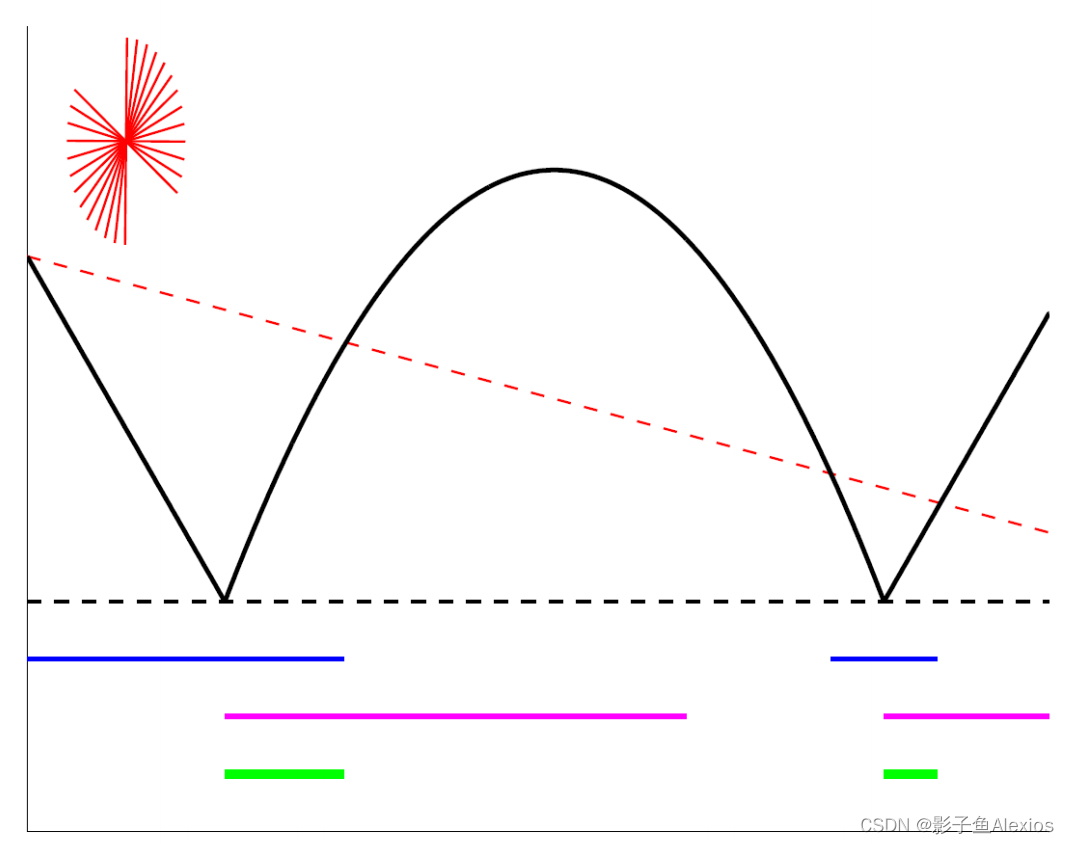
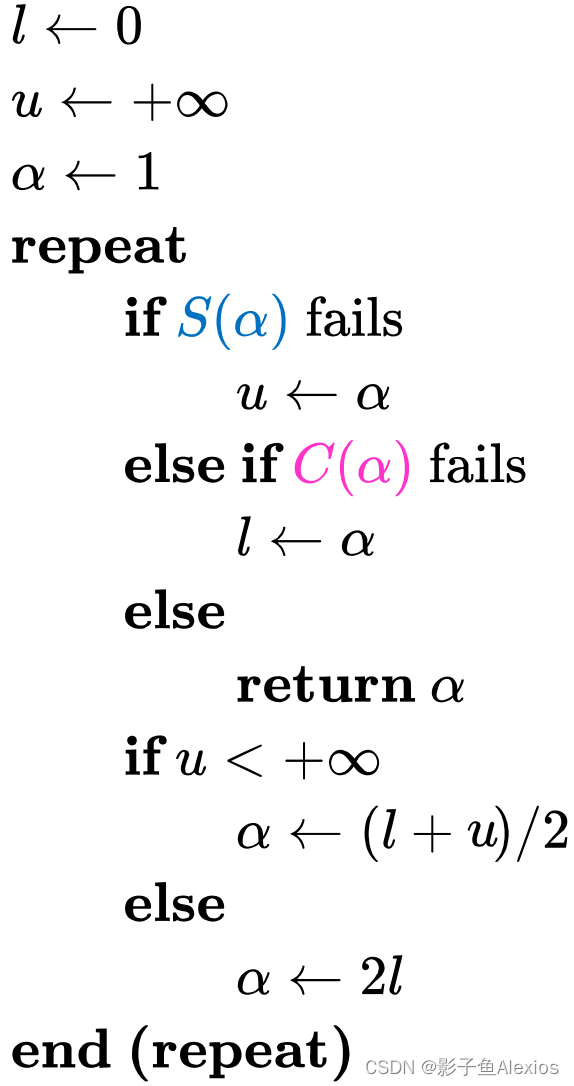
非凸但平滑的函数BFGS优化算法

Cautious-Limited-Memory-BFGS

非凸非平滑函数的BFGS优化算法

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！