【C++天梯计划】1.5 排列组合(Permutation and Combination)

文章目录

• • 定义及公式
  • 例题1：全排列
  • • • 题目描述
      • 输入格式
      • 输出格式
      • 输入输出样例
      • 说明/提示
      • 代码：
  • 例题2：素数环
  • • • 题目描述
      • 输入格式
      • 输出格式
      • 输入输出样例
      • 代码：

🎆🎉🎉🎉🎉🎉🎉🎉🎉🎉🎉🎆
今天我要开启一个新计划----【C++天梯计划】
目的是通过天梯计划，通过题目和知识点串联的方式，完成C++复习与巩固。

定义及公式

排列的定义：从n个不同元素中，任取m(m≤n,m与n均为自然数,下同）个不同的元素按照一定的顺序排成一列，叫做从n个不同元素中取出m个元素的一个排列；从n个不同元素中取出m(m≤n）个元素的所有排列的个数，叫做n个不同元素中取出m个元素的排列数，用符号A(n,m)或Amn表示
计算公式：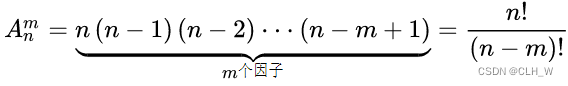

例题1：全排列

题目描述

定义两个长为 nn 的排列 AA 与 BB 相似：若 \forall i∀i，满足 C(A, A_i) = C(B, B_i)C(A,A i​ )=C(B,B i​ )。其中 C(P, x)C(P,x) 为满足 P_j < xP j​ 对于两个长为 nn 的排列 P_1, P_2P
1​ ,P 2​ ，定义函数 F(P_1, P_2)F(P 1 ,P 2​ ) 等于满足 P_1[l \ldots r]P 1
[l…r] 相似于 P_2[l \ldots r]P 2 [l…r] (1 \leqslant l \leqslant r \leqslant n)(1⩽l⩽r⩽n) 并且 P_1[l \ldots r]P 1
​ [l…r] 包含不超过 EE 个逆序对的数对 (l, r)(l,r) 的数目。
现在请你求出：对 P_1, P_2P 1 ,P 2 分别取遍所有 1 \sim n1∼n 的排列后所有 F(P_1, P_2)F(P 1 ,P 2 ) 的和。

输入格式

第一行一个整数 TT 表示数据组数。
接下来 TT 行，每行包含两个非负整数 n, En,E。

输出格式

对于每组数据，输出一行一个整数表示答案模 10^9 + 710 9 +7。

输入输出样例

输入 #1
4
2 2
2 1
2 0
1 1
输出 #1
10
10
9
1

说明/提示

对于 50%50% 的数据，T \leqslant 10^4, n \leqslant 10, E \leqslant 50T⩽10 4
,n⩽10,E⩽50。对于 80%80% 的数据，T \leqslant 10^4, n \leqslant 50, E \leqslant 10^6T⩽10 4 ,n⩽50,E⩽10 6 。对于 100%100% 的数据，T \leqslant 10^4, n \leqslant 500, E \leqslant 10^6T⩽10 4 ,n⩽500,E⩽10 6 。

代码：

#include 
#include 
#include 
int read() {int res = 0, c;doc = getchar();while (c < '0' || c > '9');while ('0' <= c && c <= '9') {res = res * 10 + c - '0';c = getchar();}return res;
}
const int size = 505, mod = 1000000007;
int add(int a, int b) {a += b;return a < mod ? a : a - mod;
}
int sub(int a, int b) {a -= b;return a >= 0 ? a : a + mod;
}
std::vector<int> cnt[size];
int C[size][size], fac[size];
typedef long long Int64;
#define asInt64(x) static_cast<Int64>(x)
void pre(int n, int m) {fac[0] = 1;for (int i = 1; i <= n; ++i) fac[i] = asInt64(fac[i - 1]) * i % mod;C[0][0] = 1;for (int i = 1; i <= n; ++i) {C[i][0] = 1;for (int j = 1; j <= i; ++j)C[i][j] = add(C[i - 1][j - 1], C[i - 1][j]);}cnt[0].push_back(1);for (int i = 1; i <= n; ++i) {int lsiz = cnt[i - 1].size();int cur = std::min(m, i * (i - 1) / 2);cnt[i].resize(cur + 1);cnt[i][0] = 1;for (int j = 1; j <= cur; ++j) {cnt[i][j] = cnt[i][j - 1];if (j < lsiz) cnt[i][j] = add(cnt[i][j], cnt[i - 1][j]);int off = j - i;if (0 <= off && off < lsiz)cnt[i][j] = sub(cnt[i][j], cnt[i - 1][off]);}}for (int i = 1; i <= n; ++i) {int siz = cnt[i].size();for (int j = 1; j < siz; ++j)cnt[i][j] = add(cnt[i][j - 1], cnt[i][j]);}
}
int query(int n, int m) {int res = 0;for (int i = 1; i <= n; ++i) {Int64 val = asInt64(C[n][i]) * fac[n - i] % mod;int cur = cnt[i].size() - 1;res = (res + val * val % mod * cnt[i][std::min(cur, m)] % mod * (n - i + 1)) % mod;}return res;
}
struct Query {int n, m;
} Q[10005];
int main() {int t = read();int maxn = 0, maxm = 0;for (int i = 0; i < t; ++i) {Q[i].n = read();maxn = std::max(maxn, Q[i].n);Q[i].m = read();maxm = std::max(maxm, Q[i].m);}pre(maxn, maxm);for (int i = 0; i < t; ++i)printf("%d\n", query(Q[i].n, Q[i].m));return 0;
}

例题2：素数环

题目描述

从 11~nn 这 nn 个数，摆成一个环，要求相邻的两个数的和是素数，按照由小到大请输出所有可能的摆放形式。
比如：n = 4n=4，输出形式如下；
1:1 2 3 4
2:1 4 3 2
3:2 1 4 3
4:2 3 4 1
5:3 2 1 4
6:3 4 1 2
7:4 1 2 3
8:4 3 2 1
total:8
比如：n = 6n=6，输出形式如下；
1:1 4 3 2 5 6
2:1 6 5 2 3 4
3:2 3 4 1 6 5
4:2 5 6 1 4 3
5:3 2 5 6 1 4
6:3 4 1 6 5 2
7:4 1 6 5 2 3
8:4 3 2 5 6 1
9:5 2 3 4 1 6
10:5 6 1 4 3 2
11:6 1 4 3 2 5
12:6 5 2 3 4 1
total:12

输入格式

一个整数 nn ；（2 \le n \le 102≤n≤10）

输出格式

前若干行，每行输出一个素数环的解，最后一行，输出解的总数。

输入输出样例

输入
4
输出
1:1 2 3 4
2:1 4 3 2
3:2 1 4 3
4:2 3 4 1
5:3 2 1 4
6:3 4 1 2
7:4 1 2 3
8:4 3 2 1
total:8

代码：

#include
using namespace std;
int n,b[20]={0},a[20],m=0;
int ok(int k,int i)//判断素数 
{int s,bj;if(k==1)return 1;s=a[k-1]+i;bj=1;for(int j=2;j<=int(sqrt(s));j++){ if(s%j==0){bj=0;break;}}if(k==n){//开头与结尾相连的情况 s=a[1]+i;for(int j=2;j<=int(sqrt(s));j++){if(s%j==0){bj=0;break;}		}}return bj;
}
void dfs(int k)
{int i;if(k==n+1){//输出 m++;cout<<m<<":";for(i=1;i<=n;i++)cout<<a[i]<<" ";cout<<endl;}else{for(i=1;i<=n;i++){if(!b[i]&&ok(k,i)){a[k]=i;b[i]=1;dfs(k+1);b[i]=0;}}} 
}
int main()
{cin>>n;dfs(1);cout<<"total:"<<m;return 0;
}

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！