Mathematics for Machine Learning学习笔记—3 解析几何

2023-11-24 15:26:50

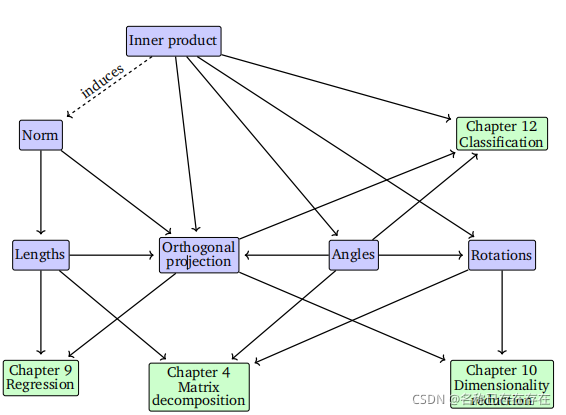
这一章主要讲了内积、范数、投影和正交化。几何向量的长度和角度。

3.1 Norms

几何向量（geometric vectors）是从原点开始的有向线段，向量的长度是“端”到原点的距离

范数（Norms)

Defifinition 3.1 (Norm) .在向量空间V中范数是 $\underset{x}{\rightarrow}$ 的长度，表示为 $\left | \left | \underset{x}{\rightarrow}\right | \right |$ 。性质： 1、 Absolutely homogeneous: $\left | \left | \lambda \underset{x}{\rightarrow} \right | \right |= \left | \lambda \right |\left | \left | \underset{x}{\rightarrow} \right | \right |$ 2、Triangle inequality: $\left \| \underset{x }{\rightarrow} +\underset{y}{\rightarrow}\right \|\leqslant \left \| \underset{x}{\rightarrow} \right \|+\left \| \underset{y}{\rightarrow} \right \|$ 3、Positive defifinite（正定性）： $\left \| \underset{x}{\rightarrow} \right \|\geqslant 0; \left \| \underset{x}{\rightarrow} \right \|= 0\Leftrightarrow \underset{x}{\rightarrow}=\underset{0}{\rightarrow}$ 范数分为 $l_{1}$ 范数、 $l_{2}$ 范数、 $l_{p}$ 范数、 $l_{\infty }$ 范数 $l_{1}$ 范数： $\left \| \underset{x}{\rightarrow} \right \|_{1}=\sum_{i=1}^{n}\left | x_{i} \right |$ $l_{2}$ 范数: $\left \| \underset{x}{\rightarrow} \right \|_{2}= \sqrt{\sum_{i=1}^{n}x_{i}^{2}}= \sqrt{\underset{x}{\rightarrow}^{T}\cdot \underset{x}{\rightarrow}}$

$l_{p}$ 范数: $\left \| \underset{x}{\rightarrow} \right \|_{p}= \sqrt[p]{\sum_{i=1}^{n}\left | x_{i} \right |^{p}}$

$l_{\infty }$ 范数: $\left \| \underset{x}{\rightarrow} \right \|_{\infty }=\max_{i\leqslant i\leqslant n}\left | x_{i} \right |$

3.2 Inner Products

内积（Inner Products）

一个向量的长度可以用内积表示，两个向量之间的角度和向量之间的距离也可以用内积表示。内积主要的目的是为了判断向量之间是否正交。

3.2.1 Dot Products

点积（Dot Products）:点积是内积的一种。

$\underset{x}{\rightarrow}^{T}\cdot \underset{y}{\rightarrow}= \sum_{i=1}^{n}x_{i}y_{i}$

3.2.2 General Inner Products

双线性映射 $\Omega$ ，向量空间V，向量 $\underset{x}{\rightarrow},\underset{y}{\rightarrow},\underset{z}{\rightarrow}\in V$ , $\lambda ,\psi \in R$ , 满足：

$\Omega \left ( \lambda \underset{x}{\rightarrow} +\psi \underset{y}{\rightarrow},\underset{z}{\rightarrow}\right )=\lambda \Omega \left ( \underset{x}{\rightarrow},\underset{z}{\rightarrow} \right )+\psi \Omega \left ( \underset{y}{\rightarrow} ,\underset{z}{\rightarrow}\right )$

$\Omega \left (\underset{x}{\rightarrow} ,\lambda \underset{y}{\rightarrow} +\psi \underset{z}{\rightarrow}\right )=\lambda \Omega \left ( \underset{x}{\rightarrow},\underset{y}{\rightarrow} \right )+\psi \Omega \left ( \underset{x}{\rightarrow} ,\underset{z}{\rightarrow}\right )$

Defifinition 3.2. 1.若对 $\forall$ $\underset{x}{\rightarrow},\underset{y}{\rightarrow}\in V$ ，V是一维空间 $\Omega \left ( \underset{x}{\rightarrow},\underset{y}{\rightarrow} \right )=\Omega \left ( \underset{y}{\rightarrow} ,\underset{x}{\rightarrow}\right )$ ，则称 $\Omega$ 是对称的（ symmetric）

2.若对 $\forall \underset{x}{\rightarrow}\in V and \underset{x}{\rightarrow}\neq \underset{0}{\rightarrow}$ , $\Omega \left ( \underset{x}{\rightarrow},\underset{x}{\rightarrow} \right )> 0$ , $\Omega \left ( \underset{0}{\rightarrow} ,\underset{0}{\rightarrow}\right )=0$ , 则称 $\Omega$ 是正定的（positive defifinite）

Defifinition 3.3. 1.一个对称正定的双线性映射 $\Omega$ ，被叫做向量空间V上的内积，将内积 $\Omega\left ( \underset{x}{\rightarrow} ,\underset{y}{\rightarrow}\right )$ 写作 $\left \langle \underset{x}{\rightarrow},\underset{y}{\rightarrow} \right \rangle$ 2. $\left ( V,\left \langle \cdot ,\cdot \right \rangle \right )$ 叫做内积空间或者叫（实）带有内积的向量空间。如果是点积，则叫做欧几里得向量空间。在这本书里，作者将所有空间认作内积空间，将所有出现的内积作为点积来计算。 Example3.3（内积不是点积）作者在这部分证明了内积不是点积，举例在二维空间下，内积不是点积。

3.2.3 Symmetric, Positive Defifinite Matrices

对称正定矩阵（Symmetric, Positive Defifinite Matrices）由内积定义得到的，在机器学习中有重要的作用。

一个具有内积的n维向量空间V，向量空间V中的一组有序的基向量 $B=\left ( \underset{b_{1}}{\rightarrow} ,\cdots ,\underset{b_{n}}{\rightarrow}\right )$ ，向量空间中的向量 $\underset{x}{\rightarrow},\underset{y}{\rightarrow}\in V$ 可以由基向量线性表示， $\underset{x}{\rightarrow}=\sum_{i=1}^{n}\psi _{i}\underset{b_{i}}{\rightarrow}$ ， $\underset{y}{\rightarrow}=\sum_{j=1}^{n}\lambda _{j}\underset{b_{j}}{\rightarrow}$ ，根据内积的双线性，对all $\underset{x}{\rightarrow},\underset{y}{\rightarrow}\in V$ 都有：

$\left \langle \underset{x}{\rightarrow} ,\underset{y}{\rightarrow}\right \rangle=\left \langle \sum_{i=1}^{n} \psi _{i}\underset{b_{i}}{\rightarrow},\sum_{j=1}^{n}\lambda _{j}\underset{b_{j}}{\rightarrow}\right \rangle=\sum_{i=1}^{n}\sum_{j=1}^{n}\varphi _{i}\left \langle \underset{b_{i}}{\rightarrow},\underset{b_{j}}{\rightarrow} \right \rangle\lambda _{j}=\hat{\underset{x}{\rightarrow}}^{T}A\hat{\underset{y}{\rightarrow}}$

内积<·,·>由A唯一确定，内积是对称的，意味着A也是对称的。

Defifinition 3.4 当 $\forall \underset{x}{\rightarrow}\in V and\underset{x}{\rightarrow}\neq \underset{0}{\rightarrow}$ ， $\underset{x}{\rightarrow}^{T}A\underset{x}{\rightarrow} > 0$ ，A被称为对称正定矩阵或者正定矩阵；若 $\underset{x}{\rightarrow}^{T}A\underset{x}{\rightarrow} \geqslant 0$ ，则A被称为对称半正定矩阵。

3.3 Lengths and Distances

将内积当作点积的时候，内积可以诱导出二范数。

Definition 3.6 （距离和矩阵） $\underset{x}{\rightarrow} and\underset{y}{\rightarrow}$ 的距离 $d\left ( \underset{x}{\rightarrow},\underset{y}{\rightarrow} \right ):=\left \| \underset{x}{\rightarrow} -\underset{y}{\rightarrow}\right \|=\sqrt{\left \langle \underset{x}{\rightarrow} -\underset{y}{\rightarrow},\underset{x}{\rightarrow} -\underset{y}{\rightarrow}\right \rangle}$

3.4 Angles and Orthogonality

Orthogonality（正交性）

orthogonal（正交的）

orthonormal（正交规范）

两个向量 $\underset{x}{\rightarrow},\underset{y}{\rightarrow}$ 之间的角度w： $cos\omega =\frac{\left \langle \underset{x}{\rightarrow} ,\underset{y}{\rightarrow}\right \rangle}{\left \| \underset{x}{\rightarrow}\right \|_{2}\left \| \underset{y}{\rightarrow} \right \|_{2}}=\frac{\left \langle \underset{x}{\rightarrow} ,\underset{y}{\rightarrow}\right \rangle}{\sqrt{\left \langle \underset{x}{\rightarrow} ,\underset{x}{\rightarrow}\right \rangle\left \langle \underset{y}{\rightarrow} ,\underset{y}{\rightarrow}\right \rangle}}=\frac{\underset{x}{\rightarrow}^{T}\underset{y}{\rightarrow}}{\sqrt{\underset{x}{\rightarrow}^{T}\underset{x}{\rightarrow}\underset{y}{\rightarrow}^{T}\underset{y}{\rightarrow}}}$

Definition3.7(正交性)当且仅当 $\left \langle \underset{x}{\rightarrow},\underset{y}{\rightarrow} \right \rangle$ =0，两向量正交。若向量 $\underset{x}{\rightarrow},\underset{y}{\rightarrow}$ 正交，且 $\left \| \underset{x}{\rightarrow} \right \|=\left \| \underset{y}{\rightarrow} \right \|=1$ ，则 $\underset{x}{\rightarrow},\underset{y}{\rightarrow}$ 是正交规范的（orthonoemal）。

若两个向量正交，则两向量垂直（当内积当作点积时）, 若内积不是点积，则两向量不垂直。Example3.7证明了这一点。

Definition 3.8(正交矩阵)正交矩阵的两种定义：

1. $A^{T}=A^{-1}$

2.方阵 $A_{n\times n}=\left [ \underset{\alpha _{1}}{\rightarrow} ,\cdots ,\underset{\alpha_{n }}{\rightarrow}\right ],\underset{\alpha _{i}}{\rightarrow}^{T}\underset{\alpha _{j}}{\rightarrow}=\left\{\begin{matrix} 0, i\neq j\\ 1,i=j \end{matrix}\right.$

矩阵是对象，一张数表存信息；矩阵是一种对向量操作的算子，有旋转和伸缩两种操作，A $\underset{x}{\rightarrow}$ ，表示A作用在 $\underset{x}{\rightarrow}$ 上，对 $\underset{x}{\rightarrow}$ 进行伸缩和旋转，但是当矩阵A固定时，对不同的向量的作用效果不一定相同。但是当A是正交矩阵时，矩阵A具有保长性和保角性。

保长性： $\left \| A\underset{x}{\rightarrow} \right \|_{2}=\left \| \underset{x}{\rightarrow} \right \|_{2}$

$\left \| A\underset{x}{\rightarrow} \right \|^{2}_{2}=\left ( A\underset{x}{\rightarrow} \right )^{T}\left ( A\underset{x}{\rightarrow} \right )=\underset{x}{\rightarrow}^{T}A^{T}A\underset{x}{\rightarrow}=\underset{x}{\rightarrow}^{T}I\underset{x}{\rightarrow}=\underset{x}{\rightarrow}^{T}\underset{x}{\rightarrow}=\left \| \underset{x}{\rightarrow} \right \|_{2}^{2}$ ，正交矩阵A对所有向量的伸缩比例都是1；

保角性：

$\small cos\omega =\frac{\left ( A\underset{x}{\rightarrow} \right )^T\left ( A\underset{y}{\rightarrow} \right )}{\left \| A\underset{x}{\rightarrow} \right \|\left \| A\underset{y}{\rightarrow} \right \|}= \frac{\underset{x}{\rightarrow}^{T}\underset{y}{\rightarrow}}{\sqrt{\left ( A\underset{x}{\rightarrow} \right )^{T}\left ( A\underset{x}{\rightarrow} \right )\left ( A\underset{y}{\rightarrow} \right )^{T}\left ( A\underset{y}{\rightarrow} \right )}}=\frac{\underset{x}{\rightarrow}^{T}\underset{y}{\rightarrow}}{\left \| \underset{x}{\rightarrow} \right \|\left \| \underset{y}{\rightarrow} \right \|}$

3.5 Orthonormal Basis

Orthonormal Basis(正交基)

Definition3.9（正交基）基向量的正交性： $\small \left \langle \underset{b_{i}}{\rightarrow},\underset{b_{j}}{\rightarrow} \right \rangle=\left\{\begin{matrix} 0,i\neq j\\ 1,i=j \end{matrix}\right.$

3.6 Orthogonal Complement

Orthogonal Complement(正交补)：两个子空间正交，三维空间中，过原点的平面和过原点的直线垂直。

3.7 Inner Product of Functions

函数的内积 $\small \left \langle u,v \right \rangle=\int_{a}^{b}u\left ( x \right )v\left ( x \right )dx$

3.8 Orthogonal Projections

3.9 Rotations

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！

标签：技术

上一篇 > 利用ChitGPT AI大模型生成解析几何介绍
下一篇 > 机器学习中的数学：（二）解析几何

Duilib中list控件支持ctrl和shif多行选中的实现

[ICML2015]Batch Normalization:Accelerating Deep Network Training by Reducing Internal Covariate Shif

win10系统微软输入法于eclipse ctrl+shif+f冲突间接处理办法

Codeforces Round #259 (Div. 2) B. Little Pony and Sort by Shif

读LDD3，内存映射与DMA--PAGE_SHIF…

VMware虚拟机安装XP【要先分区，再设置BOOT 启动CD，shif+上移】

更换iBus五笔的左与右Shif

sublime ctrl+shif+f 没用解决办法

idea 对 ctrl + z 的撤销是 ctrl + shif + z

计算机最早的设计师应用于,计算机应用基础选择题doc.doc

win10自带截图神器：Win+Shift+S

Python基础之文件目录操作

python简述目录_Python基础之文件目录操作(示例代码)

tp5 如何做数据采集

任务2-7(服务器字体+阿里巴巴矢量库)

html标签（1)：h1~h6,p,br,pre,hr

TI 电量计介绍与芯片选型指南

几款TI电源芯片简介

TI DSP芯片C2000系列读取FLASH数据

德州仪器(Ti)平台嵌入式开发基础

TI三相电机智能栅极驱动芯片特点分类

省选模拟（12.08） T3 圈圈圈圈圈圈圈圈

Hadoop生态圈技术栈（上）

大数据开发基础入门与项目实战（三）Hadoop核心及生态圈技术栈之6.Impala交互式查询

小猿圈之Linux下Mysql 操作命令

大数据Hadoop生态圈常用面试题

大数据开发基础入门与项目实战（三）Hadoop核心及生态圈技术栈之4.Hive DDL、DQL和数据操作

备战Noip2018模拟赛11（B组）T3 Monogatari 物语

【智能优化算法-圆圈搜索算法】基于圆圈搜索算法Circle Search Algorithm求解单目标优化问题附matlab代码

NYOJ 78 圈水池

递归问题跑道汽车绕圈问题 Python实现

Hadoop生态圈（三）：MapReduce