Cooperatively Coevolving Particle Swarms forLarge Scale Optimization
0、论文背景
该篇论文还是基于CPSO_Sk算法改正而来的,但是采用了CCSPO中随机分组技术,但是去掉了gbest前的权重搜索策略(效果虽然杠杠的,但是本身值得商榷),CCPSO2采用了一种新的PSO位置更新规则,依靠柯西分布和高斯分布对搜索空间中的新点进行采样,并提出了一种动态确定子空间维度大小的方案。
Li X, Yao X. Cooperatively coevolving particle swarms for large scale optimization[J]. IEEE Transactions on Evolutionary Computation, 2011, 16(2): 210-224.

1、CCPSO2
有关CCPSO、lbest PSO和CPSO参照:CCPSO、 lbest PSO、CPSO。
首先,我们采用了一个不使用速度项的PSO,而是使用 柯西分布和高斯分布来生成下一个粒子的位置。其次,我们 使用一个最佳环拓扑来定义每个粒子的局部邻域,以减缓收敛速度和保持更好的种群多样性。第三,而不是在随机分组机制的整个运行过程中使用固定的组(或子组件)大小,而是可以在 每次迭代中从一个集合中随机选择不同的组大小。1.1 柯西和基于高斯的PSO
由于GPSO只使用高斯分布,它探索搜索空间的能力相当有限,特别是当标准偏差σ变得非常小时,所以这里引入了柯西分布。
使用一个最佳环拓扑来定义每个粒子的局部邻域参见之前的博客lbest PSO。
1.2 动态更改组大小
定义一个S =[5, 10, 25, 50],每次的K值就是从中取一个。在每次迭代过程中,若全局最优值没有发生变化,那么K从这个集合中随机取一个作为子空间的维度。如果全局最优值发生变化K值沿用之前的值。
1.3 算法流程

2、算法实现
CPSO、CCPSO在之前的文章中都有实现过,这里不多加介绍,这里主要介绍CCPSO2的实现方式。在实验结果中,因为CCPSO采用了优化gbest前的权重,实验效果十分出色,值得以后算法的探讨。但是针对不优化gbest前的权重,那么CCPSO2相对于CPSO有多大的优势呢?
实验采用的是一个测试函数,评估次数都在20000次左右,重复实验100次取平均值。
function f = Rosenbrock(x)
% the Rosenbrock function
% xi = [-2.048,2.048]
f = sum(100*(x(:,2:end) - x(:,1:end-1).^2).^2 + (x(:,1:end-1)-1).^2,2);
endclc;clear;clearvars;
% 随机生成10个数据
num_initial = 10;
num_vari = 100;
% 搜索区间
upper_bound = 2.048;
lower_bound = -2.048;
% 迭代时计算y值总的个数
eval_num = 20000;
% K表示划分子空间的个数,sub_num表示每个子空间的维度;k表示领域大小。
S = [5, 10, 25, 50];
K = S(randi(4));
k = 2;
sub_num = num_vari / K;
% 算法的迭代次数,平均子空间的个数为90 / 4 = 22。
K1 = 20;
iter = eval_num / K1;
w = 1;
% 随机生成20个数据,并获得其评估值
sample_x = lhsdesign(num_initial, num_vari).*(upper_bound - lower_bound) + lower_bound.*ones(num_initial, num_vari);
sample_y = Rosenbrock(sample_x);
Fmin = zeros(iter, 1);
aver_Fmin = zeros(iter, 1);for n = 1 : 100n3 = 1;% 初始化一些参数pbestx = sample_x;pbesty = sample_y;[fmin, gbest] = min(pbesty);global_best_x = pbestx(gbest, :);fprintf("n: %.4f\n", n);lbest = ones(num_initial, num_vari);x = zeros(num_initial, num_vari);for i = 1 : iterindex = randperm(num_vari);fming = fmin;for i1 = 1 : Kindex1 = 1;% 随机分组ind = index((1 + (i1 - 1) * sub_num) : i1 * sub_num);r = rand(num_initial, sub_num);% pso更新下一步的位置,这里可以设置一下超过搜索范围的就设置为边界,服从自由度为1的t分布就是柯西分布if r > 0.5x(:, ind) = lbest(:, ind) + normrnd(0,1) .* abs(pbestx(:, ind) - lbest(:, ind));elsex(:, ind) = pbestx(:, ind) + trnd(1) .* abs(pbestx(:, ind) - lbest(:, ind));endx1 = x(:, ind);x1(x1 > upper_bound) = upper_bound;x1(x1 < lower_bound) = lower_bound;x(:, ind) = x1;x2 = repmat(global_best_x, num_initial, 1);x2(:, ind) = x1;y = Rosenbrock(x2);% 更新每个单独个体最佳位置pbestx1 = pbestx(:, ind);pbestx1(y < pbesty, :) = x1(y < pbesty, :);pbestx(:, ind) = pbestx1;pbesty(y < pbesty, :) = y(y < pbesty, :);% 更新每个个体的lbestn1 = ceil(k / 2);n2 = floor(k / 2);% 处理开头部分for i2 = 1 : n1[~, ind1] = min(pbesty(1 : (1 + k), 1));lbest(index1, ind) = pbestx(ind1, ind);index1 = index1 + 1;end% 处理中间部分for i3 = 1 : (num_initial - k)[~, ind2] = min(pbesty(i2 : (i2 + k), 1));lbest(index1, ind) = pbestx(i2 + ind2 - 1, ind);index1 = index1 + 1;end% 处理结尾部分for i4 = 1 : n2[~, ind3] = min(pbesty((num_initial - k) : num_initial, 1));lbest(index1, ind) = pbestx(num_initial - k + ind3 - 1, ind);index1 = index1 + 1;end% 更新所有个体最佳位置[fmin, gbest] = min(pbesty);global_best_x = pbestx(gbest, :);%fprintf("iter %d fmin: %.4f\n", i, fmin);endif fming == fminK = S(randi(4));sub_num = num_vari / K;endFmin(n3, 1) = fmin;n3 = n3 + 1;endaver_Fmin = aver_Fmin + Fmin;
end
aver_Fmin = aver_Fmin ./ 100;
plot(aver_Fmin);CCPSO2的结果:
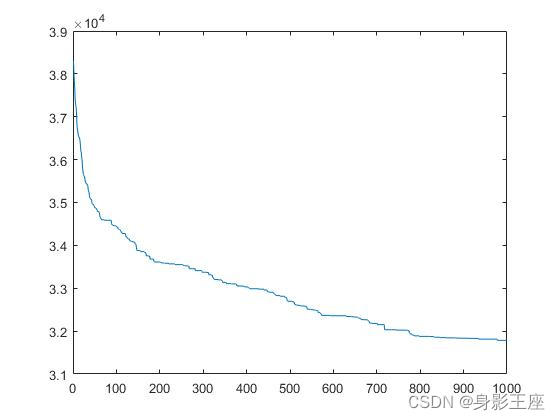
相同条件下,CPSO_Sk的结果
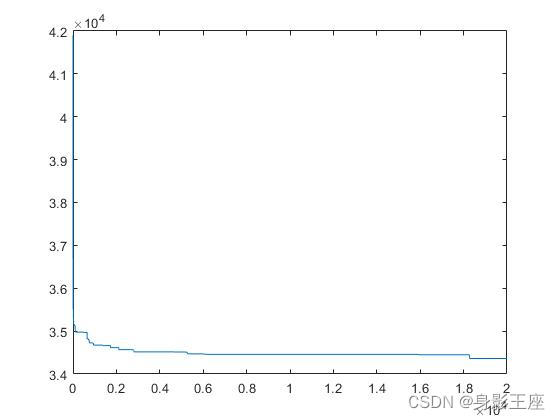
CCPSO由于用到了权重优化,效果过于显著,但是合理性以及科学性还需要论证:
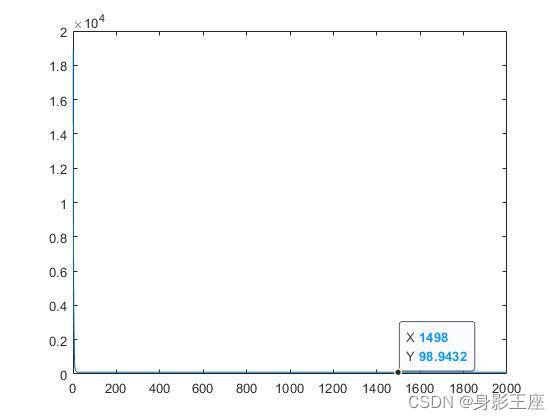
综上所述,CCPSO2在采用了随机分组技术、以及新的PSO位置更新规则,依靠柯西分布和高斯分布对搜索空间中的新点进行采样,并提出了一种动态确定子空间维度大小的方案,比起CPSO_Sk还是有不小的进步。
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!