python 求反函数_逆累积分布函数，累积分布函数及python实现

今天再看论文的时候看到一个名词叫：inverse cumulative distribution function。

查了一下，大部分称其为逆累积分布函数，这个叫法着实让人难理解，在这里我们把它称之为概率密度函数的反函数。

这篇文章分为三部分，

1. 概率密度函数（Probability density function， PDF）
2. 累积分布函数（cumulative distribution function， CDF）
3. 逆累积分布函数（inverse cumulative distribution function， ICDF）

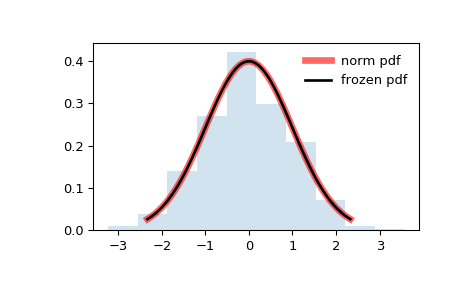
1 概率密度函数（Probability density function， PDF）

概率密度函数可以大致理解为，随着随机事件的改变，随机事件概率变化的程度。

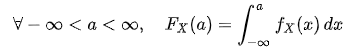
python 实现：

使用的是scipy库的stats模块。

import scipy.stats as st
print(st.norm.pdf(0) #求0处的概率密度值>>0.3989422804014327print(st.norm.pdf(0.8))
>>0.28969155276148273print(st.norm.pdf(-0.8))
>>0.28969155276148273
#符合标准正态分布的性质

2 累积分布函数（cumulative distribution function， CDF）

累积分布函数(Cumulative Distribution Function)，又叫分布函数，是概率密度函数的积分，能完整描述一个实随机变量X的概率分布。

定义如下：

并且在CDF可导的前提下，CDF的倒数 = PDF。

st.norm.cdf(0)
>>0.5st.norm.cdf(0.5)
>>0.6914624612740131st.norm.cdf(0.8)
>>0.7881446014166034st.norm.cdf(1)
>>0.8413447460685429st.norm.cdf(1.5)
>>0.9331927987311419#符合累积分布函数的性质，单调递增并趋向于1

3 逆累积分布函数（inverse cumulative distribution function， ICDF）

逆累积分布函数里面的"逆"，对应的英文单词是inverse
所以“逆累积分布函数”的意思其实是“反累积分布函数”累积分布：分位点－>概率，逆累积分布：概率－>分位点。

对于ICDF来说，是已知概率求分位点， 对于CDF来说，是已知分位点求概率。

分位点可理解为划分分布的一个点。

# ICDF 是 CDF的逆函数，所以我们用cdf组产生的实验结果
（0, 0.5） （0.5, 0.6914624612740131）（0.8, 0.7881446014166034）
（1, 0.8413447460685429 ）（1, 0.9331927987311419）st.norm.ppf(0.5)
>>0.0st.norm.ppf(0.6914624612740131)
>>0.5st.norm.ppf(0.7881446014166034)
>>0.8st.norm.ppf(0.8413447460685429)
>>1.0st.norm.ppf(0.8413447460685429)
>>1.4999999999999996

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！