计算机图形学笔记四：光栅化（抗锯齿，反走样）

光栅化（抗锯齿，反走样）

• 1.认识采样（Sampling）
• • 1.1什么是锯齿？
  • 1.2实际中的采样
  • 1.3采样错误的类型
• 2.认识走样（Aliasing Error）
• • 2.1反走样基本思路
  • 2.2频域（Frequency Domain）
  • • 2.2.1傅里叶变换（Fourier Transform）**
    • 2.2.2走样（Aliases）
  • 2.3滤波（Filtering）
  • • 2.3.1滤波=卷积（=平均值）
    • 2.3.2卷积的具体操作
    • 2.3.4采样=重复频率内容
    • 2.3.5走样的频域表示
• 3.减少走样
• • 3.1提高采样率
  • 3.2反走样（先模糊，后采样）
  • 3.3超采样抗锯齿（MSAA）
  • 3.4其他反走样方法

1.认识采样（Sampling）

1.1什么是锯齿？

首先通过上节我们可以知道，光栅化的采样就是判断像素点是否在三角形内部，最终对在内部的像素进行上色填充：

很明显，处理后的图形与我们原本的图形相差较大，这种现象就叫做锯齿现象，学名叫做“走样”（Alisaing）。而我们要解决的正是消除或缓解锯齿的出现。这个过程叫做“反走样”，或者成为“抗锯齿”。

1.2实际中的采样

把连续信号转换成离散信号的过程称为采样过程（sampling process）

1）光栅化=采样二维位置（Rasterization = Sample 2D Positions）

2）图片 = 对图像传感器平面进行采样（Photograph = Sample Image Sensor Plane）

3）视频=在时间上进行采样（Video = Sample Time）

1.3采样错误的类型

Sampling Artifacts (Errors / Mistakes / Inaccuracies) in Computer Graphics
1）锯齿样：
这也是“混叠”的一个例子——采样错误

2）摩尔纹
采样时跳过了图像中的奇数行和奇数列
手机拍电视

3）车轮效应
高速看车轮转动感觉像是逆时针转

2.认识走样（Aliasing Error）

首先要记住：走样=混叠错误，走样的英语（Aliasing Error）就是混叠错误的意思。

2.1反走样基本思路

基本思路：在做采样之前，先对原始的函数或信号做一个模糊处理（预过滤）Blurring (Pre-Filtering) Before Sampling
不做模糊处理：

请注意栅格化三角形中的锯齿，其中像素值为纯红色或白色。
模糊处理后：

请注意栅格化三角形中的抗锯齿边，其中像素值取中间值。
模糊处理后，再进行采样很明显，可以看出采样点数增加了，因此会更加逼近原图像。并且可以看到边界的点颜色教浅，并且越往外部去越浅，这样就会得到一种更加平滑的效果，不会像之前的锯齿那样变化锐利。
前面提到的图片进行反走样后，就会变成如下效果，可见抗锯齿效果还是很明显的。

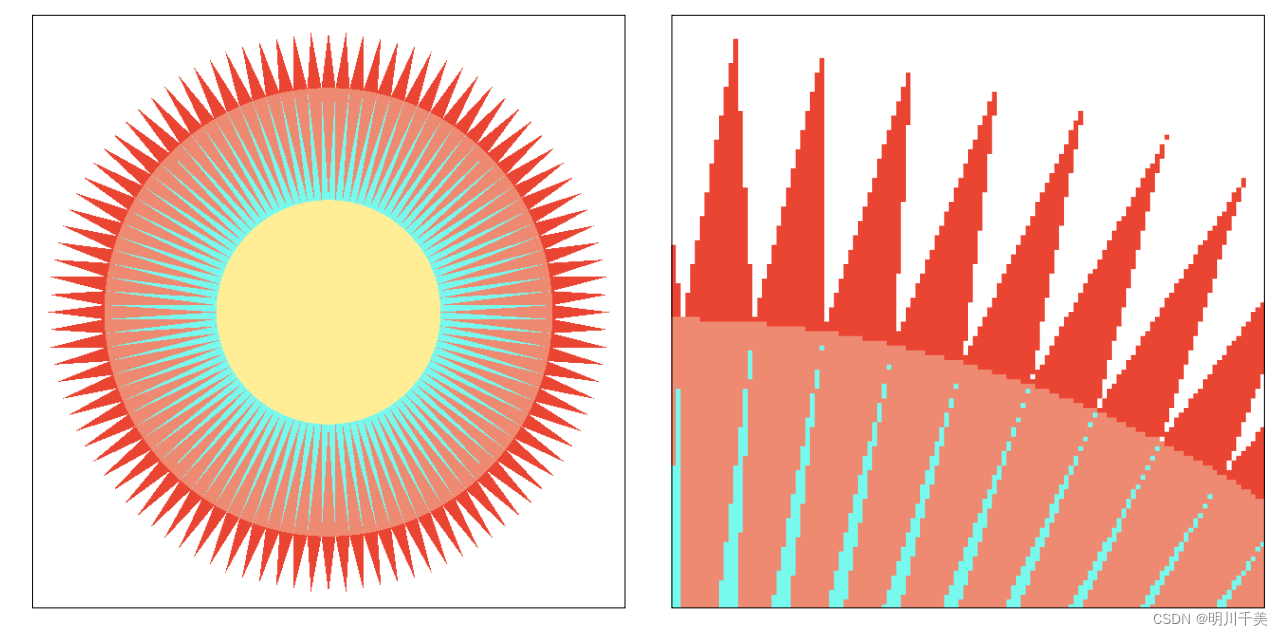
下面左图为直接采样，右图为先模糊后采样的效果：

如果先采样后模糊会是什么效果呢？
左图为先采样后模糊，右图为先模糊后采样。

可见，这样的效果并达不到我们想要的抗锯齿效果。
因此，我们现在主要解决两个问题：
1）为什么采样不足会出现锯齿
2）为什么先模糊后采样能够抗锯齿，而先采样后模糊不行？

2.2频域（Frequency Domain）

频域：频域是描述信号在频率方面特性时用到的一种坐标系。自变量是频率,即横轴是频率,纵轴是该频率信号的幅度,也就是通常说的频谱图。
例如：

可以看出不同系数的余弦波不同，主要是因为它们的频率（Frequencies）不同。频率越高，变化越快。

2.2.1傅里叶变换（Fourier Transform）**

傅里叶级数：一个函数$f(x)$，能够分解成许多不同的正弦波或者余弦波的和。
例如：

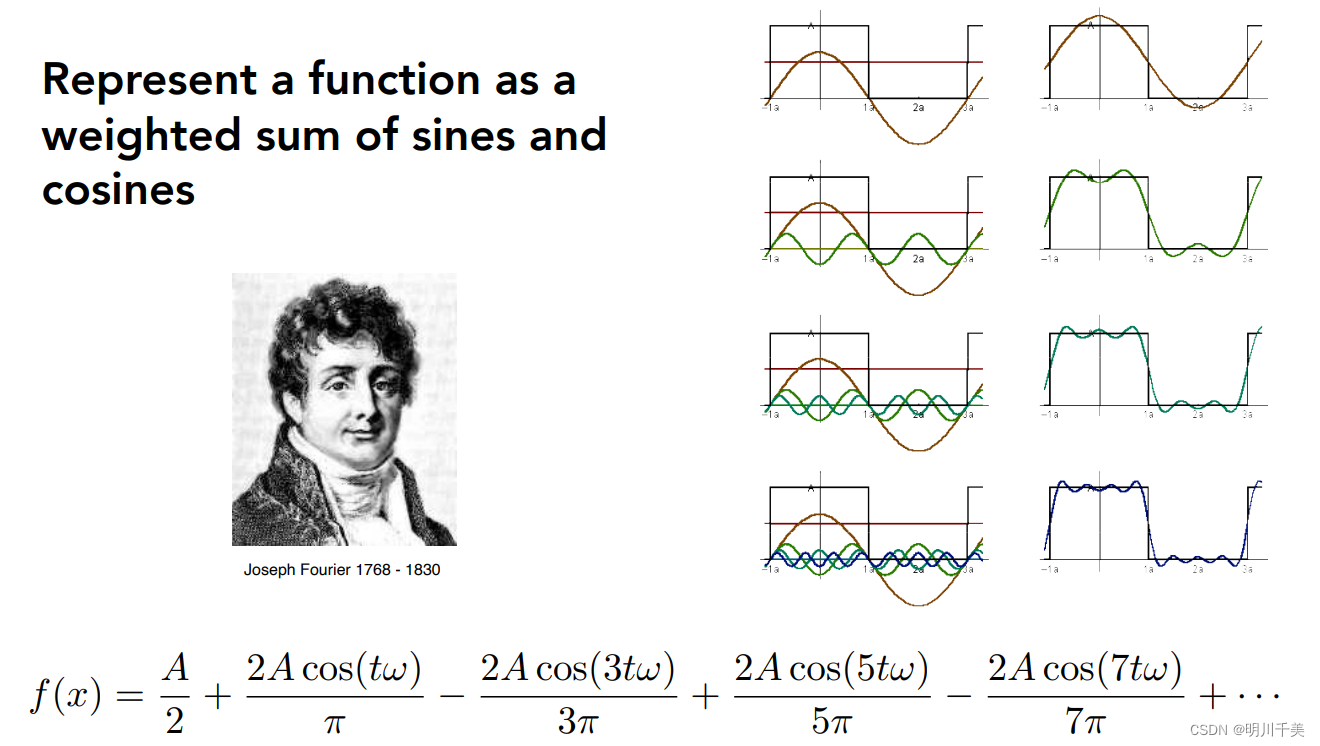
傅里叶变换的作用：将信号分解为频率，即将信号从时域转换到频域。（时域并不是说就一定是时间的信息。图像并不带任何时间的信息，但我们认为空间上的信息也算是时域，时域只是一个单纯的名字。这里指把图像从图像的空间变换到频率的空间）。

在上图中，左边的$f(x)$经过一系列的复杂变化（具体怎么变化，这里不考虑）可以变成右边的$F(x)$。即（时域→频域）。
同理，右边的$F(x)$也可以经过一系列的复杂变化（具体怎么变化，这里不考虑）可以变成左边的$f(x)$。即（频域→时域）。

2.2.2走样（Aliases）

如下图所示，接着将$f(x)$分解为5个函数，它们各有各自的频率，从上到下函数频率逐渐增高。

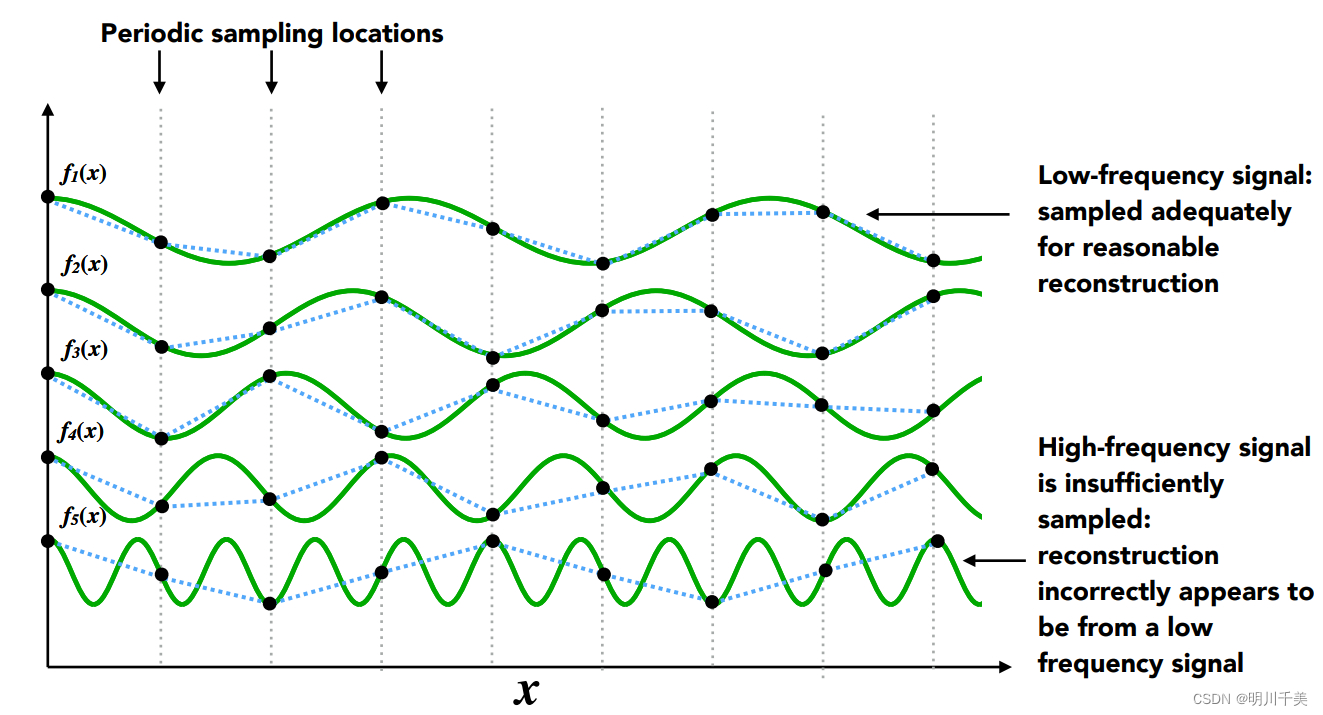
其中黑色虚线为采样位置，蓝色虚线为采样点连接后的新图像。很明显，上面频率低的函数图像采样后还算接近原图像，但下面频率高的已经与原图像相差甚远了。
相对应的，采样也是有一定的频率的，如果采样频率小于函数变化的频率，那么采样效果就好；反之，如果采样频率大于函数变化的频率，那么采样出的效果图就会与原函数很大不一样，造成采样错误。

再如通过频率解释什么是走样：

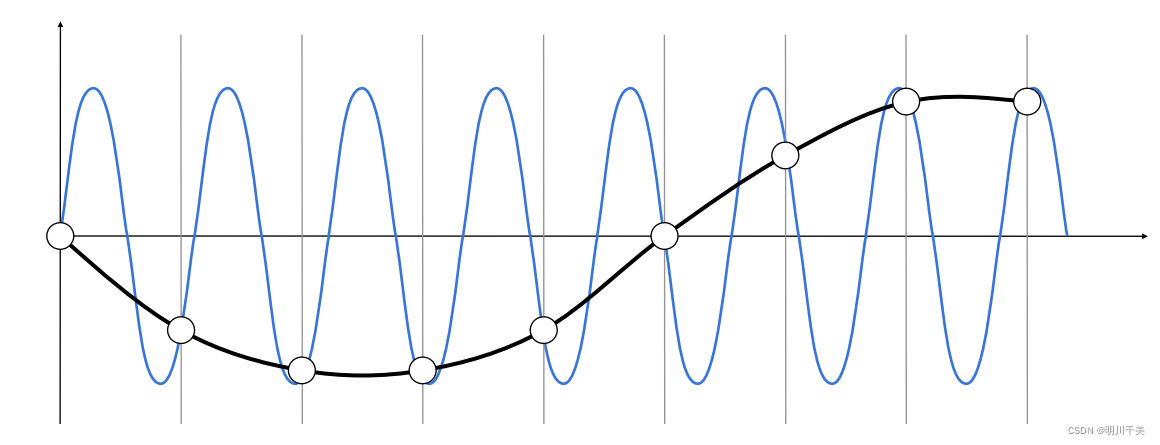
由图可以看出，当对蓝色函数进行采样时，采样结果是黑色线；当对黑色函数进行采样时，采样结果也是黑色线。因此可以得出结论：使用同样的采样方法，采样频率不同的信号，得到的采样结果可能相同。
用同样的一个采样方法采样两种频率截然不同的信号，但是采样的结果却是完全相同的，这就是“走样”。

至此，走样已经了解完毕，接着了解边界模糊是怎么做的？

2.3滤波（Filtering）

滤波 = 扔掉特定频率的内容
Filtering = Getting rid of certain frequency contents
下图中，左边是原图，通过傅里叶变换（将时域转变为频域）可以得到右边的频域图，从中心到外围，频率由低到高。

1）高通滤波器
通过这么一种滤波器，可以让图片只剩下高频，若下图所示：

在某一个地方，附近突然发生了剧烈的变化，比如黑衣服和白背景交界的位置。这就相当于信号发生了剧烈的变化，这个信号就处在高频的位置

2）低通滤波器
通过这么一种滤波器，可以让图片只剩下高频，若下图所示：

低频反之，只去掉了边界处。

3）中通滤波器
滤除低频和高频

最高的频率去掉，低频去掉，留下了接近边界的部分

2.3.1滤波=卷积（=平均值）

Filtering = Convolution (= Averaging)
下图为卷积操作：

由图可以看出：卷积就是将filter（滤波器）与其所覆盖的三个signal（信号）数字做点乘，再将求到的结果写到中间的格子里。
卷积定理：函数卷积的傅立叶变换是函数傅立叶变换的乘积，反之也成立。
结合上时域和频域，那就是在时域上，如果需要对两个信号进行卷积，其实对应到两个信号各自频域上，是两个信号的乘积。
简单来说，就是：
时域上的两个信号的卷积=频域上两个信号的乘积
时域上的两个信号的乘积=频域上两个信号的卷积
综上，我们得到两种卷积操作方法：
Option 1: 用滤波器对图像做卷积操作；
Option 2：先把图像变换到频域上（傅里叶变换），然后将滤波器作用到频域上，然后让两者做乘积操作，最后把结果变换到时域上（逆傅里叶变换）。

2.3.2卷积的具体操作

Option 1：直接将图片在时域上与卷积核做乘积

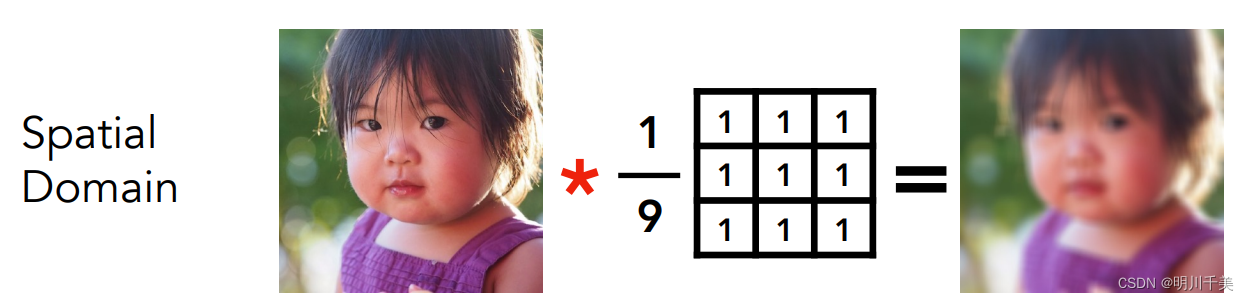
Option 2：

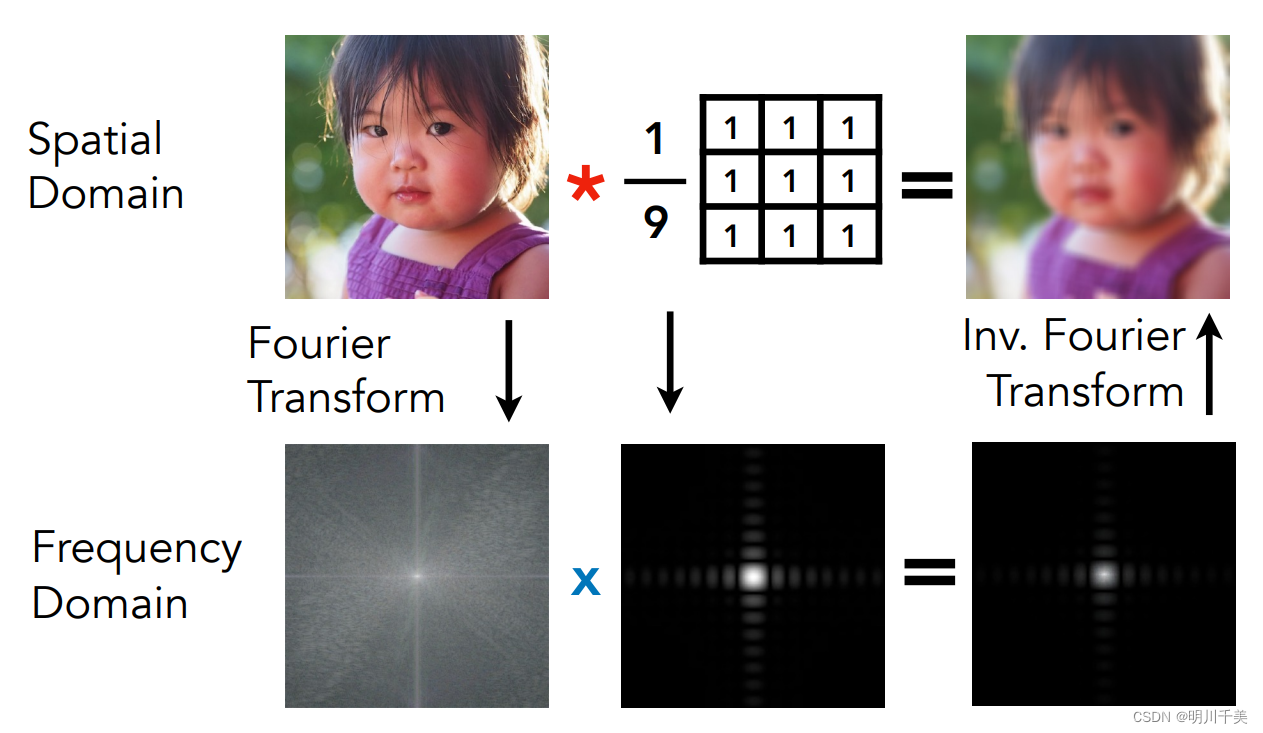
如上图所示，先将图像通过傅里叶变换转换到频域,得到一个频谱，再将卷积核通过傅里叶变换转换到频域，得到第二个频谱，然后将两个频谱做乘积，将最后得到的结果通过逆傅里叶变换转换到时域。得到的结果与方法一的相同。
注：
卷积核（Convolution kernel）：二维的矩阵
滤波器（Filter）：多个卷积核组成的三维矩阵，多出的一维是通道。（RGB三层通道）
一个“Kernel”更倾向于是2D的权重矩阵。而“filter”则是指多个Kernel堆叠的3D结构。如果是一个2D的filter，那么两者就是一样的。

卷积核就是求图像上某一点周围像素的平均值，然后将最后得到的结果作为中心点的像素，上图中取9个格子的平均数，所以要求为了不让图像变亮或者变暗，才取系数为1/9。

时域上的卷积核经过傅里叶变换之后在频域上的结果如下图所示：
左图为时域上,右图为频域上。

将卷积核变大后：

可以看出：卷积核越大，对应的频域越小。（越模糊）

2.3.4采样=重复频率内容

Sampling = Repeating Frequency Contents
左边为时域上，右边为频域上。

上图（b）是（a）经过傅里叶变换之后得到的频域上的图像,之所以为三角形是为了方便演示，不要在意其频谱是什么图形。
（c）是一个冲激函数，做（a）$\times$（c）的运算，可以得到结果（e），这就是对（a）进行的采样结果。
再看右边，根据时域上的乘积= 频域上的卷积，所以右侧应进行（b）卷积（d）的计算。得到的（f）就是卷积的结果。
由图可以得出结论：在时域上对一个连续函数进行采样，而在频域上，则是对该连续函数的频谱进行了一个复制粘贴的操作。

所以说：采样就是重复一个原始信号的频谱。也就是说在时域上进行采样 等价于 在频域上进行周期延拓。

2.3.5走样的频域表示

由图可以看出，采样的频率不够时，频谱的移动范围就会变小，最终导致频谱混叠。因此：走样=混叠错误，走样的英语（Aliasing Error）就是混叠错误的意思。

3.减少走样

3.1提高采样率

提升硬件水平，提高显示器分辨率。分辨率高，像素点多，采样率就高，采样也就密集了，走样就减少了。

3.2反走样（先模糊，后采样）

反走样=限制，然后重复。
Antialiasing = Limiting, then repeating

在采样之前，先用滤波器（虚线框）抹除掉高频率的信息，也就是通过滤波器先做一个模糊操作，砍掉高频，减少了频谱复制的面积。可见，这样采样后就不会发生走样（混叠错误）的现象了。

回到最开始：

先把高频信号去掉（边界去掉，用一定大小的低通滤波器进行卷积），得到模糊效果，然后进行采样。

3.3超采样抗锯齿（MSAA）

MSAA=Antialiasing By Supersampling
超采样抗锯齿是反走样的一个常用方法，就是模糊处理的方法。
在MSAA中,我们将以划分的每个像素再进行划分,将原有的一个像素分为更多个小像素。如下图,我们将原来的一个像素的区域又重新划分为了4*4 = 16 个像素的新区域.（一个像素内多加像素点）

原像素采样：

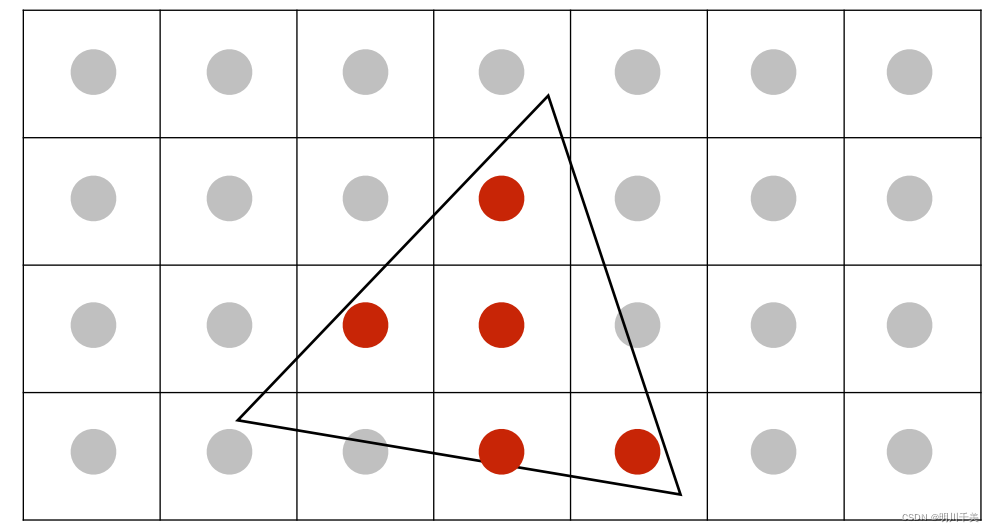
MSAA处理过程：
Step1：将的一个大像素分为多个个小像素

Step2：平均每个像素“内部”的采样数

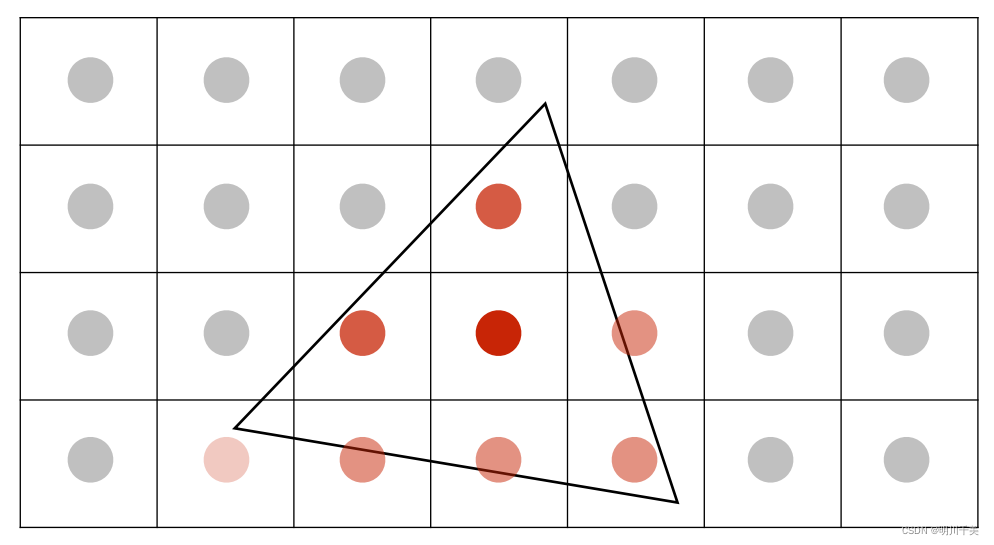
可以得出每个像素的覆盖结果:（相当于用卷积核对图像进行了一次卷积得到了模糊的效果）

MSAA缺点：增大计算量

3.4其他反走样方法

FXAA（Fast Approximate AA）：先得到有锯齿的图，从图像层面上，先将边界找到（通过图像匹配），然后将边界换成没有锯齿的边界。此方法与采样无关,是在图像处理的一种抗锯齿。速度很快。
TAA (Temporal AA)：对于静止的物品，复用上一帧感知的结果。

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！