sicp学习笔记1

第一章，构造过程抽象

define

define 2 size 解释器就会将size与2联系起来

ine

 前缀表达式

树形表示方法

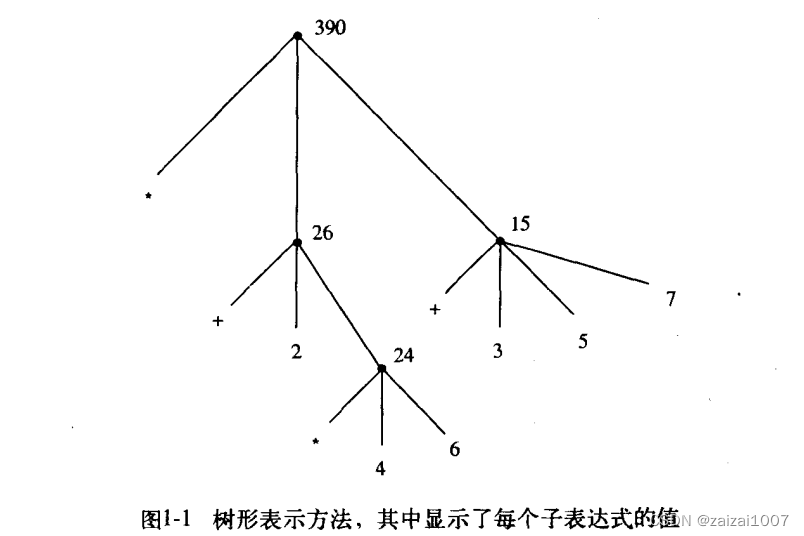
过程表达式

 square y == y*y  将过程和名称联系在了一起

正则表达式与应用表达式

应用式求值：

条件表达式和谓词 

 cond

 图中的表达式为求绝对值

这里首先包含一个符号 cond ，在它之后跟着一些称为子句的用括号括起来的表达式对偶(

) ,在每个对偶中的第一个表达式是一个 谓词 ，也就是说，这是一个表达式，它的值将被解释为真或假

and，or，not

( and (> x 5) (< x 10) ) 

 块结构

以下为求平方根的块

过程作为黑箱抽象

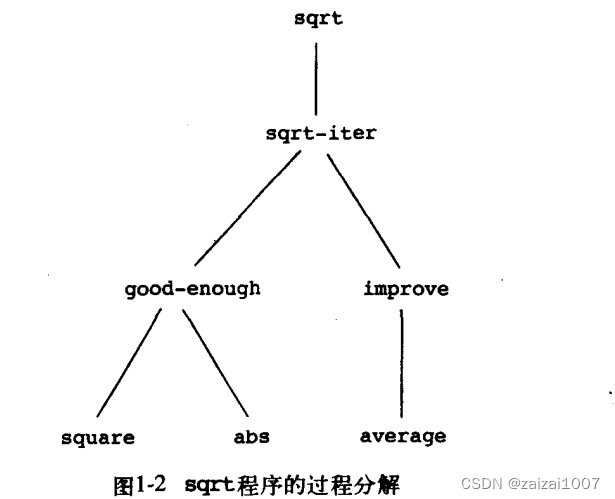
局部名 

过程用户不必去关心的实现细节之一

内部定义和块结构

将子过程直接定义在内部，避免了与外部的冲突

因为过程都定义在了块之内，所以 x 就变得自由了，不需要再传来传去，x 可以作为自由变量.在sqrt 被调用时，x由实际参数得到自己的值，这种方式称为 词法作用域 

过程与它们所产生的计算

树形递归

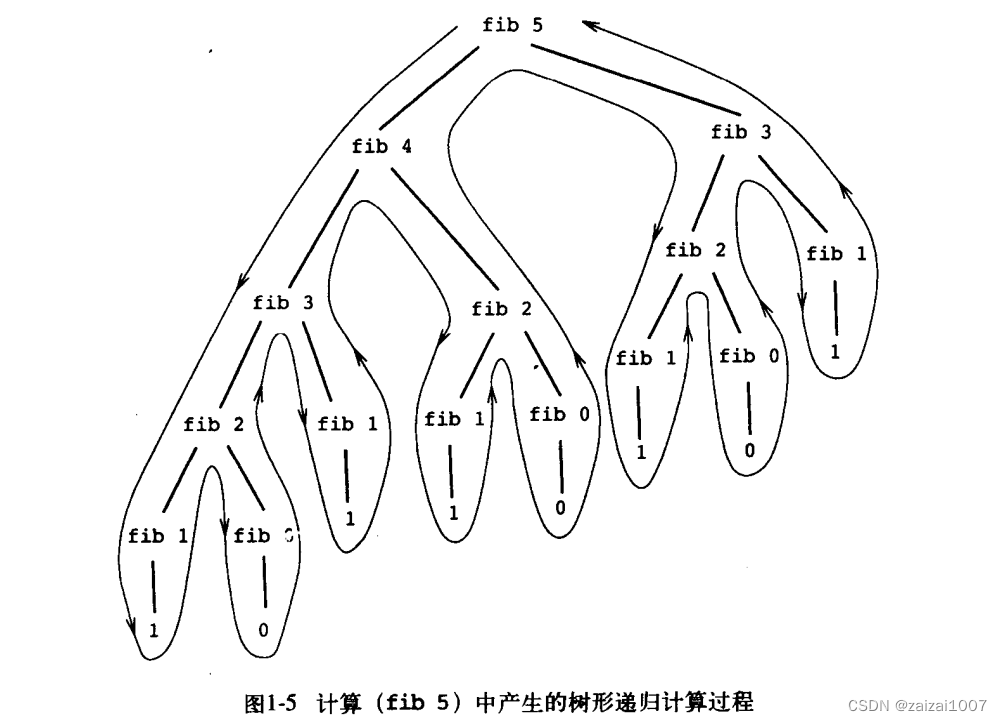
迭代法求斐波那契数列：

迭代法求：

(define (f n)(f-iter 2 1 0 0 n))(define (f-iter a b c i n)(if (= i n)c(f-iter (+ a (* 2 b) (* 3 c))   ; new aa                       ; new bb                       ; new c(+ i 1)n)))

增长的阶

 用高阶函数做抽象

过程作为参数

例子：

抽象出一个模板：

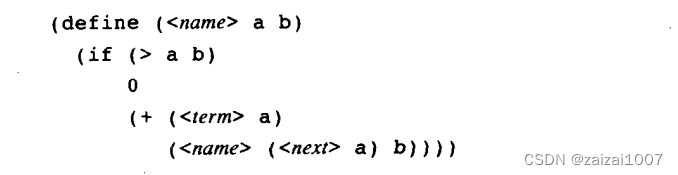
将空位翻译为形式参数：

 term 是一个过程参数,next 是a增长的过程参数

应用实例：

 实践：

(define (sum term a next b)(if (> a b)0(+ (term a)(sum term (next a) next b))))(define(simpson f a b n)(define h (/ (- b a) n))(define (y k)(f (+ a (* k h))))(define (factor k)(cond ((or (= k 0) (= k n))1)((odd? k)4)(else2)))(define (term k)(* (factor k)(y k)))(define (next k)(+ k 1))(if (not (even? n))(error "n can't be odd")(* (/ h 3)(sum term (exact->inexact 0) next n))))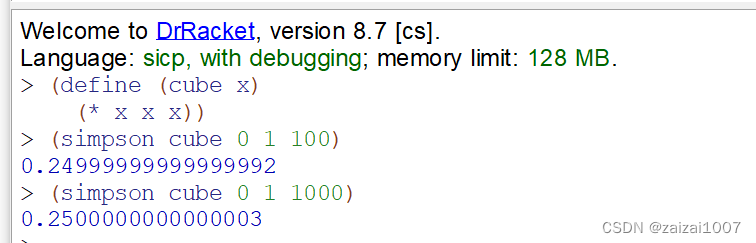

用 lambda 构造过程

可以直接将过程写进过程中，而不需要再定义辅助过程

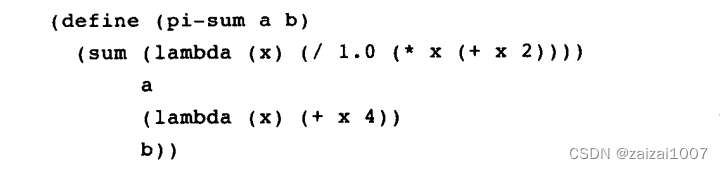
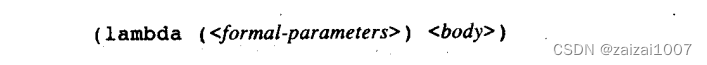
lambda 表达式可用作组合式的运算符

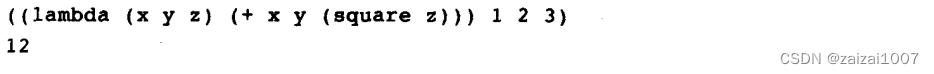
用 let 创建局部变量

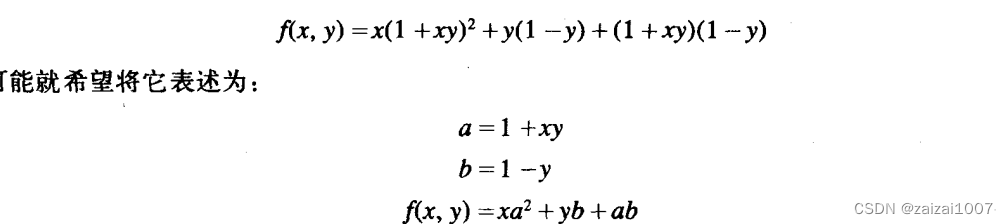
这样，解释器里就不需要为提供局部变量增加任何新机制。let  表达式只是作为其基础的lambda 表达式的语法外衣

过程作为一般性的方法

通过区间折半寻找方程的根

过程作为返回值

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！