数字图像处理考点分析（三）

频域图像增强

上一篇：数字图像处理考点分析（二） 我们介绍了空间域的图像增强的方法，下面我们将通过频率域滤波的方法来实现频率域的图像增强

文章目录

• • • • 频域图像增强
      • • 频率域滤波
        • 频率域滤波器
        • • 选择性滤波
          • 低通滤波器（频率域平滑滤波器）
          • 高通滤波器（频率域锐化滤波器）

Q: 既然有了空域增强的方法，为什么还需要频域增强的方法？

很多情况下，频率域滤波和空间域滤波可视为对于同一图像增强问题的殊途同归的两种解决方式。一些在空间域困难的增强任务，在频率域中变得非常普通。滤波在频率域更为直观，它可以解释空间域滤波 的某些性质。

傅里叶变换的频率分量和图像空间特征之间的联系

• 频率成分（u = v = 0）对应图像的平均灰度级。
• 当从变换的原点移开时，低频对应着图像的慢变化分量，如图像的平滑部分。
• 进一步离开原点时，较高的频率对应图像中变化越来越快的灰度级，如边缘或噪声等尖锐部分。

频率域滤波

频率域中的滤波技术是以如下处理为基础的：修改傅里叶变换以达到特殊目的，然后计算IDFT返回到图像域。
基本的滤波公式为：

g(x,y)=ζ^−1[H(u,v)F(u,v)]

其中ζ ^-1 是IDFT（离散傅里叶反变换），F(u,v)是输入图像f ( x , y ) f(x,y)f(x,y)的DFT（离散傅里叶变换），H(u,v)是滤波函数，g(x,y)是滤波后的（输出）图像。

频率域滤波的步骤

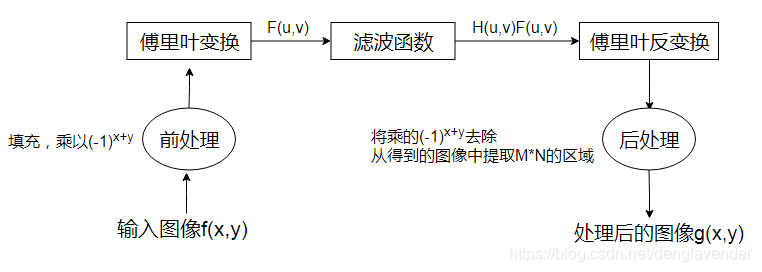
1. 给定一幅大小为MxN的输入图像f(x,y),选择填充参数P=2M.Q=2N；

2. 对f(x,y)添加必要数量的0，形成大小为PXQ的填充图像 fp(x,y)；

3. 用(−1)x+y乘以fp(x,y)，移到其变换中心；

4. 计算上图的DFT(离散傅里叶变换)，得到F(u,v)；

5. 生成一个实的，对称的滤波函数H(u,v)，其大小为PXQ，中心在(P/2,Q/2)处。用阵列相乘得到乘积G(u,v)=H(u,v)F(u,v)；即G(i,k)=H(i,k)F(i,k)；

   H和F的相乘在逐元素的基础上定义，即H的 第一个元素乘以F的第一个元素，H的第二个 元素乘以F的第二个元素。 一般，F的元素为复数，H的元素为实数。
   H为零相移滤波器，因为滤波器不改变变换的相位，F中实部和虚部的乘数(H)可以抵消。
   

6. 得到处理后的图像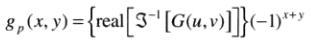：其中，为忽略由于计算不准确导致的寄生复成分，选择实部，下标p指出我们处理的是填充后的图像。

7. gp(x,y)的左上象限提取MxN区域，得到最终处理结果 g(x,y)

在频率域滤波的过程中，我们用到了DFT和IDFT（离散傅里叶逆变换）

一维情况下：

二维情况下：

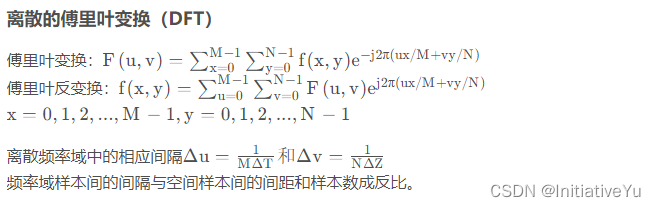
ps. H(u,v)称为滤波器。它在滤波中抑制或除去了频谱中的某些分量，而保留其他的一些频率不受影响，从而达到滤波的目的。类似于日常生活中的筛子，它可以严格按照尺寸使一些物体通过而同时阻止其他物体。

好了，知道了频域滤波的过程，我们现在需要做的就是根据不同的应用场景来算则不同的“筛子”

当然也就是选择合适的滤波函数H(u,v)！ 那下面我们就来看看有哪些频域滤波器，不同的的滤波器有不同的滤波函数，我们可以根据使用场景来选择不同的滤波器。

频率域滤波器

选择性滤波

常用的图像恢复方法有带阻滤波器、带通滤波器 、陷波滤波器等。
带阻滤波器：带阻滤波器消除或衰减了傅里叶变换原点附近的频段。
带通滤波器：带通滤波器执行与带阻滤波器相反的操作，可用全通滤波器减去带阻滤波器来实现带通滤波器。
陷波滤波器：陷波滤波器拒绝（或通过）事先定义的关于频率矩形中心的一个邻域的频率，可以选择性的修改DFT的局部区域

• 设置F(0,0)=0(结果图像的平均值为零)，而保留其 它傅里叶变换的频率成分不变。
• 除了原点处有凹陷外，其它均是常量函数。
• 由于图像平均值为0而产生整体平均灰度级的降低。
• 用于识别由特定的、局部化频域成分引起的空间图像 效果。

低通滤波器（频率域平滑滤波器）

使低频通过而使高频衰减的滤波器，被低通滤波的图像比原始图像少尖锐的细节部分而突出 平滑过渡部分。

对比空间域滤波的平滑处理，如均值滤波器

Q:低通滤波器为什么可以做到平滑处理？

• 边缘和噪声等尖锐变化处于傅里叶变换的高频部分
• 平滑可以通过衰减高频成分的范围来实现

分类

• 理想低通滤波器（ILPF）

  在以原点为圆心，以D0为半径的圆内，无衰减地通过所有频率，而在该圆外“阻断”所有频率的二维低通滤波，称为理想低通滤波器。由下述函数确定：

  

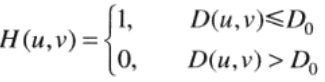
  D0是一个正常数，D(u,v)是频率域中，点(u,v)与频率矩形中心(0,0)的距离：

  

  

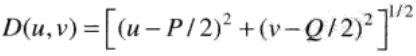
  理想低通滤波器的频率特性在截止频率处十分陡峭，无法用硬件实现，即其称之为理想的原因。

  小结：当截止频率非常低时，只有非常靠近原点的低频才能通过滤波器，得到的图像较模糊；截止频率越大，通过的频率越多，得到的图像越清晰。理想低通滤波器并不能很好的兼顾滤除噪声与保留细节两个方面。振铃现象是理想滤波器的一种特性。

  补充一下：图像处理中，对一幅图像进行滤波处理，若选用的频域滤波器具有陡峭的变化，则会使滤波图像产生“振铃”，所谓“振铃”，就是指输出图像的灰度剧烈变化处产生的震荡，就好像钟被敲击后产生的空气震荡。

• 巴特沃斯低通滤波器（BLPF）

  截止频率位于距原点D0处的n阶布特沃斯低通滤波器的传递函数定义为:

  

  

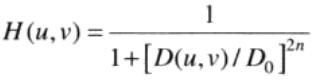
  应用：可用于平滑处理，如图像由于量化不足产生虚假轮廓 时，常可用低通滤波进行平滑以改进图像质量。通常，BLPF 的平滑效果好于ILPF（振铃现象）。

• 高斯低通滤波器（GLPF）

  二维高斯低通滤波器(GLPF)定义如下:

  

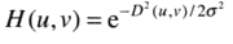
  D(u,v)是点(u,v)距原点的距离，使σ = D0（对应截止频率）

  

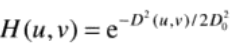
  当D(u,v)=D0时，滤波器下降到它最大值的0.607处

  

小结：

• GLPF不能达到有相同截止频率的二阶BLPF的平滑效果。
• GLPF没有振铃。
• 如果需要严格控制低频和高频之间截止频率的过渡， 选用BLPF，代价是可能产生振铃

高通滤波器（频率域锐化滤波器）

使高频通过而使低频衰减的滤波器,，被高通滤波的图像比原始图像少灰度级的平滑过渡而突出边缘等细节部分。

对比空间域的梯度算子、拉普拉斯算子

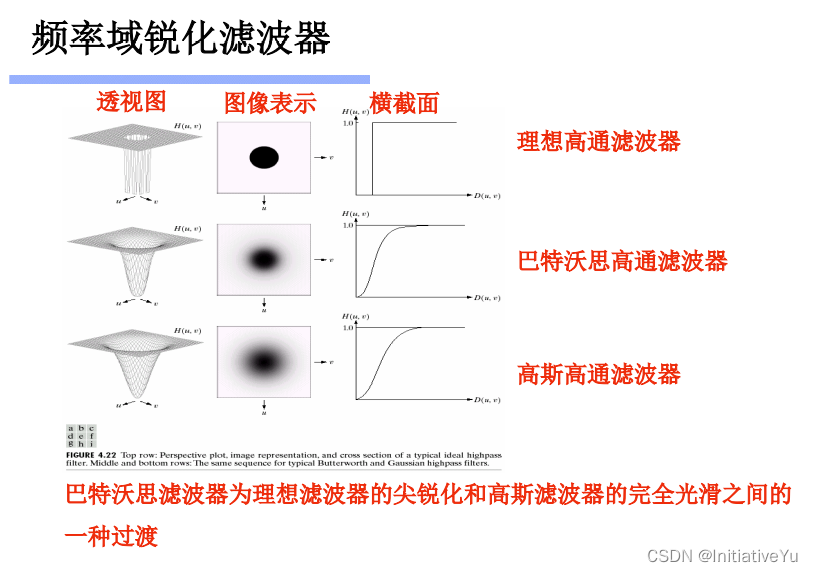
分类：

• 理想高通滤波器 （IHPF）

  截断傅里叶变换中的所有低频成分，这些低 频成分处于指定距离D0之内

  

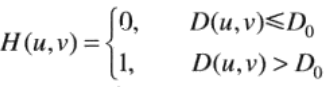
  频率矩形的中心在(u,v)=(P/2,Q/2)，从点 (u,v)到中心（原点）的距离如下:

  

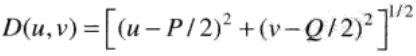
• 巴特沃思高通滤波器 （BHPF）

n阶且截至频率距原点的距离为D0的巴特沃 思高通滤波器(BHPF)定义为：

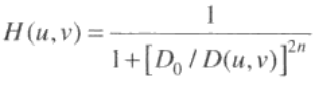
结论：BHPF的结果比IHPF的结果平滑得多

• 高斯高通滤波器

截频距原点为D0的高斯高通滤波器(GHPF)定 义为：

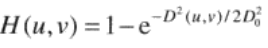
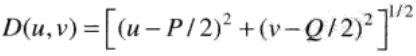
结论：GHPF的结果比BHBF和IHPF的结果更平滑

• 频率域的拉普拉斯算子

之前我们已经使用过拉普拉斯算子对空间域的图像进行增强。现在使用拉普拉斯算子在频率域对图像进行增强。频域的拉普拉斯滤波器由下述函数确定：

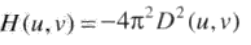
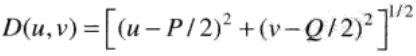
总结：

1. 随着D0的增大，低通滤波器的模糊水平降低，高通滤波器的锐化水平降低。
2. ILPF会产生振铃现象；与ILPF相比, BLPF变换传递函数比较平滑；GLPF图像边缘的模糊程度较BLPF产生的要大一些
3. IHPF通常具有振铃性质，微小物体和线条被加强，呈白色；BGPF比IHPF要平滑，边缘失真小；GHPF效果比BHPF稍弱，振铃现象不明显
4. 一阶BLPF没有振铃，二阶稍有但不明显
5. 高通滤波器让高频成分通过，使低频成分削弱，再经傅立叶逆变换得到边缘锐化的图像。Hhp(u,v)=1−Hlp(u,v)
6. 带通滤波使得图像的部分细节被突出

下一篇：数字图像处理考点分析（四） 我们将去学习图像复原技术!

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！