支持向量机SVM（一）

文章目录

• 1 概述
• 2 支持向量机分类器是如何工作的
• 3 线性SVM用于分类的原理
• • 3.1 线性SVM的损失函数详解
  • 3.2 线性SVM的拉格朗日对偶函数和决策函数
  • • 3.2.1将损失函数转换为拉格朗日乘数的形态
    • • 3.2.1.1为什么可以转换成拉格朗日函数？
      • 3.2.1.2为什么可以进行转换？
      • 3.2.1.3 怎样进行转换？
    • 3.2.2将拉格朗日转换成对偶函数
    • • 3.2.2.1 为什么要进行转换？
      • 3.2.2.2 为什么能够进行转换？
      • 3.2.2.3怎样转换？
  • 3.3 求解拉格朗日对偶函数极其后续过程
• 4 线性SVM决策过程的可视化
• 5 为非线性数据增加维度并绘制3D图像

1 概述

支持向量机（SVM，也称为支持向量网络），是机器学习中获得关注最多的算法没有之一。它源于统计学习理论，是我们除了集成算法之外，接触的第一个强学习器。它有多强呢？

从算法的功能来看，SVM几乎囊括了我们前六周讲解的所有算法的功能：

从分类效力来讲，SVM在无论线性还是非线性分类中，都是明星般的存在：

2 支持向量机分类器是如何工作的

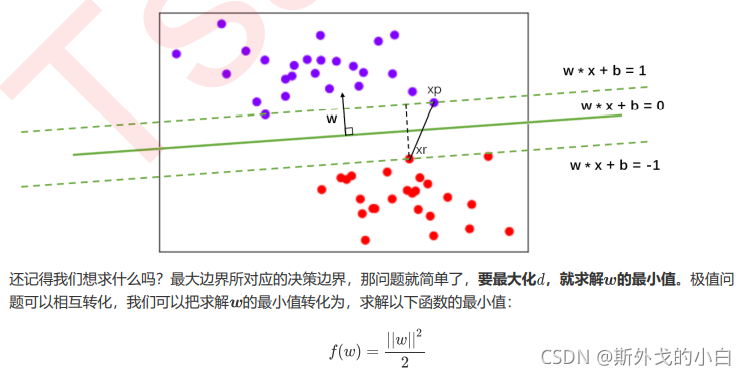
支持向量机的分类方法，是在这组分布中找出一个超平面作为决策边界，使模型在数据上的分类误差尽量接近于小，尤其是在未知数据集上的分类误差（泛化误差）尽量小。


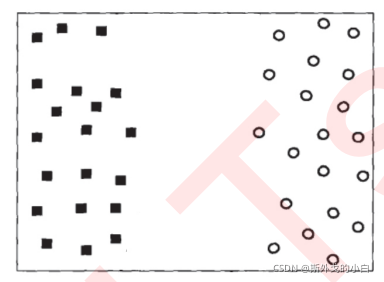
决策边界一侧的所有点在分类为属于一个类，而另一侧的所有点分类属于另一个类。如果我们能够找出决策边界，分类问题就可以变成探讨每个样本对于决策边界而言的相对位置。比如上面的数据分布，我们很容易就可以在方块和圆的中间画出一条线，并让所有落在直线左边的样本被分类为方块，在直线右边的样本被分类为圆。如果把数据当作我们的训练集，只要直线的一边只有一种类型的数据，就没有分类错误，我们的训练误差就会为0。但是，对于一个数据集来说，让训练误差为0的决策边界可以有无数条。

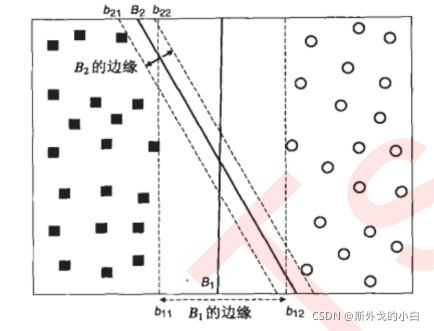
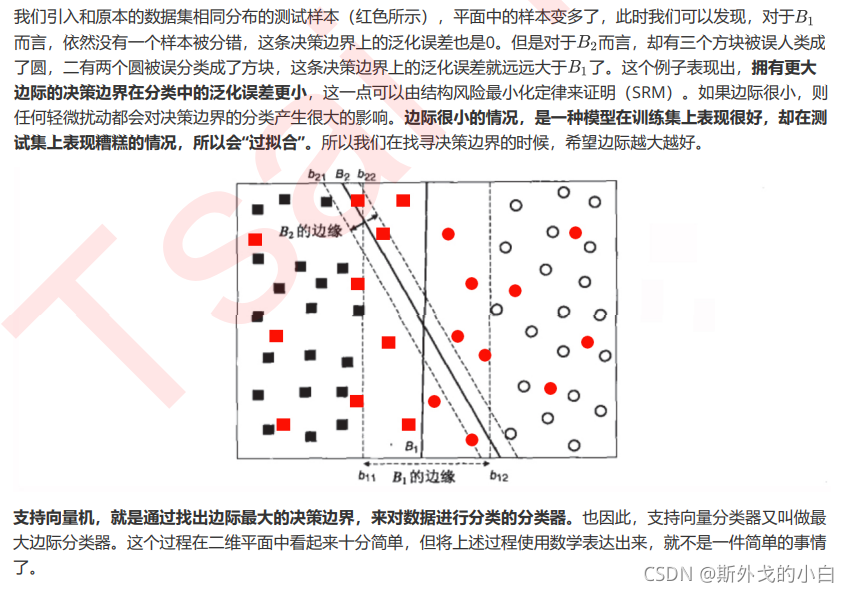
3 线性SVM用于分类的原理

3.1 线性SVM的损失函数详解

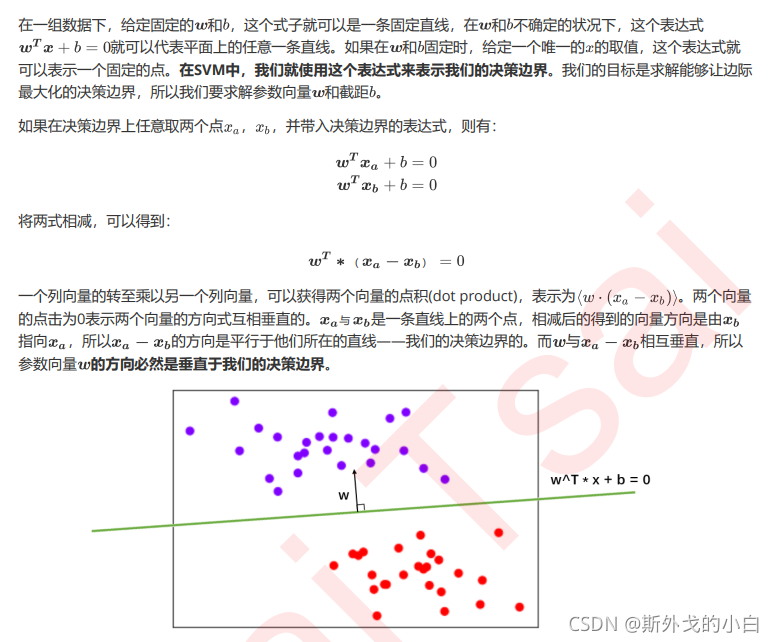
3.2 线性SVM的拉格朗日对偶函数和决策函数

3.2.1将损失函数转换为拉格朗日乘数的形态

3.2.1.1为什么可以转换成拉格朗日函数？

3.2.1.2为什么可以进行转换？

3.2.1.3 怎样进行转换？

3.2.2将拉格朗日转换成对偶函数

3.2.2.1 为什么要进行转换？

3.2.2.2 为什么能够进行转换？

3.2.2.3怎样转换？

3.3 求解拉格朗日对偶函数极其后续过程

4 线性SVM决策过程的可视化

from sklearn.datasets import make_blobs
from sklearn.svm import SVC
import matplotlib.pyplot as plt
import numpy as npx, y = make_blobs(n_samples=50, centers=2, random_state=0, cluster_std=0.6)
#print(x, y)#实例化数据集，可视化数据集plt.scatter(x[:, 0], x[:, 1], c=y, s=50, cmap="rainbow")
plt.xticks([])
plt.yticks([])
plt.show()

#画决策边界，理解函数counter
#首先要画散点图plt.scatter(x[:, 0], x[:, 1], c=y, s=50, cmap="rainbow")
ax = plt.gca()  #获取当前的子图，如果不存在，则创建新的子图#获取平面上两条坐标轴的最大值和最小值
xlim = ax.get_xlim()
#(-0.7503988002924934, 3.380032929005172)
ylim = ax.get_ylim()
#(-0.4292462471025815, 5.765392910228977)
#print(xlim, ylim)#在最大值和最小值之间形成30个规律的数据
axisx = np.linspace(xlim[0], xlim[1], 30)
axisy = np.linspace(ylim[0], ylim[1], 30)axisx, axisy = np.meshgrid(axisx, axisy)
#print(axisx.shape, axisy.shape)
#(30, 30) (30, 30) 这一步相当于从x轴和y轴分别找到30条线，然后让他们配对
#实质上,经过meshgrid之后呢，axisx是一个二维数组，一共30行，每行30个数据，每一行的数据分别是对应的x轴上划分的刻度值xy = np.vstack([axisx.ravel(), axisy.ravel()]).T
#print(xy.shape)
#(900, 2)
##其中ravel()是降维函数，vstack能够将多个结构一致的一维数组按行堆叠起来
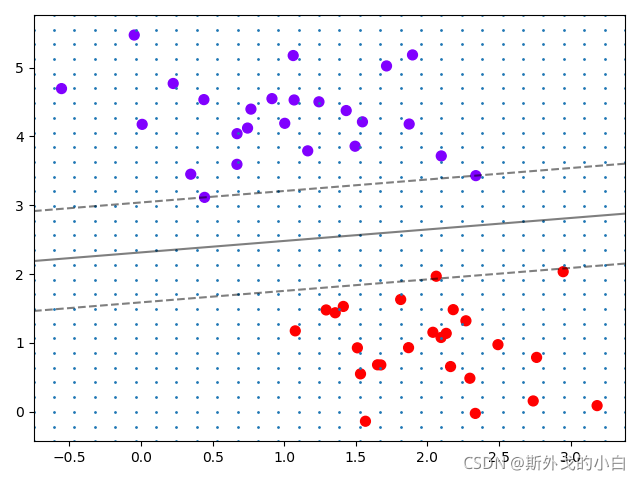
#xy就是已经形成的网格，它是遍布在整个画布上的密集的点plt.scatter(xy[:, 0], xy[:, 1], s=1, cmap="rainbow")
plt.show()

#建模，计算决策边界并找出网格上每个点到决策边界的距离
clf = SVC(kernel="linear").fit(x, y)
z = clf.decision_function(xy).reshape(axisx.shape)
#重要接口decision_function，返回每个输入的样本所对应的决策边界的距离
#然后再将这个距离转换为axisx的结构，这是由于画图的函数contour要求z的结构必须要axisx，axisy的结构一样#画决策边界和平行于决策边界的超平面
ax.contour(axisx, axisy, z, colors="k", levels=[-1, 0, 1], alpha=0.5, linestyles=["--", "-", "--"])
#把所有的点都放进来，把计算得到的距离都放进来，把等高线的高度放进来ax.set_xlim(xlim)
ax.set_ylim(ylim)
plt.show()

#print(x[10]) #[1.71444449 5.02521524]
#print(x[10].reshape(1, 2)) #[[1.71444449 5.02521524]]
plt.scatter(x[:, 0], x[:, 1], c=y, s=50, cmap="rainbow")
plt.scatter(x[10, 0], x[10, 1], c="black", s=50, cmap="rainbow")
clf.decision_function(x[10].reshape(1, 2))
plt.scatter(x[:, 0], x[:, 1], c=y, s=50, cmap="rainbow")
ax = plt.gca()
ax.contour(axisx, axisy, z, colors="k", levels=[-3.33917354], alpha=0.5, linestyles=["--"])
plt.show()

#将绘图过程包装秤函数
def plot_scv_decision_function(model, ax=None):if ax is None:ax = plt.gca()xlim = ax.get_xlim()yilm = ax.get_ylim()x = np.linspace(xlim[0], xlim[1], 30)y = np.linspace(ylim[0], ylim[1], 30)Y, X = np.meshgrid(y, x)xy = np.vstack([X.ravel(), Y.ravel()]).TP = model.decision_function(xy).reshape(X.shape)ax.contour(X, Y, P, colors="k", levels=[-1, 0, 1], alpha=0.5, linestyles=["--", "-", "--"])ax.set_xlim(xlim)ax.set_ylim(ylim)clf = SVC(kernel="linear").fit(x, y)
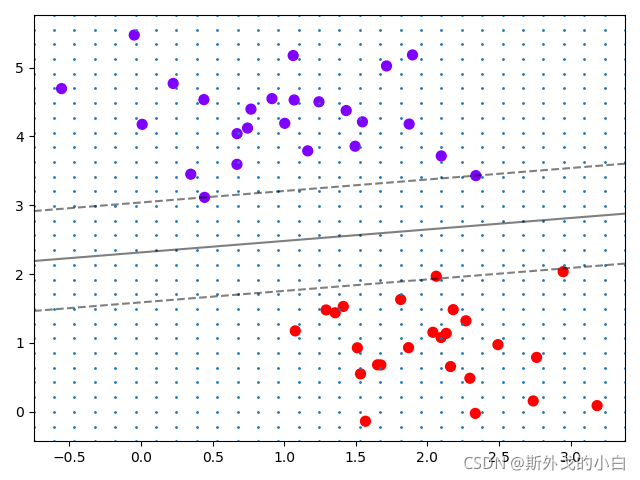
plt.scatter(x[:, 0], x[:, 1], c=y, s=50, cmap="rainbow")
plot_scv_decision_function(clf)
plt.show()

重要的接口

#探索建好的模型
print(clf.predict(x))
#根据决策边界，对x中的样本进行分类，返回的结构为n_samples[1 1 0 0 1 1 1 1 1 0 0 0 0 1 0 0 0 1 0 0 1 1 1 1 1 0 0 0 1 0 1 0 0 0 0 1 10 1 0 1 0 1 1 0 1 1 0 1 0]print(clf.score(x, y))
#返回给定测试数据和标签的平均准确度
1.0print(clf.support_vectors_)
#返回支持向量[[0.44359863 3.11530945][2.33812285 3.43116792][2.06156753 1.96918596]]print(clf.n_support_)
#返回每个类中的支持向量个数
[2 1]

5 为非线性数据增加维度并绘制3D图像

对于环形数据来说如何寻找超平面？

import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import make_circles
from mpl_toolkits import mplot3d
x, y = make_circles(100, factor=0.1, noise=0.1)
#print(x.shape)  #(100, 2)
#print(y.shape)  #(100,)#既然要兑换到三维，就需要建一个新的维度r
r = np.exp(-(x ** 2).sum(1))
rlim = np.linspace(min(r), max(r), 100)##定义一个绘制三维图像的函数
#elev表示上下旋转的角度
#azim表示平行旋转的角度
def plot_3D(elev=30, azim=30, x=x, y=y):ax = plt.subplot(projection="3d")ax.scatter3D(x[:, 0], x[:, 1], r, c=y, s=50, cmap="rainbow")ax.view_init(elev=elev, azim=azim)ax.set_xlabel("x")ax.set_ylabel("y")ax.set_zlabel("r")plt.show()plot_3D()

将二维图片转换到三维领域，由于x特征值不同，在更高维度中可以找到一个平面直接将两类数据进行切分！

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！