AI 人工智能之概率论基础(4)

后验概率

后验概率是指在得到“结果”的信息后重新修正的概率，是“执果寻因”问题中的"果"。先验概率与后验概率有不可分割的联系，后验概率的计算要以先验概率为基础。

后验概率的计算要以先验概率为基础。后验概率可以根据通过贝叶斯公式，用先验概率和似然函数计算出来。后验概率实际上就是条件概率。

先验概率是以全事件为背景下，A事件发生的概率：P(A|Ω)
后验概率是以新事件B为背景下，A事件发生的概率： P(A|B)
全事件一般是统计获得的，所以称为先验概率，没有实验前的概率
新事件一般是实验，如试验B，此时的事件背景从全事件变成了B，该事件B可能对A的概率有影响，那么需要对A现在的概率进行一个修正，从P(A|Ω)变成 P(A|B)，所以称 P(A|B)为后验概率，也就是试验(事件B发生)后的概率。

贝叶斯公式——后验概率的公式

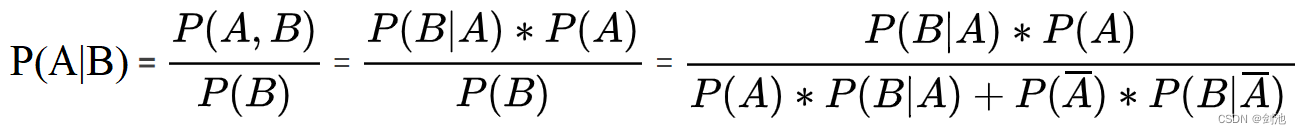
假设某个事件的结果为R的概率为P(R)，造成B的原因有事件1、2、3，事件1、2、3发生的概率分别为P(1)、P(2)、P(3)，事件1、2、3导致结果R发生的概率为P(R|1)、P(R|2)、P(R|3)，现在事件结果R发生了，问事件1发生的概率是多少？

P(R)=事件1发生并导致R+事件2发生并导致R+事件3发生并导致R，即：
P(R)=P(1,R)+P(2,R)+P(3,R)

事件1发生并导致R发生：
P(1,R)=P(1)*P(R|1)；

就是事件1发生的概率*事件1导致R发生的概率，同理：
P(2,R)=P(2)*P(R|2)；
P(3,R)=P(3)*P(R|3)；

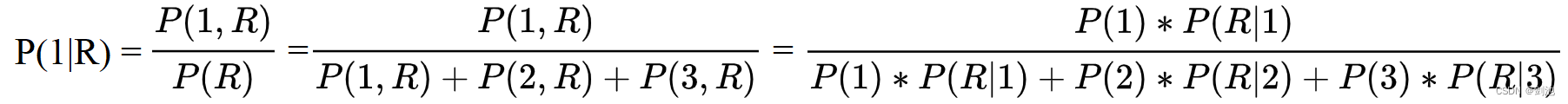
最大后验概率估计 

最大似然估计时，估计的是 P(x|)(P即f)。而最大后验概率估计，估计的是P(x|)P()，即将参数本身的概率也考虑进去，既希望概率最大，也希望参数自身先验概率也最大，相当于是一个期望更大值的正则项。

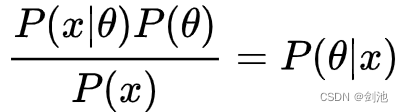 其中P(x)已知了，所以估计 P(x|)P()就是估计 P(|x)，即后验概率。在求解时可将 P()代入，同理求解最大值，得到得到最大后验概率估计。

作者：华为云开发者联盟
链接：https://www.zhihu.com/question/275624152/answer/2561712013
来源：知乎
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。
 

拼写纠正实例

假设你在手机里输入了tha，那么大概率不同手机的人所得到的单词不是一样的，即使你是使用相同的手机在相同的输入法中，也会得到不同的结果。

好，那么问题来了，为什么会这样呢？实际上这里有个叫用户习惯，它会将你经常使用的某个单词放在最显眼的位置，也就是放在第一个位置。这样听起来可能你会想到和概率统计有关，实际上还有另外一种，比如你是想输入the的，结果输入tha，那么软件该怎么判断呢？软件会想用户到底是需要输入什么单词呢？这里我们用到概率为P(猜测输入的单词|实际输入的单词)，比如就有P1=(the|tha) P2=(that|tha)…

假设用户实际输入的单词为W（W为观测数据）,猜测的单词为c

那么就会有P1(c1|W)，P2(c2|W)，P3(c3|W)…

统一为：P(c|W)

则根据贝叶斯公式可得：P(c|W)=P(c)*P(W|c)/P(W)

对于不同的具体猜测c1,c2,c3，我们可以知道P(W)都是一样的，所以在比较P(c1|W)和P(c2|W)时这个常数是可以忽略的。

P(c|W)和P(c)*P(W|c)是正相关

P(c)是指的先验概率，之前说贝叶斯函数的思想和普通函数的思想是有一定的不同的，对于给定的W，一个猜测是好是坏，取决于”猜测本身的先验概率”和“这个猜测生成我们观测到的数据的可能性大小“。

那么如果用户输入的是tha，那么在巨大的词库中，the和that出现的概率谁会更大一点呢，这里假设是the，那么这里the的先验概率就要比that的先验概率大。

按照贝叶斯的方法计算：P(c)*P(W|c)，P(c)是特定的先验概率。

也就是说，按照上面的例子，用户输入的是tha,当一般的统计无法做出判决时，先验概率这时候就站出来了，它就会根据the的先验概率大，即确定用户想输入的是the。

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！